在海康威视的面试中,对方问了这么一道题:
有一个容量足够大的栈,n个元素以一定的顺序入栈,出栈顺序有多少种?
比如,AB两个元素,入栈顺序为AB,出栈情况有两种:
(1)入A,出A,入B,出B,出栈顺序为AB;
(2)入A,入B,出B,出A,出栈顺序为BA。
因此,2个元素时,结果为2。
分析:设f(n)为“n个元素以一定的顺序入栈,出栈顺序的种类数”。显然f(1)=1,f(2)=2。我们现在来分析一般情况。一般情况下,我们可以按照“第一个入栈的元素,在出栈序列中的位置”作为分类手段。
举个例子,我们假设入栈元素为A,B,C,D。我们按照“A在出栈序列中的位置”分类讨论:
(1)当A第一个出栈时,A先进,然后马上出栈。这种情况下,共有“BCD出栈顺序的种类数”种方案。也就是f(n-1)。
(2)当A第二个出栈时,A先进,B再进,之后B需要马上出来(这样才能确保A排第二)。此时共有f(n-2)种方案。
(3)当A第三个出栈时,A先进,之后只要确保排在A后面两个的元素比A先出即可。此时共有f(2)*f(1)种方案。f(2)是指“BC入栈出栈顺序的种类数”,f(1)是指”D入栈出栈的种类数”。
……
分析到这里,规律就很显然了。
从第一项开始,分别是第一个入栈元素在第i+1个出栈的情况数。
上式中,令f(0)=1 。
这个实际上是卡特兰数(Catalan number,又称卡塔兰数)。
若编程实现,需要维护一个一维数组,时间复杂度为O(n^2)。(递归实现的时间复杂度太高)。
卡塔兰数的通项公式为h(n)=C(2n,n)-C(2n,n+1)(n=0,1,2,...)。







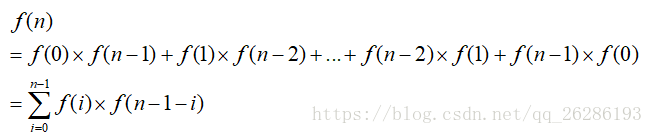













 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








