MATLAB智能算法实现 (一)
写在前面:突然想做点儿什么,为自己本科四年的学习生涯画上一个句点。用一款自己喜欢的软件实现一些老师们在上课时总提到的智能算法应该是一件极有意义的事吧!
我的目的:没什么目的,万一将来用得上呢?!
我的希望:
1、有C语言基础和MATLAB基本矩阵计算实践的童鞋们可以无障碍阅读代码;
2、写这些东西的人不是大神,所以不希望大神前来吐槽。仅供包括我在内的菜鸟们交流讨论;
3、再次强调,大神们总是忘了自己矬的时候是什么样,所以希望诸位大触看看即可,笑笑也罢。
蚁群算法
所有的群智能算法的核心思想都在于:“个体的行为确定了群体的行动模式,个体又接收着来自群体的信息并依据此调整自己的行为”。那么归于蚁群,这一算法的特征有三:
其一,蚂蚁个体在其行动路径上总是均匀地播撒信息素;
其二,信息素的浓度随着时间的变化而变化,同时信息素是蚂蚁个体间极为重要的协调单元;
其三,蚂蚁个体总沿着信息素浓度高的方向前进,但又有一些随机扰动使得其偏离原有的路线。
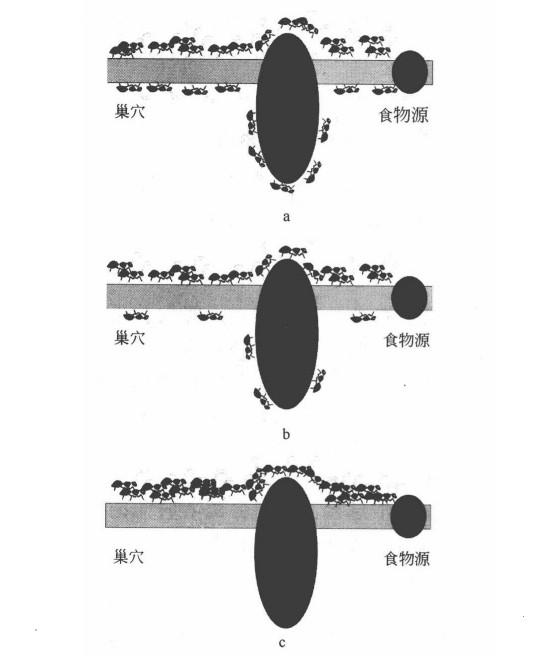
如上图所示,在a时刻,蚂蚁并不知道那条路距离食物更近,于是从巢穴出发的蚂蚁沿着食物发出的“香味”找到上下两条道路。如果我们假定:
1)每只蚂蚁一次出行(往返)所能释放的信息素总量是相同的;
2)蚂蚁们保持相等的时间间隔交替选择出行路线,即t时刻出动的蚂蚁选择上面的道路,t+1时刻出动的就选择下面的道路,t+2时刻又回到上面的道路。
基于以上两条假定,我们可以得出:上面的路径由于距离较短,所以单位长度上的信息素量(浓度)要高于下方路径。所以一段时间过后信息素的浓度差异已经足以引起大多数蚂蚁的关注,上方道路上的蚂蚁开始逐渐变多(b时刻)。
我们可以想到,b状态最终将发展成为c状态,信息素随时间变化浓度降低,有鲜有蚂蚁行至于此,所以下方道路的信息素逐渐消散。同时需要关注的是,有些特立独行的蚂蚁并不以信息素浓度最为自己选择路线的唯一标准,它们会开辟一些新的道路,同时引起一些同伴的关注。这种随机性也为系统的自由化提供了理论基础,这些“创新”的探索如果的确距离更短,那么这一路径将在信息素的调解下演化成为新的主流,反正则会得到纠正。
以下是解放军工程信息大学的一位老师编写的MATLAB程序,它利用蚁群算法,实现了“担货郎”问题的求解(遍历所有的销售点,同时使得总的行进路程最短)。以下是源代码和本人对程序的解释:
function[R_best,L_best,L_ave,Shortest_Route,Shortest_Length] = ACATSP(C,NC_max,m,Alpha,Beta,Rho,Q)
%% 主要符号说明
%% C:n个城市的坐标,n*2的矩阵
%% NC_max:最大迭代次数
%% m:蚂蚁个数
%% Alpha:表征信息素重要程度的参数
%% Beta:表征启发因子重要程度的参数
%% Rho:信息素蒸发系数
%% Q:信息素增加强度系数
%% R_best:各代最佳路线
%% L_best:各代最佳路线长度
%% Step1:变量初始化
n = size(C,1);
% D为一个无向加权图,表中的每一行记录了某一个城市到另外n-1个城市的距离
D = zeros(n,n);
for i = 1:1:n
for j = 1:1:n
if i ~= j
D(i,j) = ((C(i,1) - C(j,1))^2 + (C(i,2) - C(j,2))^2)^0.5;
else
% eps是MATLAB所能识别的最小正浮点数,即认为“0+eps/2 = 0”
D(i,j) = eps;
end
end
end
% Eta表示了距离倒数,作为路径选择重要的启发因子,蚂蚁去信息素多且离当前位置距离较近的城市
Eta = 1./D;
% Tau表示城市间(n*n矩阵)的信息素含量,一开始是均匀的为一个“全一”矩阵
Tau = ones(n,n);
% 每一只蚂蚁都要根据信息素和自己判断,独立求解“担货郎”问题,Tabu记录着m只蚂蚁在n个城市间行进的轨迹。第m行n列表示:第m只蚂蚁去的第n个城市为Tabu(m,n)
Tabu = zeros(m,n);
% NC是迭代次数
NC = 1;
% 每一次迭代结束后的最段路径
R_best = zeros(NC_max,n);
% 每一次迭代后的最短路径长度
L_best = inf.*ones(NC_max,1);
% 每一次迭代后m只蚂蚁所得路径的平均值
L_ave = zeros(NC,1);
while NC <= NC_max
%% Step2:将m只蚂蚁放到n个城市上
RandPosition = [];
% ceil函数是向上取整,randperm函数是生成随机数列,randper(3)就可能是[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]。所以循环m/n次,每一次放n个城市各放一只蚂蚁,最后取前m值蚂蚁(RandPosition(1,1:m))。其意义就在于当m = 2n+1时,我可以保证每个城市至少有两只蚂蚁,且有一只蚂蚁是随机出现在任意城市位置的
for i = 1:(ceil(m/n))
RandPosition = [RandPosition,randperm(n)];
end
% Tabu(:,1)记录着初始状态下m只蚂蚁的位置
Tabu(:,1) = (RandPosition(1,1:m))';
%% Step3:这m只蚂蚁去当前位置之外的其它城市的概率,并依据概率最大的原则选择下一步需要到达的城市
for j = 2:1:n
for i = 1:1:m
% visited是已经走过的城市,J是当前没有走过的城市,P记录着去每一个J中城市的概率
visited = Tabu(i,1:(j-1));
J = zeros(1,(n-j+1));
P = J;
Jc = 1;
% 这个循环就是生成J的过程,就是在visited中寻找,如果找到了某一城市的编号就跳过,如果没有就把它加入J
for k = 1:1:n
if length(find(visited == k)) == 0
J(Jc) = k;
Jc = Jc + 1;
end
end
% 去某一城市的概率既由从当前城市到它的路径上的信息素浓度决定,又与路径的长度相关
for k = 1:1:length(J)
P(k) = (Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);
end
P = P/sum(P);
P_max = P(1);
index = 1;
for l = 1:1:length(P)
if P(l) >= P_max
P_max = P(l);
index = l;
end
end
% 找出其中概率最大的目标城市,并把它放入路径表Tabu
to_visit = J(index);
Tabu(i,j) = to_visit;
end
end
% 当迭代次数大于等于2时,将前一代的最短路径放入Tabu表,进行新一轮的比较,以确保算法的收敛
if NC >= 2
Tabu(i,:) = R_best(NC-1,:);
end
%% Step4:计算要输出参数
L = zeros(m,1);
for i = 1:1:m
R = Tabu(i,:);
for j = 1:1:(n-1)
L(i) = L(i) + D(R(j),R(j+1));
end
% 这里要特别注意要加上从末点到始点的距离,因为蚂蚁要回到原始位置,这样的总的路径长度的比较才有意义,我们也可以由此知道从哪一个城市开始走会得到最优的效果
L(i) = L(i) + D(R(1),R(n));
end
% L_best是当前所有m个路径长度中最小的
L_best(NC) = min(L);
index = find(L == L_best(NC));
% 最短路径要从Tabu表中寻找
R_best(NC,:) = Tabu(index(1),:);
L_ave(NC) = mean(L);
NC = NC + 1;
%% Step5:更新信息素
Delta_Tau = zeros(n,n);
% 每一只蚂蚁单次播撒的信息素量是一定的Q,所以一次遍历之后路径上每两个相邻城市间的信息素浓度增加为Q/L(i)(要注意由于最终要回到原点所以始末两点理论上也是相邻的)
for i = 1:1:m
for j = 1:1:(n-1)
Delta_Tau(Tabu(i,j),Tabu(i,j+1)) = Delta_Tau(Tabu(i,j),Tabu(i,j+1)) + Q/L(i);
end
Delta_Tau(Tabu(i,n),Tabu(i,1)) = Delta_Tau(Tabu(i,n),Tabu(i,1)) + Q/L(i);
end
% Rho是挥发系数,描述了信息素浓度的降低速度
Tau = (1-Rho).*Tau + Delta_Tau;
Tabu = zeros(m,n);
end
% Step6:图形输出
Pos = find(L_best == min(L_best));
Shortest_Route = R_best(Pos(1),:);
Shortest_Length = L_best(Pos(1));
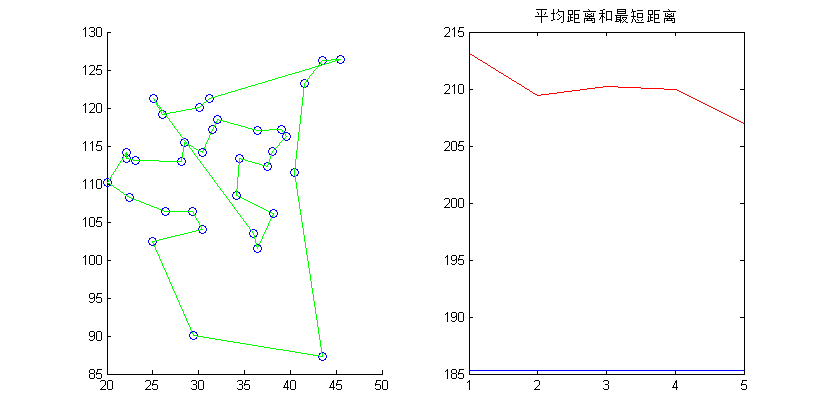
% 左边的图表示在二维空间上NC次迭代后最短路径的分布,右边的图有两个部分,其一是平均距离的变化,其二是最短距离的变化。算法中的DrawRoute是一个自定义函数,在附件当中这里就不加解释
subplot(1,2,1);
DrawRoute(C,Shortest_Route);
subplot(1,2,2);
plot(L_best);
hold on;
plot(L_ave,'r');
title('平均距离和最短距离');function DrawRoute(C,R)
%%=========================================================================
%% DrawRoute.m
%% 画路线图的子函数
%%-------------------------------------------------------------------------
%% C Coordinate 节点坐标,由一个N×2的矩阵存储
%% R Route 路线
%%=========================================================================
N=length(R);
scatter(C(:,1),C(:,2));
hold on
plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')
hold on
for ii=2:N
plot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g')
hold on
end将中国全部省会城市的经纬度坐标输入成为一个35*2的矩阵,作为函数的C参数。设定10次迭代,150只蚂蚁,信息素与路径长度的启发因子相同即Alpha = Beta = 0.5,信息素挥发系数为0.2,单次播撒信息素的量为1。可得到如下的结果图。
在编写注释过程中可能会造成代码无法正常运行,如有错误,望告知!






















 598
598











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








