数据结构与算法小结（1）

一、概述

数据结构，即数据存放的方式。算法，解决问题的方法。讨论数据结构与算法时，常常不会仅仅满足于能解决一个特定的问题，而是在追求如何优雅而高效的解决一类问题。
本文针对学堂在线的数据结构课程的小结，用以巩固知识点。课程主要介绍的是向量、链表、BST、堆等数据结构的特点以及在这些数据中存储、访问数据的具体的、不同的实现算法的比较，其中有大量的实例和具体的数据变换时数据结构的状态，便于理解。

二、算法好坏的评判

1. 算法的定义
   特定计算模型下，旨在解决特定问题的指令序列，需具备的特性：

   a.正确性：的确可以解决指定的问题。  //得到正确的结果
   b.确定性：任一算法都可以描述为一个由基本操作组成的序列    //可以被转化为具体的操作步骤，且无二义性
   c.可行性：每一基本操作都可实现，且在常数时间内完成。
   d.有穷性：对于任何输入，经有穷次基本操作，都可以得到输出
   

   具备以上特性，只能说是一个算法，而好算法，还需要满足这些要求：

   A.正确：能正确处理简单的、大规模的、一般的、退化的（平凡的，即特例）、任意合法的输入
   B.健壮：能辨别不合法的输入并做适当处理    //任意非法输入
   C.可读：命名、注释、统一风格   //便于理解和维护
   

2. 算法优劣的评判
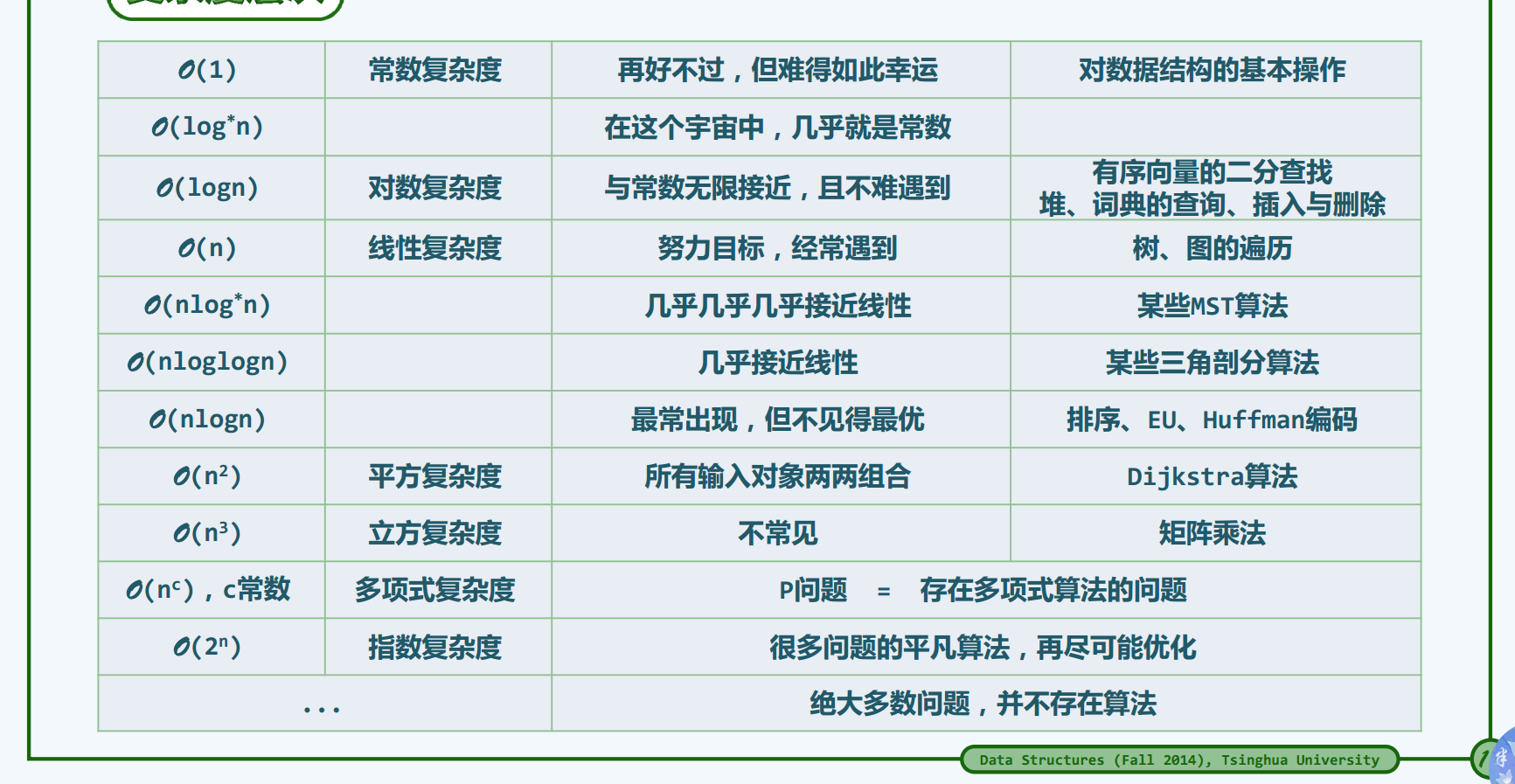
   渐进分析：大O记号，忽略常数，更关心输入足够大后的成本，注重考察成本的增长趋势。

   
   

   注意，有些特殊的算法在渐进意义上可以让人满意，但实际在使用时，由于被忽略的常数项太大、访问内存地址非连续而导致无法利用CPU的高速缓存特性等原因，表现的效果与渐进分析结果相差很大，所以需在此特别指出，渐进分析只是一种主要的分析工具，但它不是评判算法好坏的硬性标准，需以具体算法在应用中的实际表现为准。

3. 算法正确性的证明：
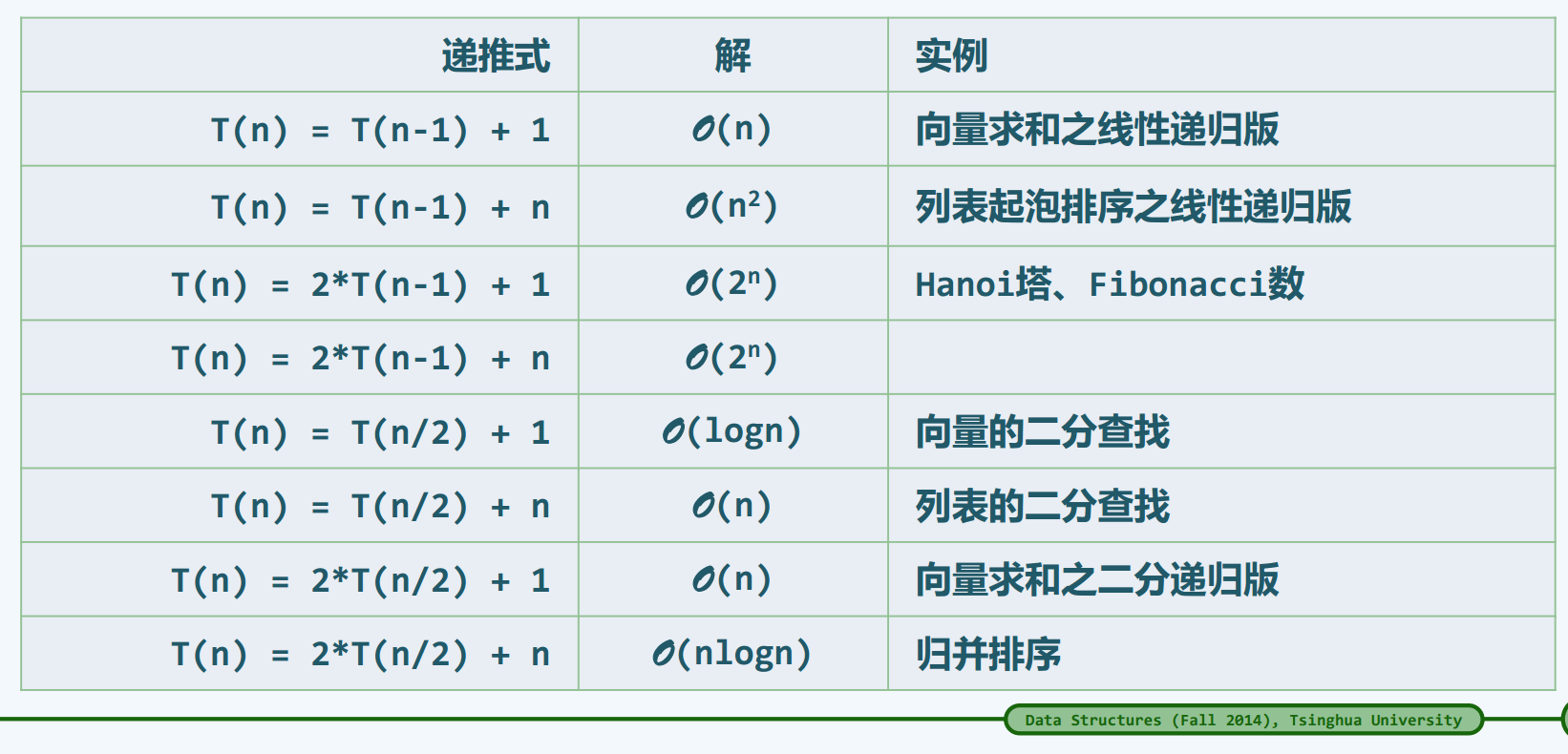
   类似递归，由算法的不变性（处理方式固定） 和单调性（规模不断缩减），最终得到算法的正确性。

4. 递归到迭代的转换：
   a. 记忆：将已计算过的实例的结果制表备查
   b. 动态规划：颠倒计算方向，有自顶而下的递归，改为自底而上的迭代。

三、向量

1. 向量，是数组的抽象与泛化，由一组元素按线性次序封装而成。

2. 相关概念：

   输入敏感：对于不同的输入，算法所需时间相差很大，比如，对于无序向量的顺序查找操作，最好需要O(1)常数，最差需要O(n)线性。
   
   有序性和无序性：是否存在相邻的逆序对。而相邻逆序对的数量可用于度量向量的逆序程度。
   
   判等器：比较元素之间是否相等。
   比较器：比较不同元素在逻辑上的大小关系。
   无序向量可以只有判等器，而没有比较器；有序向量必须两者都有。所谓有序的序，就是由比较器比较得到的顺序。
   
   排序算法的稳定性：针对含有重复元素的向量而言的。所谓的稳定，就是相同的元素在排序前后的，它们之间的次序保持不变。
   

3. 得到的启发：

   在有序向量的去重（唯一化）算法中，其最终算法简述如下：维持两个指针，一个指针j用于遍历向量，另一个记录应该保留的元素，当找到每一块重复区域中的第一个元素，即一个新的不重复元素时，arr[i++] = arr[j],若元素存在arr[j]==arr[i],则i不变j++，最后将向量长度调整为i即可。这种覆盖无效元素处理方式，在时间和空间上都是高效的，值得借鉴。

四、列表

根据是否修改的数据结构，所有的操作大致分为两类方式

静态：仅读取，数据结构的内容及组成一般不变。类似于http的get操作，重复多次操作得到的结果相同。
动态：需写入，数据结构的局部或整体将改变。类似于http协议中的post、remove等非幂等的操作。

对应的数据元素的存储与组织方式也分为两种

静态：通过物理内存的位置来体现数据的层级关系。如数组，左式堆等。
动态：物理位置任意，数据的层级关系由与数据绑定存储的额外信息提供，如链表，二叉树等。每个元素都会维护相应的引用，指向与其有关联的元素所在存储位置。

列表的相关概念

头、首、末、尾节点，其秩可理解为：-1、0、n-1、n。
    头尾哨兵的引用，使列表首节点前、末节点后插入元素以及查找元素等处的处理变得简单。
前驱为元素指向前一个节点的引用，后继为元素指向后一个节点的引用。进行插入、删除元素等动态操作时，需同步维护相邻元素的前驱、后继。

补充

在不支持指针的语言中实现列表的方法：
    两个数组，一个为elem[]保存数据，另一个在秩相同的位置保存后继元素的秩（实现对后继的引用），需对外提供首节点的秩。

五、栈

操作

压栈 push
弹出 pop
查顶 top
栈深度 size

特点

先进后出（FILO）

实现

以向量来实现，并以向量末端为栈顶。如此实现比以向量首端为栈顶或列表的实现，效率更高。

应用

1. 逆序输出
   短除法，结果存入栈中，最后逆序输出

   void convert(Stack<char> &s, _int64 n, int base){   //base 待转进制
       static char digit[] = {'0','1','2','3','4','5','6','7'};
       while(n > 0){
           s.push(digit[n % base]);
           n /= base;
       }
   }
   

2. 递归嵌套
   以括号匹配为例，采用减而治之或分而治之。需要分解之前的情况为分解之后情况的必要条件，而非充分条件。即，可以由分解后的情况并不是唯一可以推出分解前情况的解。
   重要条件：减去紧邻的括号
   使用栈来实现：

   bool paren(const char exp[],int lo,int hi){  //exp中只存有左右括号。
       Stack<char> s;
       for(int i = lo;i < hi;i++){
           if('(' == exp[i]){s.push(exp[i]);}
           else if(!s.empty()){s.pop();}
           else{return false;}
       }
       return s.empty();
   }
   计数器也可实现上述功能。+/-
   但存在多个括号，如“[(])”时，因为不能嵌套使用括号，所以使用栈，而计数器将无效。
   可由此推广到html标签的嵌套检查。
   

   栈混洗：stack permutation
   [栈底，栈顶>
   长度为n的序列，可能的栈混洗总数：(sp(n)<=n!全排列);
   推导步骤：1号元素作为第k个元素推入栈中时的总数：
   sp(k-1)*sp(n-k)
   对上式从1到n（k可能的取值）求和，得总数为catalan(n) = (2*n)!/(n+1)!/n!。

   栈混洗的甄别：
   任意三个元素能否按某相对次序出现于混洗中，与其他元素无关。
   充要条件：对于任何1<=i < j < k <= n, k,i,j必然非栈混洗 （禁形，“3,1,2”必定无法洗出）

   甄别算法一：
       任意i<j,不含j+1,i,j模式，即为合适的栈混洗(n^2)
   甄别算法二：
       直接借助栈A，B，S模拟栈混洗过程
           pop前检测S是否为空；或需弹出的元素在S中，却非顶元素
   n的元素对应的栈混洗有多少种，n对括号对应的合法表达式就有多少种。
   

3. 延迟缓冲
   线性扫描，预读。

   liunx:
       $echo $(表达式)
   dos：
       set /a 表达式
       表达式：(!0 ^<^< (1-2+3*4)) -5 *(6^|7)/(8^^9)
   

4. 栈式计算
   中缀表达式的计算：
   核心是将数值压入栈，将操作符压入另一个栈，根据栈顶的操作符与当前待压入栈中的操作符的关系（如下图），决定处理当前操作符，还是压入、弹出栈顶操作符并运算，知道当前操作符可以入栈。
   

逆波兰表达式（RPN，后缀表达式）的计算：

特点：不使用括号，即可表示优先级的运算关系。（但需引入另一个原字符，用于分隔相邻的数值）
    只使用一个栈来求值，从左向右扫描表达式，当遇到数值时压入栈中，当遇到操作符时，取出相应的数值，运算后再次压入栈中。

中缀表达式到后缀表达式的转换：
1.用括号显式地表示优先级
2.将运算符移到对应的括号后，
3.抹去所有的括号

六、树

1. 相关概念

    图论中得到的结论：
    树：无环连通图、极小连通图、极大无环图

    任意节点通往根的路径是唯一的。节点v ---- 路径v到根的路径 ---- 以节点为根的子树  （唯一的）
    每个节点的直接孩子个数即为该节点的出度数之和，所有节点的出度数之和为n-1，即总边数。n为节点总数

    半线性：祖先若存在，则必然唯一；后代若存在，则未必唯一。
    根节点：所有节点的公共祖先，深度为0。
    叶子：没有后代的节点称为叶子。
    树的高度：所有叶子深度中的最大者为树的高度。空树高度为-1.

    树的参考实现，使用链表数据结构（考虑查找、增加、删除的效率），
    每个节点中维护的引用关系由如下方式表示：
        父亲孩子法：
            序号 | 节点数据 | 父节点序号 | 子节点列表集
        长子兄弟法（主要）：
            序号 | 节点数据 | 父节点 | 第一个子节点 | 下一个兄弟节点
    整个树结构需维护的信息：
        树的高度：增删时需更新树高。

    二叉树：
        非叶子节点度数不大于2

    真二叉树：
        每个节点的出度为偶数

    二叉树可以表示所有有根有序的树：
        长子--左节点
        兄弟--右节点

    完全二叉树：
    叶节点：仅限于最低两层，底层叶子均居于次底层叶子左侧；除末节点的父亲，内部节点均有双子。叶节点不少于内部节点的个数，但最多多出一个。

2. 树的遍历

先序、中序、后序遍历：以树根节点的位置区分，递归遍历。三种遍历都有后代先于祖先被访问，即，存在逆序的，所以需借助栈结构来实现遍历操作

先序遍历的递归实现：（根节点|左子树|右子树）
    方法一，栈结构，根元素先入栈，后进行循环，每次循环弹出栈顶并访问，同时若有右孩子则将其，再判断若有左孩子，有也将其压栈并进入下一个循环，直到栈空。（要先左后右，在压栈时就要相反）
    方法二，栈结构，不断沿左侧链访问，并将右子树的根节点入栈；当访问元素为空时（一条左侧链访问完毕），从栈中弹出一个节点，同样沿着左侧链访问并将右子树压入同一个栈，循环至栈空。

中序遍历的递归实现：（左子树|根节点|右子树）
    栈结构，【沿根节点将所有左侧链的元素压入栈中，弹出栈顶并访问，转向其右孩子】，重复【】内的操作直至栈空

后序遍历的递归实现：（左子树|右子树|根节点）
    栈结构，根节点入栈，【检查栈顶元素，若有左孩子，1.当左孩子（lc）还有右孩子（lc-rc）时，右孩子（lc-rc）入栈，然后才是左孩子（lc）,2.当左孩子（lc）没有右孩子（lc-rc）时，直接入栈；若栈顶元素没有左孩子时，栈顶元素的右孩子（rc）入栈，若右孩子（rc）也没有，表明到达叶节点，弹出栈顶元素并访问】，检查栈顶元素，若为上一个访问元素的父亲，则可直接访问，否则必为其右兄，重复【】。

层次遍历：按树的深度访问
    祖先节点必定先于后代访问，即，顺序访问（自上而下，先左后右），借助队列结构实现
    根节点入队，循环取出首节点，访问并将其左右节点顺序放入队列尾部，直至队空。

七、图

1. 基本概念

邻接：同一条边的两个顶点，彼此邻接。
自环：同一顶点自我邻接，为自环。
简单图：不含自环的图，主要考察的对象。
关联：顶点与其所属的边彼此关联。
度：与同一顶点关联的边数。出入度，表示由顶点出、或指向顶点。
无向边：边的两个顶点无次序。根据组成图的边有无向可将图分为无向图、有向图、混合图。
有向图可以表示无向图和混合图：一条无向边可看做正反两条有向边。
DAG：有向无环图

欧拉环路：各边各出现一次。
哈密尔顿环路：各顶点各出现一次。
平面图：可嵌于平面的图。各边互不相交。
    平面图的本质：任意平面图满足欧拉公式
        v - e + f - c = 1
        v：0维的元素，顶点
        e：1维的元素，边
        f：2维的元素，区域面片
        c：连通域的总数
    对于平面图：e<=3*n-6 = o(n) << n^2
        边的总数不可能超过顶点的总数

支撑树：也称生成树(spanning tree)，以无向图为研究对象。以某一节点为根，通过裁剪部分边，得到一棵树，通过该树，可以遍历所有的节点。特点：每对节点之间的只有唯一的路径，支撑并不唯一。当无向图的每条边都附带权重时，若得到的支撑树的所有路径权重之和最小（与该无向图的其他支撑树相比），则称其为最小支撑树。实际应用：网络中的路由计算。

连通图：无向图中，任意两个顶点之间都有路径，则称为连通图。
连通域：从一个节点可以通过遍历到达的所有区域。一个图可能不只一个连通域
连通分量：无向图的极大连通子图称为G的连通分量。
    连通图的连通分量为其自身。非连通图的连通分量有多个，每个极大的连通子图即为一个连通分量。
可达分量：与连通分量类似，可达分量用于描述有向图。自一个顶点通过有向图可以达到的极大子图即为一个可达分量。

遍历：
    将图变为树。
    将数变为线性表。

2. 图的表示

邻接矩阵：
    顶点个数*顶点个数的二维矩阵，如若（u, v）有向边存在，则将第u行第v列置1，否则置0。
    适用：经常检测边的存在、做边的插入删除操作、稠密图、图规模固定（顶点树固定）
关联矩阵：
    顶点个数*边的个数的二维矩阵，若顶点与边关联，则置1，否则置0.

邻接表：使用数组存储顶点，每个顶点维持一个列表，只存储存在的边（存储边的另一个关联顶点即可）
    适用：经常计算顶点的度数、遍历、稀疏图、顶点数目不固定。

3. 图的遍历：

广度优先搜索BFS：

-> 从一个节点开始，一次访问所有尚未访问的邻接顶点，再循环访问直至完成。
-> 使用队列实现，等同于树的广度优先遍历。最后会得到一颗支撑树。
-> 遍历所有的顶点，若未被访问，则从其开始做BFS搜索。直到所有顶点被访问。最后可能有多颗树。
-> 边的分类，一个顶点访问后，找到一条未发现的边，若边的另一个邻接顶点标记为未访问，则将该边置为树边（在最后支撑树种存在的边），否则若为已访问，则将该边标记为跨边（不会再最后的支撑树中出现）。
->一个连通/可达分量会得到一个支撑树。

深度优先搜索DFS：

自顶点起，若有尚未访问的顶点，则任取其一，递归执行DFS，否则返回。
最初顶点状态初始化为undiscovered,从某一顶点刚进入DFS时，设置dTime以及状态为discovered，表示开始访问时间，当找不到未访问顶点时，在退出DFS之前设置fTime以及装填visited，表示访问结束时间。
根据边关联的顶点状态判断并标识边：当前顶点状态一定为discovered）
    当前顶点 ---> undiscovered    树边
    当前顶点 ---> discovered      后向边（回路）
    当前顶点 ---> visited （当前顶点更早被发现）        前向边（只在有向图中出现）
    当前顶点 ---> visited  (当前顶点较晚发现)   跨边
等效于树的先序遍历，最后也会得到一颗支撑树。
括号引理：
    顶点活跃期：fTime - dTime
    一个顶点u为另一个顶点v的祖先，当且仅当u的活跃期包含v的活跃期。
    u与v无关当且仅当两者活跃期无交集。
    原因：使用递归，dTime、fTime的设置分别在递归的开始和结尾。