| 本文转载自http://f.dataguru.cn/thread-460065-1-1.html,仅用作个人学习。 0 引言 11月1日上午,机器学习班第7次课,邹博讲聚类(PPT),其中的谱聚类引起了自己的兴趣,他从最基本的概念:单位向量、两个向量的正交、方阵的特征值和特征向量,讲到相似度图、拉普拉斯矩阵,最后讲谱聚类的目标函数和其算法流程。 课后自己又琢磨了番谱聚类跟拉普拉斯矩阵,打算写篇博客记录学习心得, 若有不足或建议,欢迎随时不吝指出,thanks。
1 矩阵基础 在讲谱聚类之前,有必要了解一些矩阵方面的基础知识。 1.0 理解矩阵的12点数学笔记 如果对矩阵的概念已经模糊,推荐国内一人写的《理解矩阵by孟岩》系列,其中,抛出了很多有趣的观点,我之前在阅读的过程中做了些笔记,如下:
“1、简而言之:矩阵是线性空间里的变换的描述,相似矩阵则是对同一个线性变换的不同描述。那,何谓空间?本质而言,“空间是容纳运动的一个对象集合,而变换则规定了对应空间的运动”by孟岩。在线性空间选定基后,向量刻画对象的运动,运动则通过矩阵与向量相乘来施加。然,到底什么是基?坐标系也。 2、有了基,那么在(1)中所言的则应是:矩阵是线性空间里的变换的描述,相似矩阵则是对同一个线性变换在不同基(坐标系)下的不同描述。出来了两个问题,一者何谓变换,二者不同基(坐标系)如何理解?事实上,所谓变换,即空间里从一个点(元素/对象)到另一个(元素对象)的跃迁,矩阵用来描述线性变换。基呢?通过前面已知,矩阵无非不过就是用来描述线性空间中的线性变换的一个东西而已,线性变换为名词,矩阵为描述它的形容词,正如描述同一个人长得好看可以用多个不同形容词"帅”"靓”描述,同一个线性变换也可以由多个不同的矩阵来描述,而由哪一个矩阵描述它,则由基(坐标系)确定。
3、前面说了基,坐标系也,形象表述则为角度,看一个问题的角度不同,描述问题得到的结论也不同,但结论不代表问题本身,同理,对于一个线性变换,可以选定一组基,得到一个矩阵描述它,换一组基,得到不同矩阵描述它,矩阵只是描述线性变换非线性变换本身,类比给一个人选取不同角度拍照。
4、前面都是说矩阵描述线性变换,然,矩阵不仅可以用来描述线性变换,更可以用来描述基(坐标系/角度),前者好理解,无非是通过变换的矩阵把线性空间中的一个点给变换到另一个点上去,但你说矩阵用来描述基(把一个坐标系变换到另一个坐标系),这可又是何意呢?实际上,变换点与变换坐标系,异曲同工!
(@坎儿井围脖:矩阵还可以用来描述微分和积分变换。关键看基代表什么,用坐标基就是坐标变换。如果基是小波基或傅里叶基,就可以用来描述小波变换或傅里叶变换)
5、矩阵是线性运动(变换)的描述,矩阵与向量相乘则是实施运动(变换)的过程,同一个变换在不同的坐标系下表现为不同的矩阵,但本质/征值相同,运动是相对的,对象的变换等价于坐标系的变换,如点(1,1)变到(2,3),一者可以让坐标点移动,二者可以让X轴单位度量长度变成原来1/2,让Y轴单位度量长度变成原来1/3,前后两者都可以达到目的。
6、Ma=b,坐标点移动则是向量a经过矩阵M所描述的变换,变成了向量b;变坐标系则是有一个向量,它在坐标系M的度量下结果为a,在坐标系I(I为单位矩阵,主对角为1,其它为0)的度量下结果为b,本质上点运动与变换坐标系两者等价。为何?如(5)所述,同一个变换,不同坐标系下表现不同矩阵,但本质相同。
7、Ib,I在(6)中说为单位坐标系,其实就是我们常说的直角坐标系,如Ma=Ib,在M坐标系里是向量a,在I坐标系里是向量b,本质上就是同一个向量,故此谓矩阵乘法计算无异于身份识别。且慢,什么是向量?放在坐标系中度量,后把度量的结果(向量在各个坐标轴上投影值)按顺序排列在一起,即成向量。
8、b在I坐标系中则是Ib,a在M坐标系中则是Ma,故而矩阵乘法MxN,不过是N在M坐标系中度量得到MN,而M本身在I坐标系中度量出。故Ma=Ib,M坐标系中的a转过来在I坐标系中一量,却成了b。如向量(x,y)在单位长度均为1的直角坐标系中一量,是(1,1),而在X轴单位长度为2.Y轴单位长度为3一量则是(2,3)。
9、何谓逆矩阵? Ma=Ib,之前已明了坐标点变换a-〉b等价于坐标系变换M-〉I,但具体M如何变为I呢,答曰让M乘以M的逆矩阵。以坐标系
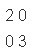
为例,X轴单位度量长度变为原来的1/2,Y轴单位度量长度变为原来的1/3,即与矩阵

相乘,便成直角坐标系I。即对坐标系施加变换,即让其与变换矩阵相乘。 ”
1.1 一堆基础概念 根据wikipedia的介绍,在矩阵中,file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/5%60S)DX12(%7D%7BQTLL7TF35%7B%7D7.tmpn阶单位矩阵,是一个file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/L7@R@%7B21PKAA3Z~382Z%7DTC9.tmp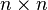 的方形矩阵,其主对角线元素为1,其余元素为0。单位矩阵以file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/G_KDERTC2%605UR$)RC%60]%60NKU.tmp 的方形矩阵,其主对角线元素为1,其余元素为0。单位矩阵以file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/G_KDERTC2%605UR$)RC%60]%60NKU.tmp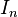 表示;如果阶数可忽略,或可由前后文确定的话,也可简记为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/VZDW9_F46YVMR_VM)VA]ERR.tmp 表示;如果阶数可忽略,或可由前后文确定的话,也可简记为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/VZDW9_F46YVMR_VM)VA]ERR.tmp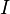 (或者E)。 如下图所示,便是一些单位矩阵: (或者E)。 如下图所示,便是一些单位矩阵:
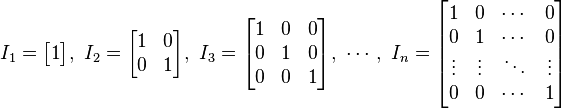
单位矩阵中的第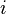 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/KCGF~5Q(I40%60UG0OIGKD%60UD.tmp列即为单位向量 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/KCGF~5Q(I40%60UG0OIGKD%60UD.tmp列即为单位向量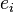 file:///http://upload.wikimedia.org/math/f/9/a/f9a6812140bf479d2171492563c09cfd.png。单位向量同时也是单位矩阵的特征向量,特征值皆为1,因此这是唯一的特征值,且具有重数n。由此可见,单位矩阵的行列式为1,且迹数为file:///http://upload.wikimedia.org/math/7/b/8/7b8b965ad4bca0e41ab51de7b31363a1.pngn。 file:///http://upload.wikimedia.org/math/f/9/a/f9a6812140bf479d2171492563c09cfd.png。单位向量同时也是单位矩阵的特征向量,特征值皆为1,因此这是唯一的特征值,且具有重数n。由此可见,单位矩阵的行列式为1,且迹数为file:///http://upload.wikimedia.org/math/7/b/8/7b8b965ad4bca0e41ab51de7b31363a1.pngn。
单位向量又是什么呢?数学上,赋范向量空间中的单位向量就是长度为 1 的向量。欧几里得空间中,两个单位向量的点积就是它们之间角度的余弦(因为它们的长度都是 1)。
一个非零向量 的正规化向量(即单位向量) 的正规化向量(即单位向量)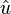 就是平行于 就是平行于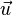 的单位向量,记作: 的单位向量,记作:
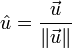
file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/OM5SBIB$Y%7B9$W46K])2FNPH.tmp
这里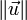 是 是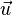 的范数(长度)。 的范数(长度)。
何谓点积?点积又称内积,两个向量file:///http://upload.wikimedia.org/math/a/1/5/a159b61a2221d23bb55d352231cab456.png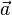 = [a1, a2,…, an]和[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7DK1K)PWO%7D7M_[$F~G[GKT9.tmp[/img] = [a1, a2,…, an]和[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7DK1K)PWO%7D7M_[$F~G[GKT9.tmp[/img]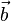 = [b1, b2,…, bn]的点积定义为: = [b1, b2,…, bn]的点积定义为:
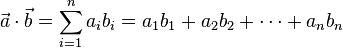
这里的Σ指示求和符号。
例如,两个三维向量[1, 3, -5]和[4, -2, -1]的点积是file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/01%7BD%60C)N%60NT8RN]9M(%60_IEN.tmp:
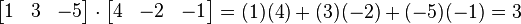
使用矩阵乘法并把(纵列)向量当作n×1 矩阵,点积还可以写为:
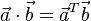
这里的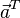 file:///http://upload.wikimedia.org/math/4/1/7/417ed20e95388353a9463fba7b95ac17.png指示矩阵file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/ZDJ%7B2@4C@XTSMFIU2DW%L9K.tmp的转置。使用上面的例子,将一个1×3矩阵(就是行向量)乘以一个3×1向量得到结果(通过矩阵乘法的优势得到1×1矩阵也就是标量): file:///http://upload.wikimedia.org/math/4/1/7/417ed20e95388353a9463fba7b95ac17.png指示矩阵file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/ZDJ%7B2@4C@XTSMFIU2DW%L9K.tmp的转置。使用上面的例子,将一个1×3矩阵(就是行向量)乘以一个3×1向量得到结果(通过矩阵乘法的优势得到1×1矩阵也就是标量):
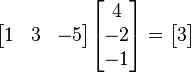
除了上面的代数定义外,点积还有另外一种定义:几何定义。在欧几里得空间中,点积可以直观地定义为file:///http://upload.wikimedia.org/math/0/9/2/09243eaabd696902d133dd2d12eaab76.png:
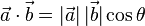
这里|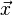 |file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/C]JUJ9JTPHRGF%60CYS%NDO$7.tmp表示[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/K2Z9R]%XFS%7DWWGB[)%7B((RPP.tmp[/img] |file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/C]JUJ9JTPHRGF%60CYS%NDO$7.tmp表示[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/K2Z9R]%XFS%7DWWGB[)%7B((RPP.tmp[/img]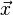 的模(长度),θ表示两个向量之间的角度。 根据这个定义式可得:两个互相垂直的向量的点积总是零。若file:///http://upload.wikimedia.org/math/a/1/5/a159b61a2221d23bb55d352231cab456.png和file:///http://upload.wikimedia.org/math/0/0/5/00534a7a980de9db23c1bdf9cdbde215.png都是单位向量(长度为1),它们的点积就是它们的夹角的余弦。 的模(长度),θ表示两个向量之间的角度。 根据这个定义式可得:两个互相垂直的向量的点积总是零。若file:///http://upload.wikimedia.org/math/a/1/5/a159b61a2221d23bb55d352231cab456.png和file:///http://upload.wikimedia.org/math/0/0/5/00534a7a980de9db23c1bdf9cdbde215.png都是单位向量(长度为1),它们的点积就是它们的夹角的余弦。 正交是垂直这一直观概念的推广,若内积空间中两向量的内积(即点积)为0,则称它们是正交的,相当于这两向量垂直,换言之,如果能够定义向量间的夹角,则正交可以直观的理解为垂直。而正交矩阵(orthogonal matrix)是一个元素为实数,而且行与列皆为正交的单位向量的方块矩阵(方块矩阵,或简称方阵,是行数及列数皆相同的矩阵。)
若数字 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/B)4BU]3RZT8USPGGC%60@KS33.tmp[/img]和非零向量 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/B)4BU]3RZT8USPGGC%60@KS33.tmp[/img]和非零向量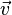 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/H%606(4A[)N52%J_%7D%7B@N]KP$N.tmp[/img]满足file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/EZ(LQ27(70ISGRB%7BBRRYPIR.tmp [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/H%606(4A[)N52%J_%7D%7B@N]KP$N.tmp[/img]满足file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/EZ(LQ27(70ISGRB%7BBRRYPIR.tmp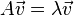 ,则 ,则 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/JQ2GJ%HE9X@FAX)_V_L9_8L.tmp为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/HY3TPN8WYCL8%7D(8M8(G4_H9.tmp file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/JQ2GJ%HE9X@FAX)_V_L9_8L.tmp为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/HY3TPN8WYCL8%7D(8M8(G4_H9.tmp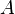 的一个特征向量, 的一个特征向量,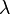 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7$VO8M%7BQ89GTP@@QHLIX9DN.tmp是其对应的特征值。 换句话说,在 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7$VO8M%7BQ89GTP@@QHLIX9DN.tmp是其对应的特征值。 换句话说,在 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/A0TR%7BFU[MG@QG6@KM@XPXZU.tmp[/img]这个方向上, [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/A0TR%7BFU[MG@QG6@KM@XPXZU.tmp[/img]这个方向上,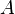 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/P5%60HJ%60HQFLMS1M%60I94%60PP(C.tmp做的事情无非是把[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/P%R[%7B%7B9D%601VCMUI(7UI@4MW.tmp[/img] file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/P5%60HJ%60HQFLMS1M%60I94%60PP(C.tmp做的事情无非是把[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/P%R[%7B%7B9D%601VCMUI(7UI@4MW.tmp[/img] 沿其 沿其 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/8YCLBJ0PGHUI2JC(5IH23)H.tmp的方向拉长/缩短了一点(而不是毫无规律的多维变换), file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/8YCLBJ0PGHUI2JC(5IH23)H.tmp的方向拉长/缩短了一点(而不是毫无规律的多维变换), file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/J~Y~WD_8(R5$1A@%60$DXRD5R.tmp则是表示沿着这个方向上拉伸了多少的比例。 简言之, file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/J~Y~WD_8(R5$1A@%60$DXRD5R.tmp则是表示沿着这个方向上拉伸了多少的比例。 简言之,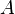 对 对 做了手脚,使得向量 做了手脚,使得向量 变长或变短了,但 变长或变短了,但 本身的方向不变。 本身的方向不变。
矩阵的迹是file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/CV5K11~U~Z$C6~_C6SDJ5(K.tmp矩阵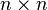 的对角线元素之和,也是其 的对角线元素之和,也是其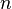 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/E@R4H5F7X[JD16(FE[QJ%7BDS.tmp[/img]个特征值之和。 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/E@R4H5F7X[JD16(FE[QJ%7BDS.tmp[/img]个特征值之和。
更多矩阵相关的概念可以查阅相关wikipedia,或《矩阵分析与应用》。
2 拉普拉斯矩阵2.1 Laplacian matrix的定义 拉普拉斯矩阵(Laplacian matrix)),也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图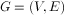 ,其拉普拉斯矩阵被定义为: ,其拉普拉斯矩阵被定义为:
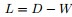
其中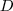 为图的度矩阵, 为图的度矩阵,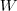 为图的邻接矩阵。 为图的邻接矩阵。
举个例子。给定一个简单的图,如下:
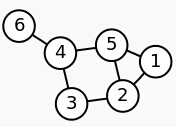
把此“图”转换为邻接矩阵的形式,记为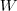 : :

把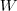 的每一列元素加起来得到 的每一列元素加起来得到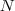 个数,然后把它们放在对角线上(其它地方都是零),组成一个 个数,然后把它们放在对角线上(其它地方都是零),组成一个 的对角矩阵,记为度矩阵 的对角矩阵,记为度矩阵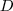 ,如下图所示: ,如下图所示:

根据拉普拉斯矩阵的定义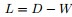 ,可得拉普拉斯矩阵 ,可得拉普拉斯矩阵 为: 为:

2.2 拉普拉斯矩阵的性质 介绍 拉普拉斯矩阵的性质之前,首先定义两个概念,如下:
①对于邻接矩阵,定义图中A子图与B子图之间所有边的权值之和如下:
其中,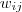 定义为节点 定义为节点 到节点 到节点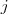 的权值,如果两个节点不是相连的,权值为零。 的权值,如果两个节点不是相连的,权值为零。
②与某结点邻接的所有边的权值和定义为该顶点的度d,多个d 形成一个度矩阵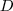 (对角阵) (对角阵)
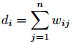
属性: 1.拉普拉斯矩阵是半正定矩阵。 2.特征值中0出现的次数就是图连通区域的个数。 3.最小特征值永远是0,因为每个拉普拉斯矩阵对应特征向量[1,1,1,1,...,1]Lv=0. 4.最小的非0特征值称为谱隙spectral gap. 5. 6.最小非零特征值是图的代数连通度。
拉普拉斯矩阵 具有如下性质: 具有如下性质:
-
 是对称半正定矩阵; 是对称半正定矩阵; -
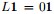 ,即 ,即 的最小特征值是0,相应的特征向量是 的最小特征值是0,相应的特征向量是 。证明: 。证明: * *  = ( = ( - -  ) * ) *  = 0 = 0 * = 0 = 0 *  。(此外,别忘了,之前特征值和特征向量的定义:若数字 。(此外,别忘了,之前特征值和特征向量的定义:若数字 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/B)4BU]3RZT8USPGGC%60@KS33.tmp[/img]和非零向量 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/B)4BU]3RZT8USPGGC%60@KS33.tmp[/img]和非零向量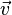 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/H%606(4A[)N52%J_%7D%7B@N]KP$N.tmp[/img]满足file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/EZ(LQ27(70ISGRB%7BBRRYPIR.tmp [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/H%606(4A[)N52%J_%7D%7B@N]KP$N.tmp[/img]满足file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/EZ(LQ27(70ISGRB%7BBRRYPIR.tmp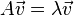 ,则 ,则 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/JQ2GJ%HE9X@FAX)_V_L9_8L.tmp为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/HY3TPN8WYCL8%7D(8M8(G4_H9.tmp file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/JQ2GJ%HE9X@FAX)_V_L9_8L.tmp为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/HY3TPN8WYCL8%7D(8M8(G4_H9.tmp 的一个特征向量, 的一个特征向量, file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7$VO8M%7BQ89GTP@@QHLIX9DN.tmp是其对应的特征值)。 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7$VO8M%7BQ89GTP@@QHLIX9DN.tmp是其对应的特征值)。 -
 有n个非负实特征值 有n个非负实特征值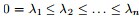 - 且对于任何一个属于实向量
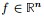 ,有以下式子成立 ,有以下式子成立
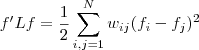
其中,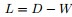 , ,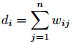 , ,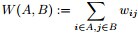 。 。
下面,来证明下上述结论,如下:
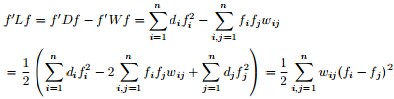
3 谱聚类 所谓聚类(Clustering),就是要把一堆样本合理地分成两份或者K份。从图论的角度来说,聚类的问题就相当于一个图的分割问题。即给定一个图G = (V, E),顶点集V表示各个样本,带权的边表示各个样本之间的相似度,谱聚类的目的便是要找到一种合理的分割图的方法,使得分割后形成若干个子图,连接不同子图的边的权重(相似度)尽可能低,同子图内的边的权重(相似度)尽可能高。物以类聚,人以群分,相似的在一块儿,不相似的彼此远离。
至于如何把图的顶点集分割/切割为不相交的子图有多种办法,如
- cut/Ratio Cut
- Normalized Cut
- 不基于图,而是转换成SVD能解的问题
目的是为了要让被割掉各边的权值和最小,因为被砍掉的边的权值和越小,代表被它们连接的子图之间的相似度越小,隔得越远,而相似度低的子图正好可以从中一刀切断。
本文重点阐述上述的第一种方法,简单提一下第二种,第三种本文不做解释,有兴趣的可以参考文末的参考文献条目13。
3.1 相关定义 为了更好的把谱聚类问题转换为图论问题,定义如下概念(有些概念之前已定义,权当回顾下):
- 无向图
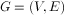 ,顶点集V表示各个样本,带权的边表示各个样本之间的相似度 ,顶点集V表示各个样本,带权的边表示各个样本之间的相似度 - 与某结点邻接的所有边的权值和定义为该顶点的度d,多个d 形成一个度矩阵
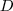 (对角阵) (对角阵)
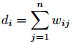
- 邻接矩阵
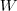 ,A子图与B子图之间所有边的权值之和定义如下: ,A子图与B子图之间所有边的权值之和定义如下:
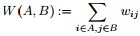
其中,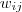 定义为节点 定义为节点 到节点 到节点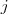 的权值,如果两个节点不是相连的,权值为零。 的权值,如果两个节点不是相连的,权值为零。
- 相似度矩阵的定义。相似度矩阵由权值矩阵得到,实践中一般用高斯核函数(也称径向基函数核)计算相似度,距离越大,代表其相似度越小。
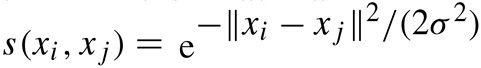
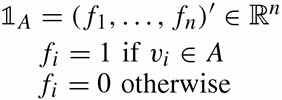
3.2 目标函数 因此,如何切割图则成为问题的关键。换言之,如何切割才能得到最优的结果呢?
举个例子,如果用一张图片中的所有像素来组成一个图 ,并把(比如,颜色和位置上)相似的节点连接起来,边上的权值表示相似程度,现在要把图片分割为几个区域(或若干个组),要求是分割所得的 Cut 值最小,相当于那些被切断的边的权值之和最小,而权重比较大的边没有被切断。因为只有这样,才能让比较相似的点被保留在了同一个子图中,而彼此之间联系不大的点则被分割了开来。
设 为图的几个子集(它们没有交集) ,为了让分割的Cut 值最小,谱聚类便是要最小化下述目标函数: 为图的几个子集(它们没有交集) ,为了让分割的Cut 值最小,谱聚类便是要最小化下述目标函数:
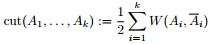
其中k表示分成k个组,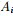 表示第i个组,[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/_]ZH3G$7MQZ]B[]C2[66%602B.tmp[/img] 表示第i个组,[img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/_]ZH3G$7MQZ]B[]C2[66%602B.tmp[/img]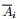 表示 表示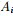 的补集, 的补集,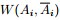 表示第 表示第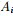 组与第 组与第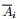 组之间的所有边的权重之和(换言之,如果要分成K个组,那么其代价就是进行分割时去掉的边的权值的总和)。 组之间的所有边的权重之和(换言之,如果要分成K个组,那么其代价就是进行分割时去掉的边的权值的总和)。 为了让被切断边的权值之和最小,便是要让上述目标函数最小化。但很多时候,最小化cut 通常会导致不好的分割。以分成2类为例,这个式子通常会将图分成了一个点和其余的n-1个点。如下图所示,很明显,最小化的smallest cut不是最好的cut,反而把{A、B、C、H}分为一边,{D、E、F、G}分为一边很可能就是最好的cut:
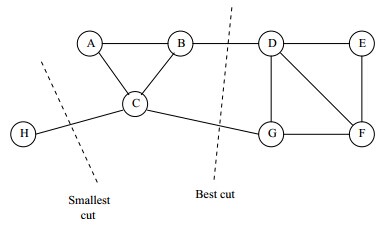
为了让每个类都有合理的大小,目标函数尽量让A1,A2...Ak 足够大。改进后的目标函数为:
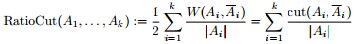
其中|A|表示A组中包含的顶点数目。 或:
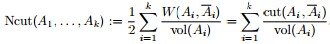
其中,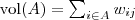 。 。 3.3 最小化RatioCut 与最小化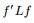 等价 等价 下面,咱们来重点研究下RatioCut 函数。 目标函数: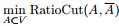
定义向量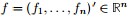 ,且: ,且:
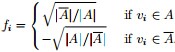
根据之前得到的拉普拉斯矩阵矩阵的性质,已知
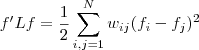
现在把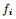 的定义式代入上式,我们将得到一个非常有趣的结论!推导过程如下: 的定义式代入上式,我们将得到一个非常有趣的结论!推导过程如下:
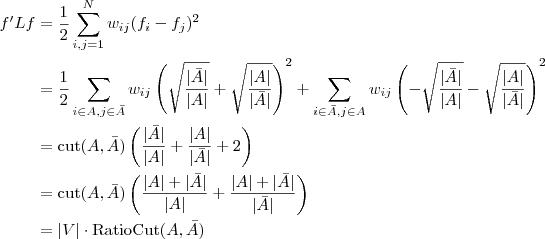
是的,我们竟然从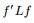 推出了RatioCut,换句话说,拉普拉斯矩阵L 和我们要优化的目标函数RatioCut 有着密切的联系。更进一步说,因为 推出了RatioCut,换句话说,拉普拉斯矩阵L 和我们要优化的目标函数RatioCut 有着密切的联系。更进一步说,因为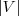 是一个常量,所以最小化RatioCut,等价于最小化 是一个常量,所以最小化RatioCut,等价于最小化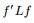 。 。 同时,因单位向量 的各个元素全为1,所以直接展开可得到约束条件: 的各个元素全为1,所以直接展开可得到约束条件: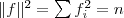 且 且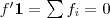 ,具体推导过程如下: ,具体推导过程如下:
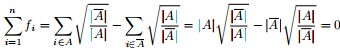
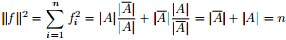
最终我们新的目标函数可以由之前的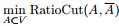 ,写成: ,写成:
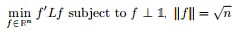
其中,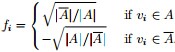 ,且因 ,且因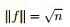 ,所以有:f'f = n(注:f是列向量的前提下,f'f是一个值,实数值,ff'是一个N*N的矩阵)。 ,所以有:f'f = n(注:f是列向量的前提下,f'f是一个值,实数值,ff'是一个N*N的矩阵)。 继续推导前,再次提醒特征向量和特征值的定义:
- 若数字
 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/B)4BU]3RZT8USPGGC%60@KS33.tmp[/img]和非零向量 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/B)4BU]3RZT8USPGGC%60@KS33.tmp[/img]和非零向量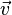 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/H%606(4A[)N52%J_%7D%7B@N]KP$N.tmp[/img]满足file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/EZ(LQ27(70ISGRB%7BBRRYPIR.tmp [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/H%606(4A[)N52%J_%7D%7B@N]KP$N.tmp[/img]满足file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/EZ(LQ27(70ISGRB%7BBRRYPIR.tmp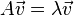 ,则 ,则 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/JQ2GJ%HE9X@FAX)_V_L9_8L.tmp为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/HY3TPN8WYCL8%7D(8M8(G4_H9.tmp file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/JQ2GJ%HE9X@FAX)_V_L9_8L.tmp为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/HY3TPN8WYCL8%7D(8M8(G4_H9.tmp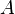 的一个特征向量, 的一个特征向量,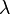 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7$VO8M%7BQ89GTP@@QHLIX9DN.tmp是其对应的特征值。 file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/7$VO8M%7BQ89GTP@@QHLIX9DN.tmp是其对应的特征值。
假定 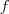 = =  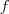 ,此刻, ,此刻, 是特征值, 是特征值,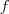 是 是 的特征向量。两边同时左乘 的特征向量。两边同时左乘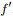 ,得到 ,得到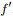  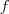 = =  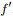 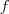 ,而f'f=n,其中n为图中顶点的数量之和,因此 ,而f'f=n,其中n为图中顶点的数量之和,因此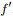  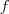 = =  n,因n是个定值,所以要最小化 n,因n是个定值,所以要最小化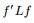 ,相当于就是要最小化 ,相当于就是要最小化 。因此,接下来,我们只要找到 。因此,接下来,我们只要找到 的最小特征值 的最小特征值 及其对应的特征向量即可。 及其对应的特征向量即可。 但到了这关键的最后一步,咱们却遇到了一个比较棘手的问题,即由之前得到的拉普拉斯矩阵的性质“ 最小的特征值为零,并且对应的特征向量正好为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/]88~FLV~U6@4_Z4]5QJF]BL.tmp 最小的特征值为零,并且对应的特征向量正好为file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/]88~FLV~U6@4_Z4]5QJF]BL.tmp ”可知:其不满足 ”可知:其不满足 的条件,因此,怎么办呢?根据论文“A Tutorial on Spectral Clustering”中所说的Rayleigh-Ritz 理论,我们可以取第2小的特征值,以及对应的特征向量 的条件,因此,怎么办呢?根据论文“A Tutorial on Spectral Clustering”中所说的Rayleigh-Ritz 理论,我们可以取第2小的特征值,以及对应的特征向量 。 。 更进一步,由于实际中,特征向量 里的元素是连续的任意实数,所以可以根据 里的元素是连续的任意实数,所以可以根据 是大于0,还是小于0对应到离散情况下的 是大于0,还是小于0对应到离散情况下的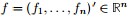 ,决定 ,决定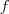 是取 是取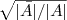 ,还是取 ,还是取 。而如果能求取 。而如果能求取 的前K个特征向量,进行K-means聚类,得到K个簇,便从二聚类扩展到了K 聚类的问题。 的前K个特征向量,进行K-means聚类,得到K个簇,便从二聚类扩展到了K 聚类的问题。
而所要求的这前K个特征向量就是拉普拉斯矩阵的特征向量(计算拉普拉斯矩阵的特征值,特征值按照从小到大顺序排序,特征值对应的特征向量也按照特征值递增的顺序排列,取前K个特征向量,便是我们所要求的前K个特征向量)!
所以,问题就转换成了:求拉普拉斯矩阵的前K个特征值,再对前K个特征值对应的特征向量进行 K-means 聚类。而两类的问题也很容易推广到 k 类的问题,即求特征值并取前 K 个最小的,将对应的特征向量排列起来,再进行 K-means聚类。两类分类和多类分类的问题,如出一辙。
就这样,因为离散求解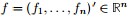 很困难,但RatioCut 巧妙地把一个NP难度的问题转换成拉普拉斯矩阵特征值(向量)的问题,将离散的聚类问题松弛为连续的特征向量,最小的系列特征向量对应着图最优的系列划分方法。剩下的仅是将松弛化的问题再离散化,即将特征向量再划分开,便可以得到相应的类别。不能不说妙哉! 很困难,但RatioCut 巧妙地把一个NP难度的问题转换成拉普拉斯矩阵特征值(向量)的问题,将离散的聚类问题松弛为连续的特征向量,最小的系列特征向量对应着图最优的系列划分方法。剩下的仅是将松弛化的问题再离散化,即将特征向量再划分开,便可以得到相应的类别。不能不说妙哉! 3.4 谱聚类算法过程 综上可得谱聚类的算法过程如下:
- 根据数据构造一个Graph,Graph的每一个节点对应一个数据点,将各个点连接起来(随后将那些已经被连接起来但并不怎么相似的点,通过cut/RatioCut/NCut 的方式剪开),并且边的权重用于表示数据之间的相似度。把这个Graph用邻接矩阵的形式表示出来,记为 [img]file:///C:/Users/zhoulei/AppData/Local/Temp/TempPic/VR%7DJL07I%60IL66AN%7BGMSB%7D[M.tmp[/img]
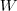 。 。 - 把
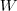 的每一列元素加起来得到 的每一列元素加起来得到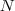 个数,把它们放在对角线上(其他地方都是零),组成一个 个数,把它们放在对角线上(其他地方都是零),组成一个 的对角矩阵,记为度矩阵 的对角矩阵,记为度矩阵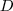 ,并把 ,并把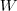 - - 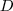 的结果记为拉普拉斯矩阵 的结果记为拉普拉斯矩阵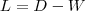 。 。 - 求出
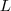 的前 的前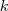 个特征值(前 个特征值(前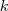 个指按照特征值的大小从小到大排序得到) 个指按照特征值的大小从小到大排序得到)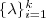 ,以及对应的特征向量 ,以及对应的特征向量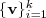 。 。 - 把这
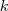 个特征(列)向量排列在一起组成一个 个特征(列)向量排列在一起组成一个 的矩阵,将其中每一行看作 的矩阵,将其中每一行看作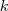 维空间中的一个向量,并使用 K-means 算法进行聚类。聚类的结果中每一行所属的类别就是原来 Graph 中的节点亦即最初的 维空间中的一个向量,并使用 K-means 算法进行聚类。聚类的结果中每一行所属的类别就是原来 Graph 中的节点亦即最初的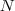 个数据点分别所属的类别。 个数据点分别所属的类别。
或许你已经看出来,谱聚类的基本思想便是利用样本数据之间的相似矩阵(拉普拉斯矩阵)进行特征分解( 通过Laplacian Eigenmap 的降维方式降维),然后将得到的特征向量进行 K-means聚类。 此外,谱聚类和传统的聚类方法(例如 K-means)相比,谱聚类只需要数据之间的相似度矩阵就可以了,而不必像K-means那样要求数据必须是 N 维欧氏空间中的向量。 | 








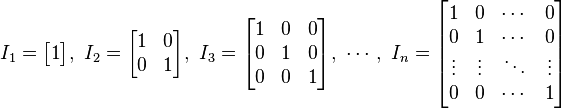
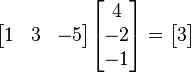




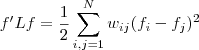
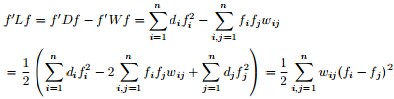
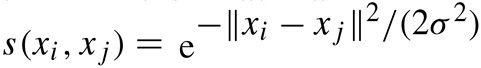
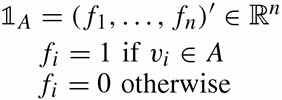

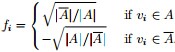
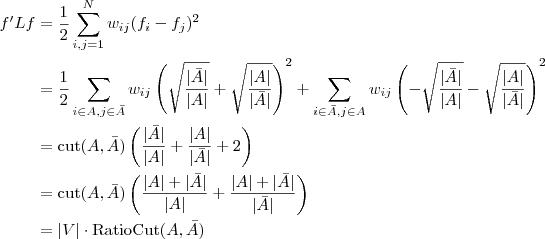
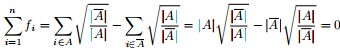














 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








