函数极限（三）

1.函数极限扩充后一共存在24种表达形式,可看成对变量x的6种情形与f(x)的4种情形的组合

2.保序性与夹逼性在极限是无穷大量情况下不生效,四则运算需要排除"待定型"

3.熟练掌握第一类和第二类重要极限

4.函数极限的柯西收敛原理有三种表达形式,利用数列柯西收敛原理与海涅定理证明

今天我们把函数极限的内容更新完毕。

传送门: 函数极限（一） 函数极限（二）

1

函数极限的扩充

我们从函数在一点的极限细分为左极限和右极限，一共三种极限。在此基础上，我们还能进一步扩充函数极限：

这样就6种情况。这些体现在极限分析表述哪里呢，我们再回顾一下函数极限定义：

红框就是对x的描述，以上的6种的表述变为：

剩下的是对极限的描述，有4种：

这样一共24种组合，可以把函数极限的定义扩充完毕。我们来几道例题看看：

• 例1

• 例2

对于函数极限的扩充，需要注意三点。第一就是关于函数性质，关于保序性和夹逼性，要排除无穷大量的情况，即保序性和夹逼性可以用在以下三种情形：

第二关于函数极限的四则运算需要排除“待定型”，即以下六种情况：

第三点就是关于海涅定理依然适用。比如对于x趋于正无穷大量时海涅定理表述如下：

2

第二类重要极限

• 例3

这里想表达的是，当x趋于无穷时，多项式只需要看最高次数项即可，极限由最高次数项决定。当x趋于0时，多项式的极限由最低次数项决定。

• 例4
  

函数极限开篇的时候，我们就介绍了第一类重要极限，除此之外，还有第二类重要极限.

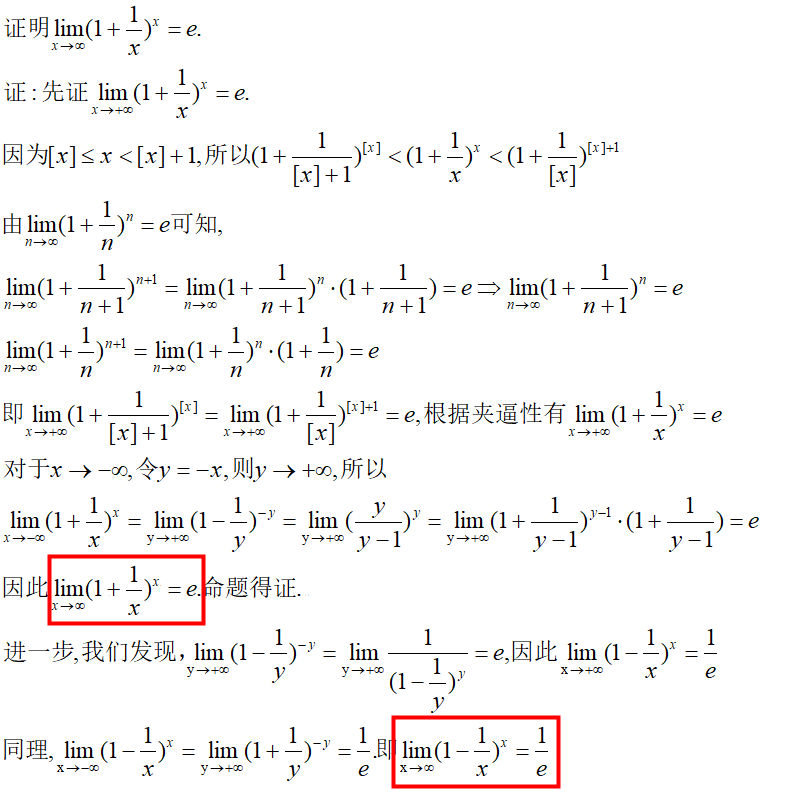
3

柯西收敛原理

表达数列收敛充分必要条件的是柯西收敛原理：

数列收敛的充分必要条件是该数列为基本数列

传送门：收敛准则（四）

在函数极限中，柯西收敛原理有三种形式：

我们证明第一种形式，其余类似。

证明充分性的时候，红色部分表明了f(xn)是基本数列，根据数列柯西收敛原理可以知道数列{f(xn)}收敛。然后黄色部分表达了归结原则的必要条件：对任意是无穷大量的数列都收敛。所以可得到函数极限收敛。

微积分的反常积分需要用到函数的柯西收敛原理，请必须深刻理解并掌握。