矩阵的掩码操作很简单。其思想是:根据掩码矩阵(也称作核)重新计算图像中每个像素的值。掩码矩阵中的值表示近邻像素值(包括该像素自身的值)对新像素值有多大影响。从数学观点看,我们用自己设置的权值,对像素邻域内的值做了个加权平均。
测试用例
思考一下图像对比度增强的问题。我们可以对图像的每个像素应用下面的公式:
![I(i,j) = 5*I(i,j) - [ I(i-1,j) + I(i+1,j) + I(i,j-1) + I(i,j+1)]\iff I(i,j)*M, \text{where }M = \bordermatrix{ _i\backslash ^j & -1 & 0 & +1 \cr -1 & 0 & -1 & 0 \cr 0 & -1 & 5 & -1 \cr +1 & 0 & -1 & 0 \cr }](https://i-blog.csdnimg.cn/blog_migrate/6392ed4cc96f2c8916a6086dc4789372.png)
上面那种表达法是公式的形式,而下面那种是以掩码矩阵表示的紧凑形式。使用掩码矩阵的时候,我们先把矩阵中心的元素(上面的例子中是(0,0)位置的元素,也就是5)对齐到要计算的目标像素上,再把邻域像素值和相应的矩阵元素值的乘积加起来。虽然这两种形式是完全等价的,但在大矩阵情况下,下面的形式看起来会清楚得多。
现在,我们来看看实现掩码操作的两种方法。一种方法是用基本的像素访问方法,另一种方法是用 filter2D 函数。
在对数字图像进行处理时,我们一般都会在空间域(spatial domain)或者频域(frequency domain)中进行。所谓“空间域”,实际上指的是图像本身,在空间域上的操作常常是改变像素点的值,也就是经过一个映射(我们所做的变换,如滤波等),将原来的f(x,y)变换为新的g(x,y)。而“频域”,它的数学基础是法国学者傅里叶提出的傅里叶级数和随后发展起来的傅里叶变换。在这其中起到重要作用的,就是电子计算机的不断完善和快速傅里叶变换(FFT)算法的提出。这些使得傅里叶变换成为了一中有力的分析和变换工具。就像一列波,我们在时间上观察,每个时刻的幅值是一个时间的函数。而当我们变换角度,从频率域上去看,又会发现它是一系列正弦波的叠加,而这些正弦波的频率都会是某个基波频率的整数倍。可谓“横看成岭侧成峰”!
在空间域的操作主要可以分为两类:第一类是所谓的“图像强度变换”(Intensity Transform),另一类是所谓的“空间域图像滤波”(Spatial Filtering)。这两者的区别主要是处理方法的不同。前者对单个像素点进行操作,例如通过阈值函数实现图形的二值化,实现灰度平均等。而后者建立在邻域(neighborhood)的概念上,讲究的是利用一个矩阵核(Kernel)对一个小区域进行操作。今天这篇文章主要介绍的是后者,以及如何用OpenCV中的函数去实现。
我们先来看下面的这个公式,以及它的矩阵表示形式:
这个公式到它的矩阵表示形式的转换相信并不复杂,稍有线性代数知识就可以看懂。而这种操作可以用来进行图像增强。那么我们如何来使用OpenCV中的函数进行操作呢?我们要用到filter2D这个函数。可以在帮助文档中查到,filter2D函数的功能是:Convolves an image with the kernel,即如何实现图像的卷积运算。其函数原型如下:
void filter2D(InputArray src, OutputArray dst, int ddepth, InputArray kernel, Point anchor=Point(-1,-1), double delta=0, int borderType=BORDER_DEFAULT ),可以用下面这个公式来说明:
让我们用代码来说明:








 本文介绍了OpenCV中掩码操作的概念及其在图像处理中的应用,特别是通过filter2D函数实现图像增强和平滑滤波。通过实例展示了如何使用掩码矩阵进行图像对比度增强,并与原始图像进行比较。此外,还探讨了空间域图像滤波的基本原理和矩阵表示,以及如何使用filter2D进行卷积运算。
本文介绍了OpenCV中掩码操作的概念及其在图像处理中的应用,特别是通过filter2D函数实现图像增强和平滑滤波。通过实例展示了如何使用掩码矩阵进行图像对比度增强,并与原始图像进行比较。此外,还探讨了空间域图像滤波的基本原理和矩阵表示,以及如何使用filter2D进行卷积运算。
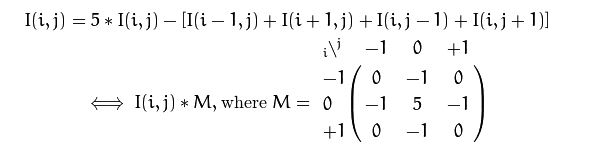
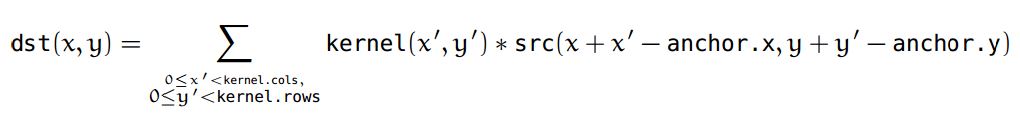
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 359
359

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








