1、Identifying influential nodes based on the disassortativity and community structure of complex network (基于复杂网络的异质性和社区结构识别关键节点 )
全文总结:本文重点关注基于网络的非同配性和社区结构来识别有影响力的节点。作者提出了节点非同配性的概念,它衡量节点度和其邻居节点度之间的不一致性。他们提出了一种称为节点非同配性(DoN)的度量来量化这一特性。论文还分析了节点非同配性、社区结构和节点影响力之间的关系。作者随后引入了一种称为mDC的影响力度量,它结合了非同配性和社区结构的信息,以更好地识别有影响力的节点。在合成和真实网络上的广泛实验表明,所提出的DoN和mDC方法优于现有的中心性度量,特别是在非同配网络和具有明显社区结构的网络中。论文还讨论了计算复杂性和对网络噪声和不准确性的稳定性的实际考虑。
- 文章研究背景和要解决的问题挑战
(1)复杂网络分析中,识别网络中有影响力的节点是一个重要的研究问题。传统的中心性度量方法往往忽略了网络社区结构对节点重要性的影响。
(2)节点的非同配性(disassortativity)和社区结构是影响节点重要性的两个关键因素。非同配性反映了网络中不同度数节点之间的连接关系,而社区结构则反映了网络中的模块化特征。
(3)如何结合节点非同配性和社区结构信息,提出更有效的节点影响力度量方法,是本文要解决的主要问题。
(4)在实际应用中,算法的计算复杂度和对网络噪声的稳定性也是需要考虑的重要挑战。动态网络拓扑变化和网络数据噪声会影响算法识别关键节点的性能。
传统中心度指标往往无法准确地识别出在网络中具有重要影响的关键节点,因为它们只考虑了局部信息。而DoN和mDC则能够更好地捕捉到节点之间复杂的异质性和社区结构,从而提高了在真实网络应用中的准确性。同时,这些指标也适用于大规模网络,具有较高的计算效率。
- 具体实现
该论文提出了两种新的网络中心度指标:Disassortativity of the Node(DoN)和Influential Metric of Nodes based on Disassortativity and Community Structure(mDC)。这些指标旨在更好地识别网络中的关键节点,并考虑了节点之间的异质性和社区结构的影响。
相比于传统的基于局部信息的度数中心度指标,如度数、介数中心度等,DoN和mDC考虑了更广泛的全局信息,包括节点的邻居及其邻接关系的类型。此外,它们还考虑了社区结构的影响,这对于许多现实世界的应用非常重要。
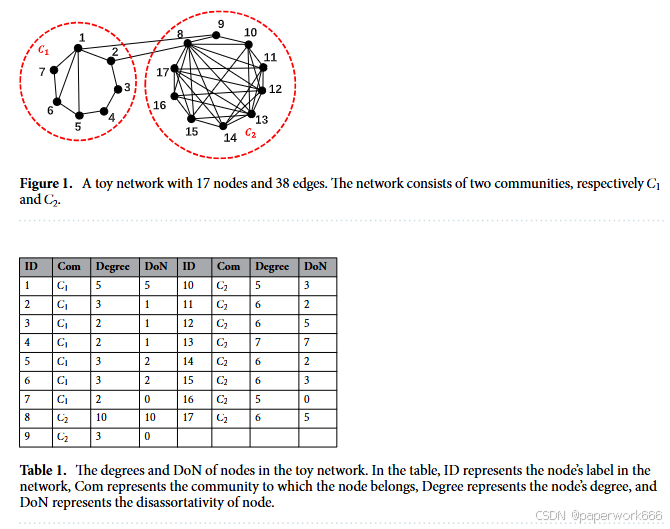
本文提出了一种基于节点非同配性和社区结构的新型节点影响力度量方法 mDC(Influential Metric of Node based on Disassortativity and Community structure)。其主要包括以下步骤:
-
定义节点非同配性(Disassortativity of Node, DoN)的概念和度量方法。DoN反映了节点与其邻居节点度数的差异程度,公式如下:
其中 d i d_i di 表示节点 i i i 的度数, N i N_i Ni 表示节点 i i i 的邻居节点集合, V_C_i 表示节点 i i i 所属的社区, d i n i d_{in_i} dini 表示与节点 i i i 同社区的邻居节点数, d o u t i d_{out_i} douti 表示与节点 i i i 不同社区的邻居节点数。 -
提出基于节点非同配性和社区结构的节点影响力度量方法 mDC。mDC 通过加权结合节点非同配性和社区边界受欢迎度来评估节点的影响力,公式如下:
其中 α i \alpha_i αi 表示节点 i i i 所属社区的社区系数,反映了该社区与其他社区的联系程度。 f c ( i ) f_c(i) fc(i) 表示节点 i i i 的社区边界受欢迎度。 -
提出了 mDC 算法的具体实现步骤,包括社区检测、社区系数计算、DoN 和 f c ( i ) f_c(i) fc(i) 的计算以及最终的 mDC 值计算。
总之,本文提出的 mDC 方法通过结合节点非同配性和社区结构信息,能够更准确地识别网络中的关键节点,为复杂网络分析提供了新的工具。
- 实验设计
本文主要介绍了针对复杂网络中识别重要节点的评价指标和算法,并通过一系列实验验证了这些方法的有效性。具体来说,文章首先分析了中心度指标(如度、介数、紧密度等)在不同网络结构下的表现,并提出了基于节点之间联系的度异质性指标来更准确地评估节点的重要性。接着,文章提出了一种新的影响力计算方法——mDC,该方法综合考虑了节点的度异质性和社区边界结构对信息传播的影响。最后,通过对合成网络和真实网络的数据分析,作者比较了不同的影响力计算方法的效果,并得出了mDC在识别重要节点方面具有较好性能的结论。
具体的实验包括以下几个部分:
对比中心度指标的表现:作者使用了多个中心度指标(如度、介数、紧密度等)来评估节点的重要性,并在不同网络结构下进行了测试。结果显示,在高度聚集的网络中,度中心度的表现最好,而在高度分散的网络中,介数中心度则更加有效。
分析度异质性指标的作用:作者提出了一种新的度异质性指标——DoN,用于衡量节点与其他节点之间的连接强度差异。实验结果表明,DoN可以更好地反映节点的重要程度,尤其是在高度聚集的网络中。
比较影响力计算方法的效果:作者将mDC与多个现有的影响力计算方法进行了比较,包括社区中心性、介数中心性、紧密度中心性等。实验结果表明,mDC在识别重要节点方面的效果优于其他方法。
总的来说,本文提出的度异质性指标和影响力计算方法为复杂网络中的节点识别提供了新的思路和工具,同时也为相关领域的研究提供了一些参考。


- 总结
值得精读
该研究提出了一种新的节点影响力度量指标mDC,能够有效地识别网络中的社区边界节点和核心节点。
研究使用了真实的博客网络数据,并通过实验验证了mDC在不同类型的网络中具有更好的性能表现。
研究还提出了一种基于步函数的度异质性度量指标DoN,可以用于评估节点之间的连接关系。
研究结果表明,在非异质性网络中,DoN和mDC能够有效识别出现有状态中心性指标无法识别的新重要节点。
研究提出了将局部信息与全局信息相结合的方法来评估节点的重要性。
研究引入了社区结构的概念,并将其与度异质性结合,提出了新的节点影响力度量指标mDC。
研究使用了步函数来计算度异质性,这种方法比传统的基于邻居节点度数的方法更加简单且易于实现。
- 局限性
将考虑非重叠社区划分,进一步探讨如何在重叠社区结构中有效识别关键节点。
将扩展DoN和mDC算法到网络的超球面表示中。
将探索如何利用动态网络信息来确定当前时刻网络的关键节点,以减少算法的时间复杂度和重复计算。
2、DomiRank Centrality reveals structural fragility of complex networks via node dominance (DomiRank 中心性揭示了复杂网络的结构脆弱性)
全文总结:本文介绍了一种新的中心性度量指标DomiRank,它可以量化节点在其各自邻域中的主导地位。DomiRank通过可调参数σ整合了局部和全局拓扑信息。作者表明,DomiRank在生成有针对性的攻击方面系统性地优于其他中心性指标,这些攻击能有效损害网络结构并破坏功能,适用于合成网络和现实世界网络。基于DomiRank的攻击还会造成更持久的损害,阻碍网络的反弹能力并损害系统的抗压性。作者提供了一个解析公式和一个高效的可并行算法来计算DomiRank,使其适用于大规模稀疏网络。
- 文章研究背景和要解决的问题挑战
(1). 复杂系统由许多相互作用的组件组成,其动态行为和出现的特性是系统属性。但并非所有系统组成部分在结构和动力学中都同等重要,有些元素可能对确保复杂系统结构或功能完整性至关重要。
(2). 准确高效地识别复杂系统的关键元素对于多种应用至关重要,如提供最合适的网络搜索结果、制定疾病传播缓解方案,以及确保交通网络和关键基础设施的完整性和功能。
(3). 网络理论通过将复杂系统抽象为节点(系统组成部分)和链接(相互作用)的集合,提供了一个评估节点相对重要性的通用框架,产生了不同的节点中心性定义。
(4). 中心性指标在设计提高网络鲁棒性和弹性的缓解策略中起着关键作用,这对于维持我们日常生活所依赖的互联基础设施至关重要。
- 具体实现
定义了一种新的中心性指标DomiRank,用于量化节点在其所在邻域的主导地位。
(1). DomiRank的定义如下:
d
Γ
(
t
)
d
t
=
α
A
(
θ
1
N
×
1
−
Γ
(
t
)
)
−
β
Γ
(
t
)
\frac{d\Gamma(t)}{dt} = \alpha A(\theta\mathbf{1}_{N\times 1} - \Gamma(t)) - \beta\Gamma(t)
dtdΓ(t)=αA(θ1N×1−Γ(t))−βΓ(t)
其中
Γ
(
t
)
\Gamma(t)
Γ(t)表示节点的DomiRank值,
A
A
A是网络的邻接矩阵,
α
\alpha
α和
β
\beta
β是控制竞争程度的参数,
θ
\theta
θ是主导阈值。
(2). 通过求解上述动态方程的稳态解,可以得到DomiRank的解析表达式:
Γ
=
θ
σ
(
σ
A
+
I
N
×
N
)
−
1
A
1
N
×
1
\Gamma = \theta\sigma(\sigma A + \mathbf{I}_{N\times N})^{-1}A\mathbf{1}_{N\times 1}
Γ=θσ(σA+IN×N)−1A1N×1
其中
σ
=
α
β
\sigma = \frac{\alpha}{\beta}
σ=βα。
(3). 为了提高计算效率,文章还提出了一种基于数值迭代的DomiRank计算方法:
Γ
(
t
+
d
t
)
=
Γ
(
t
)
+
(
σ
A
(
θ
1
N
×
1
−
Γ
(
t
)
)
−
Γ
(
t
)
)
d
t
\Gamma(t+dt) = \Gamma(t) + (\sigma A(\theta\mathbf{1}_{N\times 1} - \Gamma(t)) - \Gamma(t))dt
Γ(t+dt)=Γ(t)+(σA(θ1N×1−Γ(t))−Γ(t))dt
这种方法的计算复杂度为
O
(
m
+
N
)
\mathcal{O}(m+N)
O(m+N),其中
m
m
m是网络的边数,
N
N
N是节点数。
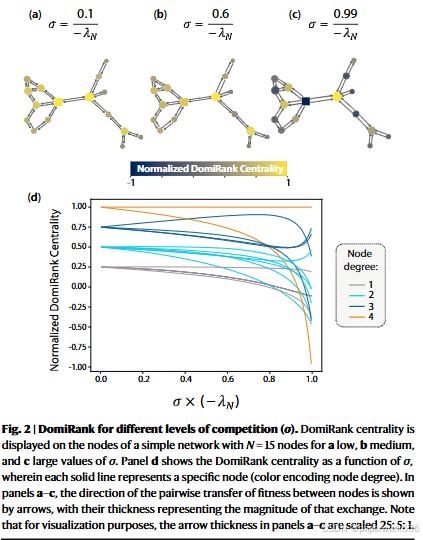
(4). 为了找到最优的竞争程度 σ ∗ \sigma^* σ∗,文章系统地探索了 σ \sigma σ的取值范围,并选择生成最有效攻击策略(即最小化网络最大连通分量的变化)的 σ ∗ \sigma^* σ∗作为最终结果。

- 实验设计
作者进行了以下对比实验:
DomiRank与其他中心性的比较:作者对三个不同拓扑结构的玩具网络(2D正则格子、Erdos-Renyi和Barabasi-Albert)进行了攻击测试,并发现DomiRank在这些网络中表现最好。作者还分析了其他九种中心性,包括Katz、PageRank等,发现它们的表现不如DomiRank。
DomiRank在不同网络拓扑结构中的应用:作者使用十个不同的网络拓扑结构(Watts-Strogatz、随机块模型、Erdos-Renyi、随机几何图、Barabasi-Albert等),并使用十个不同的攻击策略来测试DomiRank的性能。结果表明,在大多数情况下,DomiRank仍然是最有效的。
DomiRank在真实世界网络中的应用:作者对七个不同类型的真实世界网络(Ryanair连接、C-Elegans神经网络、美国西部电力网、高能物理arXiv引用网络、LiveJournal用户及其联系人、全美公路网络)进行了攻击测试,并发现DomiRank仍然表现出色。

- 总结
值得精读
该研究提出了一种新的中心度指标——Domirank,它能够根据网络拓扑结构的不同方面评估节点的重要性,并通过一个可调节参数来控制局部信息和全局信息之间的权衡。与PageRank相比,Domirank具有更低的计算成本和更快的收敛速度,并且可以并行化以提高效率。此外,该研究还探讨了Domirank在不同领域的应用前景,如垃圾邮件检测、疫苗接种策略和交通网络脆弱性评估等。
该研究提出了两种计算Domirank的方法:一种是解析法,另一种是数值法。其中,解析法需要求解稀疏矩阵的逆,对于大规模网络来说可能不可行;而数值法则可以通过递归方式实现,具有较低的计算成本。此外,该研究还引入了优化竞争水平的概念,即找到最小化最大连通组件面积的最优竞争水平,从而提高了攻击策略的有效性。
- 局限性
该研究为评估复杂系统中节点重要性的多样性提供了一个新思路,并为实际应用提供了可行性和实用性。未来的研究可以从以下几个方面展开:首先,可以进一步探索Domirank在不同领域中的应用,例如社交网络、生物网络等;其次,可以将Domirank与其他中心度指标进行比较,以验证其优越性;最后,可以考虑将Domirank应用于动态网络中,以更好地理解网络的演化规律。
3、A machine learning-based approach for vital node identification in complex networks(基于机器学习的复杂网络中关键节点识别方法)
全文总结:本文提出了一种基于机器学习的新颖方法来识别复杂网络中的关键节点。关键思想是在网络节点的一小部分(0.5%)上训练一个模型,使用捕捉节点连通性、度和核心性的特征。然后将训练好的模型用于预测网络中其余节点的重要性。该方法在与真实排名的相关性、适应动态参数变化的能力以及排名的唯一性方面优于现有最先进的方法。作者表明,使用RBF核的支持向量回归模型可以获得最佳结果。
- 文章研究背景和要解决的问题挑战
(1). 关键问题是如何识别复杂网络中最重要的节点(vital nodes)。这个问题在病毒营销、流行病分析等领域有重要应用 。
(2). 现有的方法主要基于数学表达式直接将节点的结构属性与其重要性联系起来。这些启发式方法在某些情况下表现良好,但适应性较弱,受限于特定设置和动力学 。
(3). 现有方法的主要缺点包括:
- 无法适应动力学参数的变化,无论采用SIR、SIS还是线性阈值模型,它们都会生成相同的重要性评分
- 计算过程复杂,难以总结概括
(4). 近期有少数基于机器学习的方法尝试解决这个问题,但存在以下问题:
- 需要大量(70%)的节点数据来训练模型,对于大型图计算代价高
- 使用自定义的节点重要性标签,可能引入偏差,无法准确反映节点重要性的顺序
现有方法存在适应性差、计算复杂度高、无法准确反映节点重要性排序等问题,这启发了本文提出一种新的基于机器学习的方法来解决这一挑战。
- 具体实现
本文提出的方法旨在解决这些问题,采用了一种基于机器学习的方法。与之前的工作不同,该方法不需要大量(70%)的节点数据来训练模型,也不使用自定义的节点重要性标签,从而避免了偏差的问题。
具体来说,该方法通过对节点的结构属性(如度、K-shell值、邻居信息等)进行建模,来近似预测节点的重要性。数学表达式如下:
M
C
D
E
(
u
)
=
α
K
S
(
u
)
+
β
∣
Γ
(
u
)
∣
+
γ
E
n
t
r
o
p
y
(
u
)
MCDE(u) = αKS(u) + β|Γ(u) | + γEntropy(u)
MCDE(u)=αKS(u)+β∣Γ(u)∣+γEntropy(u)
此外,该方法还采用了一种基于随机子图的方法来估计节点的实际影响力。作者理论上证明,只要采样足够多的随机子图,就可以以 1 − ε 1-ε 1−ε的精度近似得到节点的实际影响力。
与现有基于随机游走的方法不同,本文提出的方法不仅考虑了节点的结构属性,还能够适应不同的传播动力学模型,如SIR、SIS等。
本文提出了一种新颖的基于机器学习的方法来识别复杂网络中的关键节点,在计算复杂度、适应性和准确性等方面都有所改进。

本文提出的“EML”(Extended Machine Learning-based vital node identification)是一种基于机器学习的网络节点重要性识别算法。该算法主要分为三个步骤:特征工程、样本采集和模型训练。首先通过特征工程将每个节点表示为一个具有连通性、度数分布和核心度数的向量;然后通过采样获取有限数量的代表节点,并使用支持向量回归(SVR)等机器学习模型对其进行训练;最后根据训练好的模型计算出每个节点的EML分数,从而实现网络节点重要性的识别。
- 实验设计
本文主要介绍了在社交网络中识别关键节点的方法,并通过对比实验来验证不同方法的性能。具体来说,作者进行了以下四个对比实验:
排名与真实排名的相关性比较:作者使用了10个现有方法和提出的EML方法对8个网络数据集中的节点进行排名,并计算出每个方法的排名与真实排名之间的相关系数(即Kendall’s tau)。结果表明,EML方法在6个数据集中表现最好,在另外两个数据集中也取得了接近最优的表现。
影响概率对排名的影响比较:作者将EML方法应用于不同的影响概率下,观察其排名的变化情况。结果显示,当影响概率较小时,只有少数节点受到影响,导致模型学习到的信息较少,因此性能较差。而当影响概率较大时,模型的性能稳定性较好。
不同方法识别前k个关键节点的能力比较:作者使用Jaccard相似度作为评价指标,比较不同方法识别前k个关键节点的能力。结果显示,EML方法在这方面的表现优于其他方法。
不同方法的独特性排名能力比较:作者使用单调关系指标来衡量不同方法的独特性排名能力。结果显示,EML方法在这方面表现最佳,具有较高的独特性排名能力。
综上所述,EML方法在各项指标上的表现均优于其他方法,是一种有效的识别关键节点的方法。

- 总结
值得精读
论文提出了一种新颖的数据驱动机器学习方法来解决复杂网络中重要节点识别的问题。
该方法使用小部分节点的真实活力作为训练数据,并通过支持向量回归模型预测整个网络中每个节点的活力。
与现有的基于规则和启发式的方法相比,该方法在不同性能指标上表现更好,包括与真实排名的相关性、找到前k个最有影响力的节点的能力以及排名的独特性。
该方法具有通用性和数据驱动的设计,适用于各种类型的网络和动态情况。
论文还提出了一些改进方向,如使用更有效的模拟动态的方式获取真实活力数据、研究其他特征对排名的影响等。
该方法采用了数据驱动的机器学习方法,将网络结构和动力学信息结合起来,从而提高了识别重要节点的准确性。
该方法采用了代表性的采样策略,确保了训练集包含了不同结构和影响力属性的节点,同时限制了样本数量,使得即使对于大型网络也可以使用小型训练集。
该方法采用了支持向量回归模型,能够处理非线性关系,并且具有较高的准确性和稳定性。
- 局限性
可以进一步研究如何优化采样策略,以提高训练集的质量和代表性。
可以探索其他机器学习算法,如神经网络、决策树等,以寻找更好的模型。
可以研究如何将该方法扩展到更复杂的网络类型,如异质网络、时变网络等。
可以考虑将该方法应用于实际应用领域,如广告推荐、新闻传播等,以验证其实用性和效果。
4、Higher-order structure based node importance evaluation in directed networks(基于有向网络的高阶结构节点重要性评估 )
全文总结:本文提出了一个基于高阶结构特征,特别是前馈环路模式的评估有向网络中节点重要性的框架。传统的评估节点重要性的方法通常只考虑成对关系,忽略了更复杂的高阶相互作用的影响。通过结合前馈环路的结构特征,所提出的算法可以相比PageRank和特征向量中心性等经典方法提供更全面和准确的节点重要性评估。所提出方法的有效性通过在人工和实证引文网络数据上的实验得到验证,展示了改进的性能。此外,稳健性分析表明所提出的算法具有良好的稳定性。
- 文章研究背景和要解决的问题挑战
(1). 理解高阶结构在有向网络中的影响对于准确评估节点重要性至关重要。高阶结构可以提供比基本拓扑特征或一阶连接更深入的见解,揭示复杂的交互和关系。
(2). 现有的节点重要性评估方法通常只考虑成对关系,忽略了更复杂的高阶交互的影响。因此,需要开发一个综合框架,能够捕捉网络的全局和局部信息,反映高阶结构特征。
(3). 需要在人工网络和实际网络数据上验证所提出方法的实用性和有效性,并与经典方法进行比较。
- 具体实现
本文提出了一种基于高阶结构的节点重要性评估方法,适用于有向网络。该方法通过考虑节点之间的更复杂的关系来提高传统方法的准确性,并在实验中证明了其有效性。以下是本文提出的算法流程及关键公式:
1、构建高阶结构图:根据网络中的边权重构建出高阶结构图,其中每个节点表示一个节点对,边权表示两个节点对之间的关系强度。
2、 计算节点对的重要性得分:对于每个节点对,计算其重要性得分,即该节点对在网络传播过程中的影响力大小。本文提出了三种不同的计算方式:
(1)基于邻接矩阵的方式:利用邻接矩阵表示节点对之间的关系,通过计算节点对的度数来评估其重要性得分。
(2)基于转移概率矩阵的方式:将高阶结构图看作是一个随机游走模型,通过计算节点对的转移概率来评估其重要性得分。
(3)基于网络流的方式:将高阶结构图看作是一个最大流最小割问题,通过计算节点对的最大流量来评估其重要性得分。
其中,具体计算公式如下:
(1)基于邻接矩阵的方式:
s c o r e i j = ∑ k ∈ N ( i ) ∑ l ∈ N ( j ) w k l score_{ij} = \sum_{k \in N(i)} \sum_{l \in N(j)} w_{kl} scoreij=k∈N(i)∑l∈N(j)∑wkl
其中, N ( i ) N(i) N(i) 表示节点 i i i 的邻居集合, w k l w_{kl} wkl 表示节点对 ( k , l ) (k,l) (k,l) 之间的边权。
(2)基于转移概率矩阵的方式:
P i j = w i j ∑ k ∈ N ( i ) w i k P_{ij} = \frac{w_{ij}}{\sum_{k \in N(i)} w_{ik}} Pij=∑k∈N(i)wikwij
s c o r e i j = P i j × ∑ k ∈ N ( j ) P j k score_{ij} = P_{ij} \times \sum_{k \in N(j)} P_{jk} scoreij=Pij×k∈N(j)∑Pjk
其中, P i j P_{ij} Pij 表示从节点 i i i 到节点 j j j 的转移概率, ∑ k ∈ N ( j ) P j k \sum_{k \in N(j)} P_{jk} ∑k∈N(j)Pjk 表示从节点 j j j 出发能够到达的所有节点的转移概率之和。
(3)基于网络流的方式:
f l o w i j = m a x F l o w i j − m i n C u t i j flow_{ij} = maxFlow_{ij} - minCut_{ij} flowij=maxFlowij−minCutij
s c o r e i j = f l o w i j / m a x F l o w i j score_{ij} = flow_{ij} / maxFlow_{ij} scoreij=flowij/maxFlowij
其中, m a x F l o w i j maxFlow_{ij} maxFlowij 表示从节点 i i i 到节点 j j j 的最大流量, m i n C u t i j minCut_{ij} minCutij 表示从节点 i i i 到节点 j j j 的最小割容量。
3、计算节点的重要性得分:将所有节点对的重要性得分加权平均得到节点的重要性得分。

- 实验设计
本文主要介绍了对CDRank和CSRank算法的实验验证,包括人工网络数据和实证网络数据两部分。在人工网络数据中,作者构建了一个有向网络,并使用该网络进行了算法性能测试。在实证网络数据中,作者选择了美国物理学会期刊中的论文数据集,并使用该数据集对算法进行了评估。
在人工网络数据中,作者首先计算了节点的重要性评分与内在质量之间的相关系数rs,结果表明随着参数θ的增加,rs逐渐增大,且CSRank算法比CDRank算法表现更好。接着,作者选取了排名前5%的重要节点作为基准节点,并比较了不同算法下这些节点的平均排名。结果表明,当参数θ较小时,CDRank和CSRank算法相对于PageRank算法都有显著改善,而CSRank算法优于CDRank算法。此外,作者还分析了不同方法的top-L召回率Rc,并发现CDRank和CSRank算法相对于特征eigenvector centrality和PageRank算法,在所有检测长度L下都具有更高的召回率。
在实证网络数据中,作者使用了美国物理学会期刊中的论文数据集,并将其中的里程碑论文作为基准节点。结果显示,CDRank和CSRank算法相对于PageRank算法能够更好地识别出重要节点,尤其是当参数θ取值为0.2时,两种算法的平均排名均达到最小值。同时,CSRank算法的表现略好于CDRank算法。此外,作者还通过信息传播过程来验证算法的有效性,结果表明CDRank和CSRank算法在初始传播源的选择上更有效,可以更快地广泛传播信息。
最后,作者还对算法的鲁棒性进行了评估。他们模拟了一些恶意行为,如添加新的论文以增强已有论文的影响等,然后比较了不同算法在面对这些恶意行为时的稳定性。结果表明,基于节点度数的算法最容易受到恶意行为的影响,而CDRank和CSRank算法相对于PageRank算法更具鲁棒性,尤其是在参数θ较大时。
- 总结
值得精读
该研究提出了一种基于更高阶结构的有向网络中节点重要性的评估框架,能够更全面地反映网络中的复杂依赖关系,并且在实验中证明了其有效性。 具体来说,本文的优点包括:
- 考虑到了网络中的更高阶结构,提供了更准确的节点重要性评估;
- 基于PageRank算法,结合了有向环路的特征,构建了两种新的节点重要性评估算法;
- 在人工网络和科学引文网络上的实验证明了新算法的有效性和准确性;
- 比了不同算法的鲁棒性,表明新算法具有更强的鲁棒性。
方法创新点
- 本文的主要创新点在于将更高阶结构的信息引入到节点重要性评估中,通过构建基于PageRank算法的新算法来实现。具体来说,本文的方法创新点包括:
- 提出了基于有向环路的特征的节点重要性评估算法,能够更好地反映网络中的依赖关系;
- 将更高阶结构的信息与基本拓扑信息相结合,提高了节点重要性评估的准确性;
- 实验结果表明,新算法在评估节点重要性方面优于传统的PageRank算法和其他常见的评估方法。
- 局限性
本文提出的基于更高阶结构的有向网络中节点重要性的评估框架为未来的相关研究提供了一个很好的思路。未来的研究可以从以下几个方面展开:
- 进一步探究更高阶结构对节点重要性评估的影响,以及如何更好地利用这些信息;
- 研究其他类型的网络(如超图或简单复杂网络)中的节点重要性评估问题;
- 探索如何将机器学习等技术应用于节点重要性评估中,以提高评估的精度和效率。
5、Deep MinCut: Learning Node Embeddings by Detecting Communities(Deep MinCut:通过检测社区学习节点嵌入)
全文总结:本文提出了Deep MinCut (DMC),一种无监督的方法来学习图结构数据的节点嵌入。DMC根据节点所属的社区来得出节点表示,使得嵌入能够直接提供关于图结构的见解,而无需单独的聚类步骤。DMC通过最小化mincut损失来同时学习节点嵌入和社区,该损失捕获了社区之间连接的数量。作者证明了DMC学习到的社区是有意义的,并且节点嵌入在节点分类基准测试中优于传统的嵌入技术。
- 文章研究背景和要解决的问题挑战
(1). 研究背景:
- 图结构数据是复杂系统中实体关系的自然表示,如社交网络和信息网络。
- 为了在图上进行推断,需要学习节点嵌入,即将图的节点表示为向量形式,以捕捉节点之间的关系。
- 大多数实际图数据是无标签的,因此需要无监督的学习技术来学习节点嵌入。
(2). 要解决的问题挑战:
- 现有的无监督节点嵌入方法主要基于节点之间的相似性定义,如基于随机游走的共现概率。
- 作者认为节点嵌入不仅应该具有高质量的推断性能,还应该具有可解释性,能够直接反映图结构中的有趣模式,避免后续分析步骤的偏差。
- 因此,本文提出了一种无监督的节点嵌入学习方法Deep MinCut (DMC),能够同时学习节点嵌入和社区结构,从而使得节点嵌入具有可解释性。
- 具体实现
该论文提出了两种不同的方法来解决社区检测问题:基于谱分解的方法和基于神经网络的方法。
基于谱分解的方法首先将二进制矩阵P转换为实数矩阵H,并使用H的特征向量作为节点嵌入。然后通过最小化L H(L sym)来计算L P(A),其中L sym是归一化的拉普拉斯矩阵。这个过程可以通过求解H的特征值来实现。
基于神经网络的方法称为Deep MinCut,它使用一个编码器E θ来将每个节点映射到d维空间中。然后,通过对H中的元素进行采样,得到一个概率分布,并从中随机选择一个节点分配给社区。这个过程可以使用Gumbel-max技巧来实现,并且在训练过程中使用了直通Gumbel-softmax来提高收敛速度。
与传统的谱分解方法相比,Deep MinCut方法具有以下优点:
可以处理大型图形数据集。
能够学习节点嵌入并同时检测社区。
可以通过堆叠多个mincut损失函数来构建层次结构。
此外,该方法还提供了一种有效的批量训练方法,可以在GPU上高效地运行。

该论文的主要目标是解决社区检测问题,即在一个无向图中识别出一些子图,这些子图内的节点之间存在较强的联系,而与其他子图之间的联系较弱。社区检测在社交网络、生物信息学、推荐系统等领域都有广泛的应用。然而,由于图的规模和复杂性的增加,传统的谱分解方法变得难以扩展。因此,本文提出的Deep MinCut方法提供了一个更有效和可扩展的解决方案。
- 实验设计
本文主要介绍了作者在节点嵌入和社区检测方面的研究,并通过一系列实验来验证其方法的有效性。具体来说,作者进行了以下对比实验:
节点嵌入实验:该实验旨在比较DMC与传统节点嵌入方法的性能。作者使用了四个标准基准数据集(Cora、Citeseer、Pubmed和Wiki)来进行分类任务,并使用随机划分的方法来评估模型的泛化能力。结果表明,DMC在三个基准数据集上表现优于传统的社区检测和无监督学习方法,特别是在非标记的数据集上表现更好。
社区检测实验:该实验旨在比较DMC与其他解释性词嵌入方法的性能。作者使用Text8语料库构建了一个PPMI矩阵,并使用人类工人进行单词侵入测试来评估模型的可解释性。结果表明,DMC在精确度方面表现优于其他方法,并且能够生成具有意义的单词主题。
连接时间实验:该实验旨在分析训练时间和网络结构之间的关系。作者使用SBM生成了一些图形,并对不同的维度大小和连接概率进行了测试。结果表明,在适当的维度大小下,DMC的训练时间较短,并且能够更好地捕捉社区结构。
综上所述,本文的研究表明DMC是一种有效的节点嵌入和社区检测方法,能够在各种数据集上实现良好的性能,并且具有较高的可解释性和效率。


- 总结
值得精读
- 论文提出了一种新的无监督学习节点嵌入的方法,通过最小化min-cut损失函数来同时学习节点嵌入和社区结构。
- 研究者使用了Gumbel-Softmax技术,将节点嵌入与社区分配之间的关系建模为概率分布,并实现了连续可微分的过程,从而可以联合学习嵌入和社区。
- 论文在多个应用中展示了DMC的有效性,包括节点分类和社区检测等任务。
方法创新点
- 该研究提出了一个新的视角,即从社区的角度考虑节点相似性,而不是传统的基于随机游走或图摘要的方法。
- 通过最小化min-cut损失函数,可以更好地捕捉社区间的分离性和节点间的相似性,从而提高节点嵌入的质量和意义。
- 利用Gumbel-Softmax技术,可以实现连续可微分的过程,从而能够有效地学习节点嵌入和社区分配之间的关系。
- 局限性
- 可以进一步探索将min-cut损失应用于其他领域,如图像分割等,以扩展其应用范围。
- 由于min-cut损失假设存在图形结构,因此需要探索如何将其应用于没有明确图形结构的数据集上。
- 可以进一步探究如何利用min-cut损失学习更复杂的社区结构,例如层次化的社区结构。




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








