支持向量机(SVM)(三)

核函数

基于线性回归的知识我们可以把一个特征向量x映射到

$$\Phi(x)=\begin{bmatrix} x\\ x^2\\ x^3\\ \end{bmatrix}$$
为了代替SVM使用原来的输入属性 $x$,我们将要使用特征值$\phi(x)$，因此我们仅仅需要用 $\phi$代替原来算法中的 $x$。
由于算法有$<x,z>$的内积，意味着我们要用 <ϕ(x),ϕ(z)> <script type="math/tex" id="MathJax-Element-652"><\phi(x),\phi(z)></script>代替他。具体的，给定一个特征映射 $\phi$,我们可以定义对应的核函数为：
$K(x,z)=\phi(x)^T\phi(z)$
我们之前在算法中用到 <x,z> <script type="math/tex" id="MathJax-Element-655"> </script>的地方都将会用 $K(x,z)$代替。
现在，给定了 $\phi$之后，我们将会通过计算 $\phi(x)$和 $\phi(z)$的内积来计算 $K(x,z)$。当时通常计算 $K(x,z)$的代价可能会很大，甚至 $\phi$自己也会计算代价很大（可能是因为他是一个特别高的维数向量）。如何高效的计算 $K(x,z)$呢？我们可以在高维空间中给定 $\phi$,但是不需要显示的找到或表示出向量 $\phi(x)$
来看一个例子，假设 $x,z\in R^n$并且考虑 $K(x,z)=(x^Tz)^2 =\underset{i=1}{\overset{n}{\sum}}(x_i z_i)(\underset{i=1}{\overset{n}{\sum}}x_i z_i)$
$=\underset{i=1}{\overset{n}{\sum}}\underset{i=1}{\overset{n}{\sum}}x_ix_jz_iz_j$
$=\underset{i,j=1}{\overset{n}{\sum}}(x_ix_j)(z_iz_j)$
$=\phi(x)^T\phi(z)$
特征映射 $\phi$由下式给出(这里给定n=3)

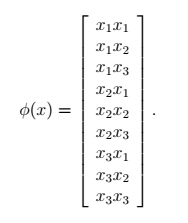
可以得到计算高纬度 $\phi(x)$需要 $O (n^2)$的时间复杂度，但 $K(x,z)$仅仅需要 $O(n)$的时间复杂度-与输入属性维数是线性关系。对于一个相似的核函数可以得到：

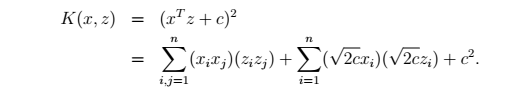
其对应的特征映射为(n=3)：

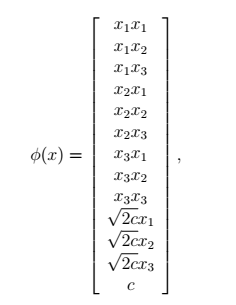
参数c控制着 $x_i$之间的相关权重。
更普遍的是，核函数 $K(x,z)=(x^Tz+c)^d$对应于特征映射到一个 $$\begin{pmatrix} n+d\\ d\\ \end{pmatrix}$$ 维的特征空间，然而尽管作用于 $O(n^d)$维的空间，但是计算 $K(x,z)$任然只需要 $O(n)$的复杂度，并且我们从不需要在高维的特征空间中显示的表示特征向量。
现在，让我们讨论一些不同的核函数。直观的，如果 $\phi(x)$和 $\phi(z)$离的很近，所以我们期望 $K(x,z)=\phi(x)^T\phi(z)$将会很大，相反的，如果 $\phi(x)$和 $\phi(z)$离的很远–也就是说相互之间几乎正交—那么 $K(x,z)=\phi(x)^T\phi(z)$可能会很小。因此，我们可以认为 $K(x,z)$是作为 $\phi(x)$和 $\phi(z)$或者 $x,z$相似度的测量。
有了这些直观感觉之后，假设你现在有一个学习问题，你提出了一些你认为可能合理测量 $x,z$之间相似度的核函数 $K(x,z)$。例如，你可能选择了：
$K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2})$
这是一个合理测量 $x,z$相似度的函数，并且当x,z接近是它等于1，远离时等于0。我们是否能使用这样的定义K作为 $SVM$的核函数呢？在这些特例中，回答是肯定的。（这个函数叫做 高斯核函数，并且对应于一个映射于无限维的特征映射 $\phi$。）但是给定一些函数K，我们怎么样判断它是否是一个有效的核函数；也就是说我们是否能找到一个特征向量 $\phi$使得 $K(x,z)=\phi(x)^T\phi(z)$对于所有的x,z都有效？
现在假设 $K$确实是一个对应于一些特征映射$\phi$有效的核函数。现在，考虑有限维m个点集 $\{x^{(1)},...,x^{(m)}\}$,乘方，得到一个m乘m维的矩阵K，定 $K_{(ij)}=K(x^{(i)},x^{(j)})$,这个矩阵叫做 核矩阵。既然我们已经重新定义了，我们使用 $K$既代表了核函数$K(x,z)$也代表了核矩阵 $K$,由于他们明显的相似关系。
现在如果$K$是一个有效的核函数，然后有 $K_{ij}=K(x^{(i)},x^{(j)})=\phi(x^{(i)})^T,\phi(x^{(j)})=\phi(x^{(j)})^T,\phi(x^{(i)})=K(x^{(j)},x^{(i)})=K_{ji}$，因此 $K$一定是一个对称矩阵。此外，让$\phi_k(x)$代表向量 $\phi$的第K个坐标，我们发现对于任意向量 $z$，我们有

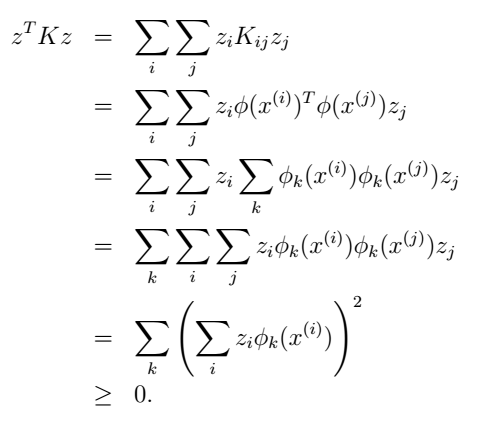
由于z是任意的，所以$K$是一个半正定矩阵。
因此，我们证明了如 $K$是一个有效的核函数(也就是说他对应于一些特征映射$\phi$),那么有对应的和矩阵 $K\in R^{m\times m}$是一个半正定矩阵。更平常的，这证明这不仅是必要，同时也是有效的条件对于K是个有效的核函数。

规则化和线性不可分情况

现在我们在SVM中用到的数据都假设他是线性可分的。当我通过$\phi$映射数据到高维特征空间时确实通常会增加我们数据的线性可分性，但是我们不能保证总会使这样。同时，我们不能保证我们找到的超平面就是我们想要的，他可能收到异常值的影响。例如，下面的左图显示这是一个最优化间隔分类器，但是当一个异常值加入后，它将会引起决定边界有一个显著的摆动，导致结果分类器有个更小的间隔。

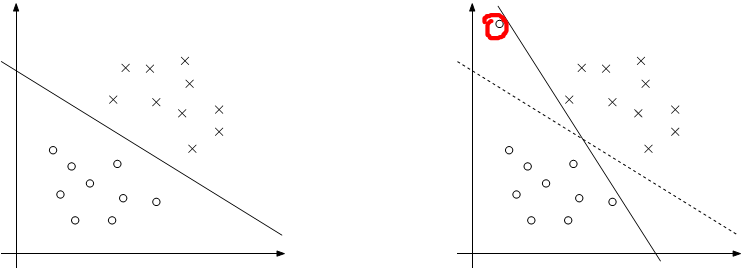
为了使这个算法对于非线性可分数据有效，并且对于异常值不敏感，我们重新定义我们的最优化方程为：

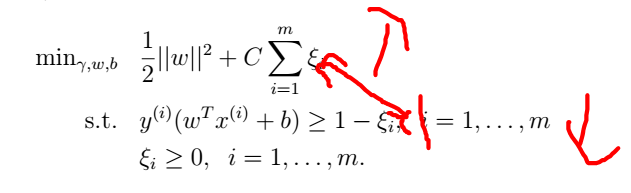
因此，现在允许样例函数间隔小于1，并且如果一个样例的函数间隔是$1-\xi$,我们可以通过**增加目标函数一个$C\xi_i$来补偿函数间隔。参数C用来控制使$||w||^2$变大（之前导致函数间隔变小）同时保证大部分样例函数间隔至少为1。
像之前那样我们可以定义拉格朗日方程为

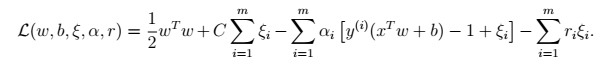
可以得到对偶问题为：

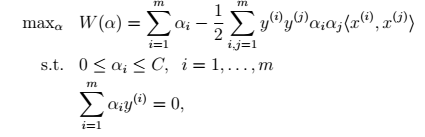
对于对偶问一唯一的改变是原来的约束条件$0\le\alpha_i$现在变成了$0\le\alpha_i\le C$。同时计算b的方式变了。
同时由于KKT对偶互补条件可以得到

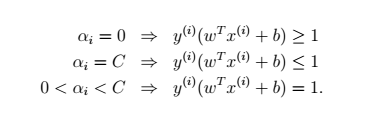
如何解对偶方程，将在接下来的文章中提到。