YaRN: Efficient Context Window Extension of Large Language Models翻译

摘要

旋转位置嵌入 (RoPE) 已被证明可以在基于 Transformer 的语言模型中有效地编码位置信息。然而，这些模型无法泛化到超过它们训练长度的序列。我们提出了 YaRN（另一种 RoPE 扩展方法），这是一种计算高效的方法，用于扩展此类模型的上下文窗口，与以前的方法相比，需要的token数少 10 倍，训练步骤少 2.5 倍。使用 YaRN，我们表明 LLaMA 模型可以有效地利用比原始预训练允许的更长的上下文长度，同时也超越了现有的上下文窗口扩展方面的最新技术。此外，我们还证明 YaRN 具有允许超越微调数据集的有限上下文进行外推的能力。我们在 https://github.com/jquesnelle/yarn 上发布了使用具有 64k 和 128k 上下文窗口的 YaRN 进行微调的 Llama 2 7B/13B checkpoint。

1.介绍

　　基于 Transformer 的大型语言模型 (LLM) 已表现出上下文学习 (ICL) 的强大能力，并且已成为许多自然语言处理 (NLP) 任务的几乎普遍的选择。Transformer 的自注意力机制使得训练高度并行化，允许以分布式方式处理长序列。LLM 训练的序列长度称为上下文窗口。
　　Transformer 的上下文窗口直接决定了可以提供样例的空间数量，从而限制了其 ICL 能力。然而，如果模型的上下文窗口有限，则为模型提供可执行 ICL 的鲁棒样例的空间就较小。此外，当模型的上下文窗口特别短时，其他任务（例如摘要）将受到严重阻碍。
　　根据语言本身的性质，token的位置对于有效建模至关重要，而自注意力由于其并行性，并不直接编码位置信息。在 Transformers 的架构中，通过引入了位置编码来解决这个问题。
　　最初的 Transformer 架构使用绝对正弦位置编码，后来改进为可学习的绝对位置编码。从那时起，相对位置编码方案进一步提高了 Transformer 的性能。目前，最流行的相对位置编码是 T5 相对偏差、RoPE、XPos 和 ALiBi。
　　位置编码的一个反复出现的限制是无法泛化到训练外看到的上下文窗口。虽然 ALiBi 等一些方法能够进行有限的泛化，但没有一种方法能够泛化到明显长于其预训练长度的序列。
　　已经做了一些工作来克服这种限制。[7]和同时[17]提出通过位置插值（PI）稍微修改RoPE并在少量数据上进行微调来扩展上下文长度。作为替代方案，我们在[4]的基础上提出了考虑了高频信息损失的“NTK-aware”插值。此后，我们提出了“NTK-aware”插值的两项改进，侧重点不同：

• 用于预训练模型的“动态 NTK”插值方法，无需微调。
• “NTK-by-part”插值方法在对少量较长上下文数据进行微调时表现最佳。

我们很高兴看到“NTK-aware”插值和“动态 NTK”插值已经出现在开源模型中，例如 Code Llama（使用“NTK-aware”插值）和 Qwen 7B（使用 “动态NTK”）。
　　在本文中，除了对“NTK-aware”、“动态 NTK”和“NTK-by-part”插值的先前工作进行完整说明之外，我们还提出了 YaRN（另一种 RoPE 扩展方法）， 一种有效扩展使用旋转位置嵌入 (RoPE) 训练的模型上下文窗口的方法，其中包括 LLaMA、GPT-NeoX 和 PaLM 系列模型。在对原始模型预训练数据的小于 ∼0.1% 大小的代表性样本进行微调后，YaRN 达到了最好的上下文窗口扩展。

2.Background and Related Work

2.1 Rotary Position Embeddings

我们工作的基础是[28]中介绍的旋转位置嵌入（RoPE）。给定一个输入token序列$w_1,w_2,\cdot \cdot \cdot ,w_L$，用${\text{x}}_1,\cdot \cdot \cdot ,{\text{x}}_L\in {\mathbb{R}}^{|D|}$表示它们的嵌入向量，其中$|D|$是隐藏状态的维度。按照[28]的表示法，注意力层首先将嵌入加上位置索引从而转换为query和key向量：
$${\text{q}}_m=f_q({\text{x}}_m,m)\in {\mathbb{R}}^{|L|},{\text{k}}_n=f_k({\text{x}}_n,n)\in {\mathbb{R}}^{|L|},\text{\hspace{1em}(1)}$$
其中$|L|$是每个头的隐藏维度。然后，注意力分数将被计算为：
$$softmax(\frac{{\text{q}}_m^T{\text{k}}_n}{\sqrt{|D|}}),$$
其中 ${\text{q}}_m,{\text{k}}_n$被视为列向量，我们只是计算分子中的欧几里得内积。在RoPE中，我们首先假设$|D|,|L|$是偶数，并将嵌入空间和隐藏状态识为复向量空间：
$${\mathbb{R}}^{|D|}\cong {\mathbb{C}}^{|D|/2},{\mathbb{R}}^{|L|}\cong {\mathbb{C}}^{|L|/2}$$
其中内积 ${\text{q}}^T\text{k}$ 成为了标准 Hermitian 内积 $Re({\text{q}}^{\ast }\text{k})$ 的实值部分。更具体地说，同构交替于实值部分和复数部分：
$$(({\text{x}}_m{)}_1,...,({\text{x}}_m{)}_d)\mapsto (({\text{x}}_m{)}_1+i({\text{x}}_m{)}_2,...,(({\text{x}}_m{)}_{|D|-1}+i({\text{x}}_m{)}_{|D|})),\text{\hspace{1em}(2)}$$
$$(({\text{q}}_m{)}_1,...,({\text{q}}_m{)}_l)\mapsto (({\text{q}}_m{)}_1+i({\text{q}}_m{)}_2,...,(({\text{q}}_m{)}_{|L|-1}+i({\text{q}}_m{)}_{|K|})).\text{\hspace{1em}(3)}$$
　　为了将嵌入${\text{x}}_m,{\text{x}}_n$ 转换为query向量和key向量，我们首先给出$\mathbb{R}-linear$操作：
$$W_q,W_k:{\mathbb{R}}^{|D|}\cong {\mathbb{C}}^{|D|/2}\to {\mathbb{R}}^{|L|}\cong {\mathbb{C}}^{|L|/2}.$$
　　在复数坐标中，函数$f_q,f_k$被表示为：
$$f_q({\text{x}}_m,m,{\theta }_d)=W_q{\text{x}}_m{e}^{im{\theta }_d},f_k({\text{x}}_n,n,{\theta }_d)=W_k{\text{x}}_n{e}^{in{\theta }_d},\text{\hspace{1em}(4)}$$
其中${\theta }_d=b^{-2d/|D|}$并且$b=10000$。这样做的要点是query向量和key向量之间的点积仅取决于相对距离$m-n$，如下所示：
$$⟨f_q(\text{x},m),f_k({\text{x}}_n,n){⟩}_{\mathbb{R}}\text{\hspace{1em}(5)}$$
$$=Re(⟨f_q(\text{x},m),f_k({\text{x}}_n,n){⟩}_{\mathbb{C}})\text{\hspace{1em}(6)}$$
$$=Re({\text{x}}_m^{\ast }{W}_q^{\ast }{W}_k{\text{x}}_n{e}^{i\theta (m-n)})\text{\hspace{1em}(7)}$$
$$=g({\text{x}}_m,{\text{x}}_n,m-n).\text{\hspace{1em}(8)}$$
在实数坐标中，RoPE能够被写为如下所示：

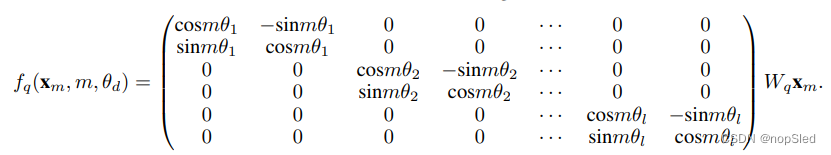
2.2 Positional Interpolation

由于语言模型通常是使用固定的上下文长度进行预训练的，因此很自然地会问如何通过对相对较少的数据进行微调来扩展上下文长度。对于使用 RoPE 作为位置嵌入的语言模型，[7] 和/u/kaiokendev [17] 同时提出了位置插值（PI）来将上下文长度扩展到超出预训练的限制。虽然PI在直接外推到大于预训练限制的序列$w1,\cdot \cdot \cdot \cdot ,w_L$时表现不佳，但他们发现，在少量微调的帮助下，在预训练限制内插值位置索引效果很好。具体来说，给定一个带有 RoPE 的预训练语言模型，他们通过以下方式修改 RoPE：
$$f_q^{\prime }({\text{x}}_m,m,{\theta }_d)=f_q({\text{x}}_m,\frac{m{L}^{\prime }}{L},{\theta }_d),f_k^{\prime }({\text{x}}_n,n,{\theta }_d)=f_k({\text{x}}_n,\frac{n{L}^{\prime }}{L},{\theta }_d)\text{\hspace{1em}(9)}$$
其中 $L\prime >L$ 是超出预训练限制的新上下文窗口。利用原始的预训练模型加上修改后的 RoPE 公式，他们在少了几个数量级的token（[7] 中为几十亿）上进一步微调语言模型，并成功实现了上下文窗口扩展。

2.3 Additional Notation

由于我们假设 RoPE 嵌入的插值在 (q,k) 和 (sin, cos) 域中都是对称的，因此我们将方程 9 重写并简化为以下一般形式：
$$f_{q,k}^{\prime }({\text{x}}_m,m,{\theta }_d)=f_{q,k}({\text{x}}_m,g(m),h({\theta }_d))\text{\hspace{1em}(10)}$$
其中对于PI，有
$$s=\frac{L^{\prime }}{L}\text{\hspace{1em}(11)}$$
$$g(m)=s\cdot m\text{\hspace{1em}(12)}$$
$$h({\theta }_d)={\theta }_d\text{\hspace{1em}(13)}$$
值 s 通常也称为上下文长度扩展的缩放因子。
　　在后续章节中，每当我们引入新的插值方法时，我们只需要指定函数$g(m)$和$h({\theta }_d)$。
　　此外，我们将 ${\lambda }_d$ 定义为在维度 $d$ 处 RoPE 嵌入的波长：
$${\lambda }_d=2\pi b^{\frac{2d}{|D|}}\text{\hspace{1em}(14)}$$
对于基数$b$、维度$d$ 和维度总数$|D|$。波长描述了在$d$维 RoPE 嵌入执行完整旋转 (2π) 所需的token长度。它在最低维度处最高，在最高维度处最低。
　　考虑到某些插值方法（例如位置插值）不关心维度的波长，我们将这些方法称为“盲”插值方法，而其他插值方法（例如 YaRN）则将其归类为“目标”插值方法。

2.4 Related work

ReRoPE 同样旨在扩展使用 RoPE 预训练的现有模型的上下文大小，并声称无需任何微调即可实现“无限”上下文长度。在 Llama 2 13B 模型上，随着上下文长度增加到 16k，损失单调递减支持了这一说法。它通过修改注意力机制来实现上下文扩展，因此并不是纯粹的嵌入插值方法。由于它目前与 Flash Attention 2 不兼容，并且在推理过程中需要两次注意力传递，因此我们不考虑将其进行比较。
　　与我们的工作同时，LM-Infinite 提出了与 YaRN 类似的想法，但侧重于非微调模型的“即时”长度泛化。由于它们还修改了模型的注意力机制，因此它不是嵌入插值方法，并且不能立即与 Flash Attention 2 兼容。

3.Methodology

尽管 PI 同等地拉伸所有 RoPE 维度，但我们发现 PI 描述的理论插值界限不足以预测 RoPE 和 LLM 内部嵌入之间的复杂动态。在下面的小节中，我们将分别描述我们识别和解决 PI 的主要问题，以便为读者提供我们协同使用的每种方法的背景、起源和理由，以最终获得完整的 YaRN 方法。

3.1 Loss of High Frequency information - “NTK-aware” Interpolation

如果我们仅从信息编码的角度来看待 RoPE，[30] 中表明，使用神经正切核（NTK）理论，如果输入维度较低且相应的嵌入缺乏高频组件，则深度神经网络将难以学习高频信息。在这里我们可以看到相似之处：token的位置信息是一维的，而 RoPE 将其扩展为 n 维复向量嵌入。
　　RoPE 在许多方面与傅里叶特征非常相似，因为可以将 RoPE 定义为傅里叶特征的特殊一维情况。不加区别地拉伸 RoPE 嵌入会导致丢失重要的高频细节，而网络需要这些高频细节来解析非常相似且非常接近的token（描述最小距离的旋转不需要太小，以使网络能够能够检测到）。
　　我们假设，在对 PI 中看到的较大上下文长度进行微调后，短上下文长度的困惑度略有增加可能与此问题有关。在理想情况下，对较大上下文长度的微调不会降低较小上下文长度的性能。
　　为了解决 RoPE 嵌入插值时丢失高频信息的问题，[4]中开发了“NTK-aware”插值。与将 RoPE 的每个维度均等地缩放 $s$ 倍不同，我们是通过减少高频缩放和增加低频缩放来将插值压力分散到多个维度。可以通过多种方式获得这种变换，但最简单的方法是对 $\theta$ 的值进行基础更改。
　　由于我们希望最低频率的缩放与线性位置缩放一样多，而最高频率保持恒定，因此我们需要找到一个新的基$b^{\prime }$，使得最后一个维度与具有缩放因子$s$的线性插值的波长相匹配。由于原始 RoPE 方法跳过奇数维度以便将$cos(\frac{2\pi x}{\lambda })$和$sin(\frac{2\pi x}{\lambda })$分量拼接到单个嵌入中，因此最后一个维度$d\in D$是$|D|-2$.
　　求解 $b\prime$ 得出：
$${b^{\prime }}^{\frac{|D|-2}{|D|}}=s\cdot b^{\frac{|D|-2}{|D|}}\text{\hspace{1em}(15)}$$
$$b^{\prime }=b\cdot s^{\frac{|D|}{|D|-2}}\text{\hspace{1em}(16)}$$
按照第 2.3 节的表示法，“NTK-aware”插值方案只是应用到基数变化公式，如下所示：
$$g(m)=m\text{\hspace{1em}(17)}$$
$$h(\theta )={b^{\prime }}^{-2d/|D|}\text{\hspace{1em}(18)}$$
　　在我们的测试中，与 PI 相比，该方法在扩展非微调模型的上下文大小方面表现得更好。然而，这种方法的一个主要缺点是，考虑到它不仅仅是一种插值方案，某些维度会稍微外推到“越界”值，因此使用“NTK -aware”插值进行微调会产生比PI差的结果。此外，由于“越界”值，理论缩放因子s不能准确地描述真实的上下文扩展比例。实际上，对于给定的上下文长度扩展，缩放值 s 必须设置为高于预期的比例。
　　在本文发布前不久，Code Llama 发布，它通过手动将基数 $b$ 设置为 1M 来使用“NTK-aware”缩放。

3.2 Loss of Relative Local Distances - “NTK-by-parts” Interpolation

RoPE 嵌入的一个有趣的观察是，给定上下文大小$L$，有一些维度$d$，其中波长比预训练期间看到的最大上下文长度，即$\lambda >L$，这表明某些维度的嵌入可能在旋转域中分布不均匀。
　　在 PI 和“NTK-aware”插值的情况下，我们同等对待所有 RoPE 隐藏维度（因为它们对网络具有相同的影响）。然而，我们通过实验发现网络对某些维度的处理方式与其他维度不同。如前所述，给定上下文长度$L$，某些维度的波长$\lambda$大于或等于$L$。假设当隐藏维度的波长大于或等于$L$时，所有位置对都编码了唯一的距离，我们假设绝对位置信息被保留，而当波长较短时，网络仅可获得相对位置信息。
　　当我们通过比例 $s$ 或使用基数变化 $b^{\prime }$ 拉伸所有 RoPE 维度时，所有token都会变得彼此更接近，因为以较小角度旋转的两个向量的点积更大。这种扩展严重削弱了LLM理解其内部嵌入之间的小型和局部关系的能力。我们假设这种压缩会导致模型对附近token的位置顺序感到困惑，从而损害模型的能力。
　　为了解决这个问题，考虑到我们在这里发现的观察结果，我们选择不插值更高的频率维度。尤其是：

• 如果波长 $\lambda$ 远小于上下文长度 $L$，我们不进行插值；
• 如果波长 $\lambda$ 等于或大于上下文长度 $L$，我们只想进行插值并避免任何外推（与之前的“NTK-aware”方法不同）；
• 位于两者间的维度，采用类似于“NTK-aware”的插值。

为了找到我们想要的维度$d$，给定特定上下文长度$L$下的完整旋转 $r$ 的数量，我们可以扩展方程14 如下：
$${\lambda }_d=2\pi b^{\frac{2d}{|D|}}\text{\hspace{1em}(19)}$$
$$r=\frac{L}{{\lambda }_d}\text{\hspace{1em}(20)}$$
求解$d$得出：
$$d=\frac{|D|}{2ln(b)}ln(\frac{L}{2\pi r})\text{\hspace{1em}(21)}$$
　　我们还提出，所有满足$r<\alpha$的维度$d$是我们通过缩放$s$线性插值的维度（与 PI 完全相同，避免任何外推），并且$r>\beta$根本不进行插值（总是外推）。定义斜坡函数 ${\gamma }_d$ 为：
$${\gamma }_d(r)=\{\begin{array}{ll}0,& ifr<\alpha \\ 1,& ifr>\beta \\ \frac{r-\alpha }{\beta -\alpha },& otherwise\end{array}\text{\hspace{1em}(22)}$$
　　借助斜坡函数，我们将新波长定义为：
$${\lambda }_d^{\prime }=(1-{\gamma }_d)s{\lambda }_d+{\gamma }_d{\lambda }_d.\text{\hspace{1em}(22)}$$
$\alpha$和$\beta$的值应根据具体情况进行调整。例如，我们通过实验发现，对于 Llama 系列模型，$\alpha$和$\beta$的最佳值为$\alpha =1$和$\beta =32$。
　　将 ${\lambda }_{d}d$ 转换为${\theta }_{d}d$后，该方法可以描述为：
$$g(m)=m\text{\hspace{1em}(24)}$$
$$h({\theta }_d)=(1-{\gamma }_d)\frac{{\theta }_d}{s}+{\gamma }_d{\theta }_d\text{\hspace{1em}(25)}$$
使用本节中描述的技术，生成的方法的变体以“NTK-by-parts”插值的名称发布。这种改进的方法比之前的 PI 和“NTK-aware” 插值方法表现得更好，无论是使用非微调模型还是微调模型。由于该方法避免了外推旋转域中分布不均匀的维度，因此它避免了以前方法中的所有微调问题。

3.3 Dynamic Scaling - “Dynamic NTK” Interpolation

当使用 RoPE 插值方法扩展上下文大小而不进行微调时，我们希望模型在较长的上下文大小下优雅地降级，而不是在尺度 $s$ 设置为更高的值时在整个上下文大小上进行完全降级。回想一下 2.3 节中的 PI 中的 $s=L\prime /L$，其中 $L$ 是经过训练的上下文长度，$L\prime$是新扩展的上下文长度。在“Dynamic NTK”方法中，我们动态计算尺度s如下：
$$s=\{\begin{array}{ll}\frac{L^{\prime }}{L},& if\frac{L^{\prime }}{L}>1\\ 1,& otherwise\end{array}\text{\hspace{1em}(26)}$$
　　当超过上下文大小时，在推理过程中动态更改缩放比例可以让所有模型优雅地降级，而不是在达到训练的上下文限制 $L$ 时立即中断。
　　将动态扩展与 kv 缓存结合使用时必须小心，因为在某些实现中，RoPE 嵌入会被缓存。正确的实现应该在应用 RoPE 之前缓存 $kv$ 嵌入，因为每个token的 RoPE 嵌入会随着$s$的变化而变化。

3.4 Increase in Average Minimum Cosine Similarity for Long Distances - YaRN

即使我们解决了 3.2 节中描述的局部距离问题，也必须在阈值 $\alpha$ 处插值更大的距离，以避免外推。直观上，这似乎不是问题，因为全局距离不需要高精度就能区分token位置（即网络只需要大致知道token是否位于序列的开头、中间或末尾） 。然而，我们发现，由于平均最小距离随着token数量的增加而变得更近，因此它使注意力 softmax 分布变得“尖峰”（即减少了注意力 softmax 的平均熵）。换句话说，随着长距离衰减的影响因插值而减弱，网络“更加关注”更多的令牌。这种分布的转变导致LLM的输出下降，这与之前的问题无关。
　　由于当我们将 RoPE 嵌入插入到更长的上下文大小时，注意力 Softmax 分布中的熵会减少，因此我们的目标是扭转熵的减少（即增加注意力logits的“温度”）。这可以通过在应用 softmax 之前将中间注意力矩阵乘以温度 $t>1$ 来完成，但由于 RoPE 嵌入被编码为旋转矩阵，我们可以简单地按常数因子 $\sqrt{t}$ 缩放 RoPE 嵌入的长度。“长度缩放”技巧使我们能够避免对注意力代码进行任何修改，这显着简化了与现有训练和推理管道的集成，并且时间复杂度为 O(1)。
　　由于我们的 RoPE 插值方案对 RoPE 维度的插值不均匀，因此很难计算相对于尺度 $s$ 所需的温度$t$的解析解。幸运的是，我们通过实验发现，通过最小化困惑度，所有 Llama 模型都遵循大致相同的拟合曲线：
$$\sqrt{t}\approx 0.1ln(s)+1$$
　　上述方程是通过在 LLaMA 7b、13b、33b 和 65b 模型上使用 3.2 中描述的插值方法，在不微调的情况对 $\sqrt{t}$ 进行拟合，使得困惑度相对于规模扩展因子$s$最低而得出的。我们还发现这个方程相当适用于 Llama 2 模型（7b、13b 和 70b），只有细微的差别。它表明熵增加的这种特性在不同的模型和训练数据中是常见的和可推广的。
　　最终的修改产生了我们最终的 YaRN 方法，其中 3.2 中描述的方法与 3.4 中描述的方法相结合，在训练和推理过程中使用。它在微调和非微调场景上都超越了之前的所有方法，并且完全不需要修改推理代码。只需要对最初生成 RoPE 嵌入的算法进行修改。YaRN 的简单性使其可以在所有推理和训练库中轻松实现，包括与 Flash Attention 2 的兼容性。

3.5 Extrapolation and Transfer Learning