【电路原理学习笔记】第3章：欧姆定律：3.1 电压、电流与电阻的关系

第3章：欧姆定律

3.1 电压、电流与电阻的关系

欧姆定律指出：电流与电压成正比，与电阻成反比。即$I=\frac{V}{R}$

3.1.1 电压与电流之间的线性关系

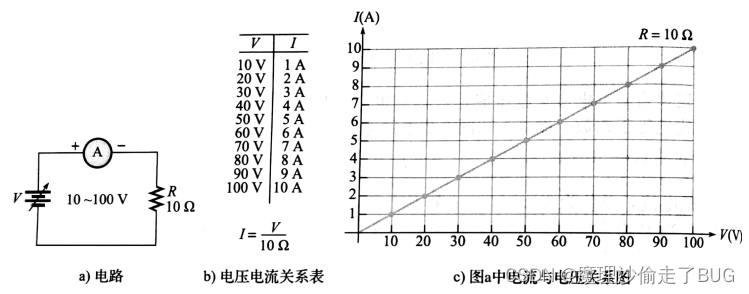
数学上，线性指的是变量之间的关系在图形上是一条直线。线性方程所对应的直线可以通过或不通过原点。当直线通过原点时，变量间成正比关系，方程的形式是$y=kx$ ，换到欧姆定律里面就是：电阻R是常数。

【例3-1】在图3-3所示电路中，请说明如果电压增加到当前值的3倍，则电流也变为当前值的3倍。

【解】根据欧姆定律，当前电流为$I=\frac{V}{R}=\frac{10\mathrm{V}}{4.7\mathrm{k\Omega }}=2.13\mathrm{mA}$
当电压增加到当前值的三倍时，有电流$I_1=\frac{V_1}{R}=\frac{30\mathrm{V}}{4.7\mathrm{k\Omega }}=6.38\mathrm{mA}$

【同步练习】如果图3-3中的电压变为4倍，那么电流会变为4倍吗？
【答】会

【例3-2】假设在一个工作电压为25V的电阻电路中测量电流，电流表读数为50mA，后来发现电流下降到40mA。假设电阻没有改变，可以断定电压已经改变。问新的电压是多少？
【解】根据欧姆定律，电阻是不变的，不需要根据电阻值来计算新电压，电流变化的百分比即为电压变化的百分比，所以新电压为$V_1=V\times \frac{I_1}{I}=V\times \frac{40\mathrm{mA}}{50\mathrm{mA}}=V\times 80\%=25\mathrm{V}\times 80\%=20\mathrm{V}$

3.1.2 电流与电阻的反比例关系

欧姆定律指出，电流与电阻成反比，即I=V/R。当电阻减小时，电流上升；当电阻增加时，电流下降。例如，如果电源电压保持恒定，电阻减半，电流加倍；电阻加倍，电流减半。
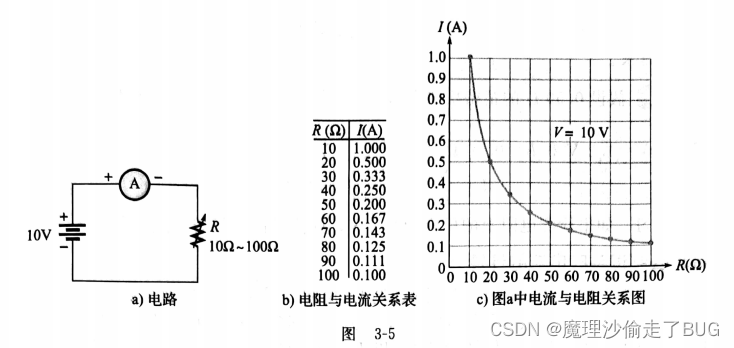
取一个恒定的电压值(例如10V),然后计算图3-5a中在10～1000范围内几个电压值下的电流。计算结果如图3-5b所示。I与R的关系如图3-5c所示。当两个变量成反比例时，这两个变量的乘积是常数，方程的形式是$xy=k$。

课后习题

（1）欧姆定律描述了3个电气量之间的关系，这些量是什么？
【答】电流、电压和电阻。

（2）写出计算电流的欧姆定律公式。
【答】$I=\frac{V}{R}$

（3）写出计算电压的欧姆定律公式。
【答】$V=IR$

（4）写出计算电阻的欧姆定律公式。
【答】$R=\frac{V}{I}$

（5）如果一个定值电阻上的电压增加了3倍，电流是增加还是减少，电流改变多少？
【答】在一个定值电阻上，电压增加3倍，电流也增加3倍。

（6）如果一个固定电阻上的电压减半，电流会改变多少？
【答】在一个定值电阻上，电压减半，电流也减半。

（7） 电阻上的电压固定，测得电流是1A。替换成2倍的电阻后，测量的电流是多少？
【答】电压固定时，电阻与电流成反比，电阻增加2倍，电流减为原来的$\frac{1}{2}$，即电流为0.5A。

（8）在某电路上，电压加倍，并且电阻减半，那么电流是增加还是减少，如果电流发生改变，那么怎么改变？
【答】根据欧姆定律