Stanford机器学习__Lecture notes CS229.Regularization and model selection（规则化和模型选择）

Stanford机器学习__Lecture notes CS229.Regularization and model selection（规则化和模型选择）

---

问题

模型选择问题：对于一个学习问题，我们实现并不会知道他的分布规律到底是什么，我们需要做出多种模型假设。比如要拟合一组样本点，可以使用线性回归$y=\theta^Tx$，也可以用多项式回归$y=\theta^Tx^{1→m}$。那么使用哪种模型好呢?（Bias-Variance Tradeoff（权衡偏差与方差））？

还有一类参数选择问题：如果我们想使用带权值的回归模型，那么怎么选择权重w公式里的参数$\tau$？

形式化定义：假设可选的模型集合是$M=(m_1,m_2...m_p)$

交叉验证（Cross validation）

这一部分其实我们在（Bias-Variance Tradeoff（权衡偏差与方差））中就有说道过。当时我们简单说了一下K-fold Cross Validation (K折交叉验证)的技术。
我们这里再来对Cross Validation做一下简单的说明。

已知可选的模型集合$M$，我们的第一个任务就是要从M中选择最好的模型。

假设训练集使用S来表示（样本总数n），

如果我们想使用经验风险最小化来度量模型的好坏，那么我们可以这样来选择模型：

1. 使用S来训练每一个$m_i$，训练出参数后，也就可以得到假设函数$h_i$。（比如，线性模型中得到$\theta_i$后，也就得到了假设函数$h_i(\theta) = \theta_i^Tx$）
   • 选择错误率最小的假设函数

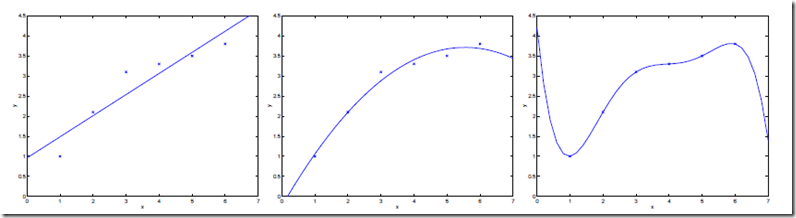
   • 遗憾的是这个算法不可行，因为我们真正需要的是模型对于未知样本的泛化能力。比如我们需要拟合一些样本点，使用高阶的多项式回归肯定比线性回归错误率要小，偏差小，但是方差却很大，会过度拟合。如图：
     

     因此，我们改进算法如下：

     1. 从全部的训练数据S中随机选择70%的样例作为训练集$S_{train}$，剩余的30%作为测试集$S_{cv}$。
     2. 在$S_{train}$上训练每一个$m_i$，得到假设函数$h_i$。
     3. 在$S_{cv}$上测试每一个$h_i$，得到相应的经验错误$\hat{\varepsilon}_{S_{cv}}(h_i)$。
     4. 选择具有最小经验错误$\hat{\varepsilon}_{S_{cv}}(h_i)$的$h_i$作为最佳模型。

     这种方法称为hold-out cross validation或者称为简单交叉验证。

     由于我们将测试集与训练集进行了分割，训练过程中没有测试集的参与，因此我们可以认为这里由测试集得到的$\hat{\varepsilon}_{S_{cv}}(h_i)$远比训练集得到的最小经验误差更能表现泛化误差（generalization error）。这里测试集的比例一般占全部数据的1/4-1/3。30%是典型值。

     到这里看起来已经选出一个令人满意的模型了，实际上还可以进一步优化我们的模型，当选出最佳的模型$h_i$后，再在模型$h_i$上用全部数据$S$上做一次训练，显然训练数据越多，模型参数越准确。

     这里需要说明一个简单交叉验证方法不足点：即使我们采取了上面说道的优化方法，我们的最优模型依然是在浪费了30％数据的前提下选择的。不能证明在全部训练数据上是最佳的。在样本量很丰富的情况下，这样做没有任何问题，但当我们的样本非常稀少时（比如，n = 20）再分出测试集后，训练数据就太少了。

     我们现在对简单交叉验证方法再做一次改进，如下：

     1. 将训练集$S$随机分成k个不相交的子集，得到相应的子集{$s_1,s_2,...s_k$}，每个子集大小为n/k。
        • 每次从模型集合$M$中拿出来一个$m_i$，然后在训练子集中选择出1个$s_j$用作测试集，将剩下的k-1个子集拿来对$m_i$进行训练，得到$h_{ij}$.最后在$s_j$上得到$\hat{\varepsilon}_{S_{cv}}(h_{ij})$.
          $s_j$的选择可以有k个，当我们对这k种情况分别计算得到对应的$\hat{\varepsilon}_{S_{cv}}(h_{ij})$，最后取k次的平均值作为训练以后的模型的泛化误差。
        • 选出平均泛化误差最小的$m_i$，然后使用全部的$S$再做一次训练，得到最后的$h_i$。

     这个方法称为k-fold cross validation（k-折叠交叉验证）。简单点讲，这个方法就是将简单交叉验证的测试集改为1/k，每个模型训练k次，测试k次，错误率为k次的平均。一般讲k取值为10。这样数据稀疏时基本上也能进行。显然，缺点就是训练和测试次数过多。
     极端情况下，k可以取值为n，意味着每次留一个样例做测试，这个称为leave-one-out cross validation。

     可以看到，我们可以将cross validation用于模型的选择。
     

     特征选择（Feature selection）

     特征选择严格来说也是模型选择中的一种。假设我们想对维度为n的样本点进行回归，但n很大(n>>m)。这时，我们认为学习目标只和少量的特征是相关的，在这样的条件下，我们可以应用特征选择算法来剔除n中一部分特征。n个特征，考虑每个特征的去留问题，就会产生$2^n$种可能性。如果我们枚举这些情况，然后利用交叉验证逐一考察在该情况下模型的平均泛化误差，不大现实。所以一般我们会采取一些启发式搜索方法。

     前向搜索(Forward Search )

     　算法描述：特征子集X从空集开始，每次选择一个特征x加入特征子集X，使得特征函数$J(X)$最优。简单说就是，每次都选择一个使得评价函数的取值达到最优的特征加入，其实就是一种简单的贪心算法。
     　算法评价：缺点是只能加入特征而不能去除特征。例如：特征A完全依赖于特征B与C，可以认为如果加入了特征B与C则A就是多余的。假设序列前向选择算法首先将A加入特征集，然后又将B与C加入，那么特征子集中就包含了多余的特征A

     1. 初始化特征集$F=\emptyset$。
     2. 扫描i从1到n，
        如果第i个特征不在$F$中，令$F_i = F\bigcup\lbrace{i}\rbrace$
        利用交叉验证来得到在$F_i$下模型的平均泛化误差。
     3. 令$F=min(F_i\in\lbrace{F_1,F_2,...F_n}\rbrace)$。
     4. 如果F中的特征数达到了n或者预设定的阈值（如果有的话），没达到转到2,最后输出整个搜索过程中最好的$F$.

     前向搜索属于wrapper model feature selection。Wrapper这里指不断地使用不同的特征集来测试学习算法。前向搜索说白了就是每次增量地从剩余未选中的特征选出一个加入特征集中，待达到阈值或者n时，从所有的F中选出错误率最小的。

     除了前向搜索，自然也有后向搜索(Backward Search )。$F$预设值$\lbrace{1,2,..,n}\rbrace$，然后每次删除一个特征，并评价，直到达到阈值或者为$\emptyset$，最后选择最佳的$F$。

     这两种算法都可以工作，但是计算复杂度比较大。时间复杂度为$O(n^2)$。

     过滤特征选择（Filter feature selection）

     过滤特征选择方法的思想是针对每一个特征$x_i$，i从1到n，计算$x_i$相对于类别标签$y$的信息量$S(i)$，得到n个结果，最后我们输出k个拥有最大的$S(i)$的对应特征。显然，这样复杂度大大降低，为$O(n)$。

     那么关键问题就是使用什么样的方法来度量$S(i)$?

     一种可行的选择是通过在训练集中计算，把$x_i$与y的关联度定义为$S(i)$。这样做的话，我们会得到k个跟y的关联度最高的特征。实际使用中（$x_i$表现为离散分布）我们把$x_i$与y之间的互信息$MI(x_i,y)$作为$S(i)$:

     互信息（Mutual information）公式：
     

     $$MI(x_i,y)=\sum_{x_i\in\lbrace{0,1}\rbrace}\sum_{y\in\lbrace{0,1}\rbrace}p(x_i,y)log\frac{p(x_i,y)}{p(x_i)p(y)}$$
     等式认为 $x_i$和y都是二值型的，更一般的，我们可以推广到多个离散值的情况。（ $p(x_i,y),p(x_i),p(y)$都是从训练集上得来的）

     我们需要明白这个关联度函数是怎嘛来的，这里的$MI(x_i,y)$可以有另一种表述KL距离（Kullback-Leibler）：

     $$MI(x_i,y)=KL(p(x_i,y)||p(x_i)p(y))$$

     简单来说，$MI(x_i,y)$衡量的是$p(x_i,y)$与$p(x_i)p(y)$概率分布的差异性。如果$x_i$和y是独立随机变量，我们将得到$p(x_i,y)＝p(x_i)p(y)$，也就是说KL距离值为0，也就是说$x_i$和y不相关。相反，如果两者密切相关，那么MI值会很大。
     在对$MI(x_i,y)$进行排续后，接下来我们的问题就是如何选择k值。标准做法是选择一种交叉验证的方法开选择可能的k值（将k从1扫描到n，取最大的F。不过这次复杂度是线性的了）。举例来手，当我们应用朴素贝叶斯进行文本分类时，整个词汇表可能很大——使用过滤特征选择算法来选择特征子集进行分类操作，经常能够提高分类器的精度。

     贝叶斯统计和规则化（Bayesian statistics and regularization）

     这一部分，我们要来介绍一种可以减少过度拟合情况的技术。

     我们先来谈谈之前利用最大似然估计（ML）的方法来选择参数的式子：
     

     $$\theta_{ML}=arg \max_{\theta}\prod_{i=1}^mp\left(y^{(i)}|x^{(i)};\theta\right)$$

     维基百科将样本（观察数据）记为$X$，然后求$P(X)$的最大概率。然而，对于我们这里的样本而言，分为特征$x$和类标签y。我们需要具体计算$P(X)$。在判别模型（如logistic回归）中，我们认为$P(X)=P(x,y)=P(y|x)P(x)$，而$P(x)$与$\theta$独立无关，因此最后的$arg \max_{} P(X)$由$arg \max_{}P(y|x)$决定，也就是上式$\theta_{ML}$。严格来讲$\theta_{ML}$并不等于样本$X$的概率，只是$P(X)$决定于$\theta_{ML}$，$\theta_{ML}$最大化时$P(X)$也最大化。在生成模型，如朴素贝叶斯中，我们认为$P(X)=P(y)P(x|y)$，也就是在某个类标签y下出现特征x的概率与先验概率之积。而$P(x|y)$在x的各个分量是条件独立情况下可以以概率相乘形式得出，这里根本没有参数$\theta$。因此最大似然估计直接估计$P(x,y)$即可，变成了联合分布概率。

     在上式中，我们认为参数$\theta$为未知的。

     • 统计学派（frequentist statistics）认为$\theta$是未知常量。统计学派认为$\theta$不是随机变量，只是一个未知的常量。因此，我们没有把$p\left(y^{(i)}|x^{(i)};\theta\right)$写成$p\left(y^{(i)}|x^{(i)},\theta\right)$。我们的任务就是就是利用统计学方法（比如最大似然估计）来评估这个未知常量。
     • 另一种视角称之为贝叶斯学派（Bayesian），他们提供了另一种解决我们的参数评估问题的方法。他们认为$\theta$是未知的随机变量。这种角度下$\theta$为随机变量，那么不同的$\theta$值就有了不同的先验分布$p(\theta)$（称为先验概率）。我们将训练集表示成$S=\lbrace{\left(x^{(i)},y^{(i)}\right)}\rbrace^m_{i=1}$。当我们需要对新的样本$x$做出预测时，我们可以先求出$\theta$的后验概率分布:

     $$\begin{align} p(\theta|S) & = \frac{p(S|\theta)p(\theta)}{p(S)} \tag 1 \\ & = \frac{\left(\prod_{i=1}^mp\left(y^{(i)}|x^{(i)},\theta\right)\right)p(\theta)}{\int_\theta\left(\left(\prod_{i=1}^mp\left(y^{(i)}|x^{(i)},\theta\right)\right)p(\theta)\right)\,d\theta} \tag 2 \\ \end{align}$$

     根据贝叶斯公式可以得到第一步。再来看第二步的分母，分母写成这种形式后，意思是对所有的$\theta$可能值做积分，求得的结果表示为$\prod_{i=1}^mp\left(y^{(i)}|x^{(i)}\right)$。从宏观上理解，就是在求每个样例概率的乘积。根据全概率公式可得

     $$\begin{align} p(S) & =\int_\theta p(S,\theta)\,d\theta \tag 1 \\ & =\int_\theta p(S|\theta)p(\theta)\,d\theta \tag 2 \\ \end{align}$$

     $p\left(y^{(i)}|x^{(i)},\theta\right)$在不同的模型下计算方式不同。比如在贝叶斯logistic回归中，

     $$p\left(y^{(i)}|x^{(i)},\theta\right)=h_\theta\left(x^{(i)}\right)^{y^{(i)}}\left(1-h_\theta\left(x^{(i)}\right)\right)^{1-y^{(i)}}$$
     其中 $h_\theta\left(x^{(i)}\right)＝1/(1+exp(-\theta^Tx^{(i)}))$

     当有一个新来样例$x$需要预测时，我们可以通过$theta$的后验概率来计算y的后验概率：

     $$p(y|x,S)=\int_\theta p(y|x,\theta)p(\theta|S)\,d\theta$$

     $p(\theta|S)$可以由前面的公式得到。如果我们要求给定$x$情况下的y的期望值，那么套用期望公式即可：

     $$E[y|x,S]=\int_\theta yp(y|x,S)\,dy$$

     我们上面做的工作可以被认为是完全贝叶斯预测，可以看到，这里求解预测$p(y|x,S)$的方式与之前的方式不同，以前是先求$\theta$，然后直接预测y，这里需要对所有可能的$\theta$做积分。

     再总结一下两者的区别:

     • 最大似然估计没有将$\theta$视作y的估计参数，认为$\theta$是一个常数，只是未知其值而已，比如我们经常使用常数c作为$y=2x+c$ 的后缀一样。但是$p(y|x;\theta)$的计算公式中含有未知数$\theta$。所以再对极大似然估计求导后，可以求出$\theta$。
     • 而贝叶斯估计将$\theta$视为随机变量，$\theta$的值满足一定的分布，不是固定值，我们无法通过计算获得其值，只能在预测时计算积分。

     然而在上述贝叶斯估计方法中，虽然公式合理优美，但后验概率$p(\theta|s)$却很难计算，看其公式知道计算分母时需要在所有的$\theta$上作积分，然而对于一个高维的$\theta$来说，枚举其所有的可能性复杂度过高。

     为了解决这个问题，我们需要改变思路。看$p(\theta|s)$公式中的分母，分母其实就是$P(S)$，而我们就是要让$P(S)$在各种参数的影响下能够最大（这里只有参数$\theta$）。因此我们只需求出随机变量$\theta$中最可能的取值，这样求出$\theta$后，可$\theta$视为固定值，那么预测时就不用积分了，而是直接像最大似然估计中求出$\theta$后一样进行预测，这样就变成了点估计。这种方法称为最大后验概率估计$MAP$（Maximum a posteriori）方法:

     $$\theta_{MAP}=arg\max_{\theta}\prod_{i=1}^mp\left(y^{(i)}|x^{(i)},\theta\right)p(\theta)$$

     $\theta_{ML}$与$\theta_{MAP}$一样表示的是$P(S)$，意义是在从随机变量分布中以一定概率$p(\theta)$选定好$\theta$后，在给定样本样本$(x^{(i)},y^{(i)})$出现的概率积。

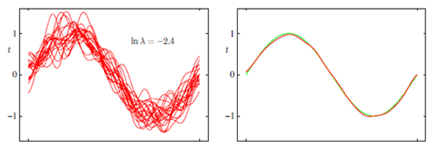
     与最大似然估计对比发现，MAP只是将$\theta$移进了条件概率中，并且多了一项$p(\theta)$。一般情况下我们认为$\theta满足N(0,\,\tau^{2}I)$，实际上，贝叶斯最大后验概率估计相对于最大似然估计来说更容易克服过度拟合问题。我想原因是这样的，过度拟合一般是极大化$p(y^{(i)}|x^{(i)};\theta)$造成的。而在$\theta_{ML}$中，整个公式由两项组成，极大化$p(y^{(i)}|x^{(i)}，\theta)$时，不代表此时$p(\theta)$也能最大化。相反，$\theta$是多值高斯分布，极大化$p(y^{(i)}|x^{(i)}，\theta)$时，$\theta$概率反而可能比较小。因此，要达到最大化$\theta_{ML}$需要在两者之间达到平衡，也就靠近了偏差和方差线的交叉点。当我们在贝叶斯logistic回归（使用$\theta_{ML}$的logistic回归）应用于文本分类时，即使特征个数n远远大于样例个数m，也很有效。