树
树的定义
树是由一个集合以及在该集合上定义的一种关系构成的,集合中的元素称为树的结点,所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构,在这种层次结构中有一个结点具有特殊的地位,这个结点称为该树的根结点。
数据结构中有很多树的结构,其中包括二叉树、二叉搜索树、2-3树、红黑树等等,本文着重介绍二叉树。
树的基本术语
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 叶节点或终端节点:度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的存储结构
双亲表示法

孩子表示法

二叉树
二叉树是数据结构中一种重要的数据结构,也是树表家族最为基础的结构。
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
二叉树的性质
- 二叉树的第 i i i层至多有 2 i − 1 2^{i-1} 2i−1 个结点;
- 深度为 k k k 的二叉树至多有 2 k − 1 2^k-1 2k−1 个结点;
- 对任何一棵二叉树 T T T ,如果其终端结点数为 n 0 n_0 n0 ,度为2的结点数为 n 2 n_2 n2 ,则 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1 。
二叉树的实现
结构
template <class DataType>
struct BiNode
{
DataType data;
BiNode<DataType> * lchild,*rchild;
};
template <class DataType>
class BiTree
{
public:
BiTree(){root = Create(root);}
~BiTree(){Release(root);}
void PreOrder(){PreOrder(root);} //前序遍历
void InOrder(){InOrder(root);} //中序遍历
void PostOrder(){PostOrder(root);} //后序遍历
private:
BiNode<DataType> * root;
BiNode<DataType> * Create(BiNode<DataType> *bt);
void Release(BiNode<DataType> *bt);
void PreOrder(BiNode<DataType> *bt);
void InOrder(BiNode<DataType> *bt);
void PostOrder(BiNode<DataType> *bt);
};
建立二叉树
template <class DataType>
BiNode<DataType> *BiTree<DataType>::Create(BiNode<DataType> *bt)
{
DataType ch;
cin>>ch;
if(ch == '#') bt = NULL;
else{
bt = new BiNode<DataType>;
bt->data = ch;
bt->lchild = Create(bt->lchild);
bt->rchild = Create(bt->rchild);
}
return bt;
}
释放二叉树
template <class DataType>
void BiTree<DataType>::Release(BiNode<DataType> *bt)
{
if(bt != NULL){
Release(bt->lchild);
Release(bt->rchild);
delete bt;
}
}
前序遍历
template <class DataType>
void BiTree<DataType>::PreOrder(BiNode<DataType> *bt)
{
if(bt == NULL) return;
else{
cout<<bt->data;
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
中序遍历
template <class DataType>
void BiTree<DataType>::InOrder(BiNode<DataType> *bt)
{
if(bt == NULL) return;
else{
InOrder(bt->lchild);
cout<<bt->data;
InOrder(bt->rchild);
}
}
后序遍历
template <class DataType>
void BiTree<DataType>::PostOrder(BiNode<DataType> *bt)
{
if(bt == NULL) return;
else{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout<<bt->data;
}
}
满二叉树
一棵深度为k且有 2 k − 1 2^k-1 2k−1 个结点的二叉树称为满二叉树。
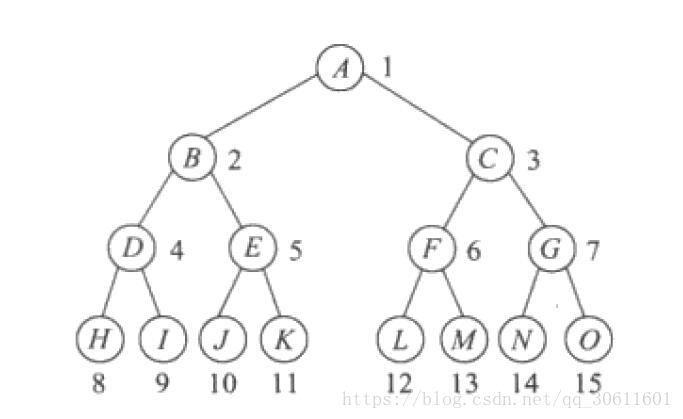
满二叉树的性质:
-
一颗树深度为 h h h ,最大层数为 k k k,深度与最大层数相同, k = h k=h k=h ;
-
叶子数为 2 h 2h 2h ;
-
第k层的结点数是: 2 k − 1 2^{k-1} 2k−1 ;
-
总结点数是: 2 k − 1 2^k-1 2k−1 ,且总节点数一定是奇数。
完全二叉树
深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树。
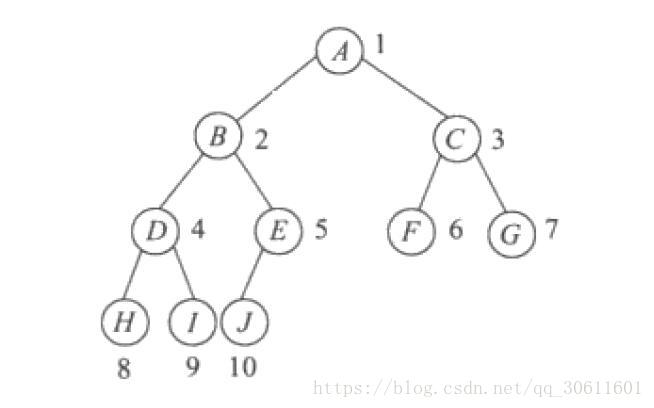
**注:**完全二叉树是效率很高的数据结构,堆是一种完全二叉树或者近似完全二叉树,所以效率极高,像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化,二叉排序树的效率也要借助平衡性来提高,而平衡性基于完全二叉树。
二叉排序树
二叉查找树定义:又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 它的左、右子树也分别为二叉排序树。
平衡二叉树
平衡二叉树(Balanced Binary Tree)又被称为AVL树。它或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。(注:平衡二叉树应该是一棵二叉排序树)
欢迎支持
淘宝搜券小助手上线啦,喜欢网购的你赶快来试试吧~!淘宝搜券微信机器人正在开发中,尽情期待!点击链接进入→淘宝搜券小助手


























 1595
1595

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










