1.4卷积神经网络笔记—Padding

1.边缘检测的缺点

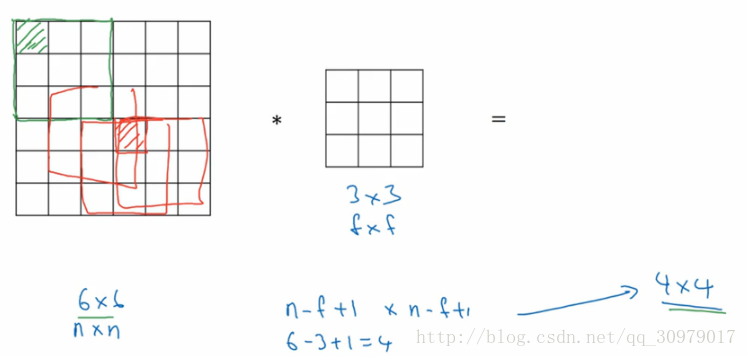
6*6矩阵与3*3矩阵卷积，得到4*4矩阵。普遍规律是  n*n 卷积 f*f 得到 n-f+1 * n-f+1。

但是存在两个缺点：

1.卷积后的矩阵越变越小（如果卷积层100层，每一层都缩小最终得到的将是很小的图片）

2.输入矩阵（左）边缘像素（绿阴影）只被计算过一次，而中间像素（红阴影）被卷积计算多次，意味着丢失图像角落信息。

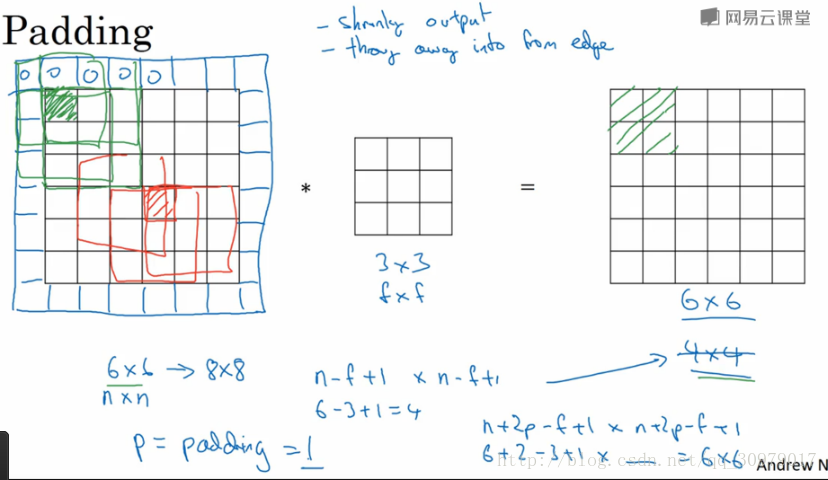
为了解决这两个问题，就对输入图像进行padding，即填充像素

2.利用padding解决上述缺点

eg1：

上图将输入图像矩阵周围填充一层像素（通常填充元素为0）填充数量p=1，输出图像大小变为n+2p-f+1 * n+2p-f+1，6*6——>8*8，卷积输出为6*6，与原输入图像大小相同，解决了卷积会使图片变小的缺点。（当然也可以填充两层）；输出矩阵绿色阴影块是受输入矩阵绿色阴影值影响的部分，削弱了边缘信息丢失的缺点。

3.valid和same两种卷积方法

valid卷积：不填充

same卷积：填充后（p），输入（n*n）输出（n+2p-f+1 * n+2p-f+1）大小相同：

，即f为奇数时，填充数量p根据上式计算。

通常计算机视觉使用的滤波器矩阵f都是奇数。（可能是由于奇数f使p填充时对称；奇数f使滤波器矩阵有中心像素点，计算机视觉中方便指出滤波矩阵位置）