[论文阅读] Complex Embeddings for Simple Link Prediction

pdf：http://proceedings.mlr.press/v48/trouillon16.pdf
code：https://github.com/ttrouill/complex
[ICML2016]

知识图谱可以看作是清洗过的知识库，包含实体、关系，其中实体包括头实体和尾实体。利用表示学习方法可以将实体、关系嵌入到低维实值向量中，并捕捉实体及关系中的复杂语义关系。这篇文章解决的是关系预测问题。

模型

二进制单一关系

a single type of relation

在两个实体之间的关系可以用一个二进度值来表示（不是1就是-1）：

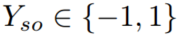
它的概率值可以用下述函数得到，比如当值为1的时候：

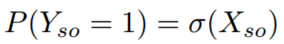
其中X是分数的潜在矩阵（维度是n×n，表示实体与实体之间的关系分数），Y是部分可观察的符号矩阵。

关系预测任务可以看作是矩阵补全任务，在目前的这个分数的潜在矩阵中，有一部分是可观察到的，另一部分是不可观察到的，现在我们的目的就是把这个矩阵补全。因此现在X是不完整的，我们希望可以找到一个更通用的结构来找到X的近似，从而进行补全。

标准的矩阵分解方法会把X进行分解，通过一个矩阵乘法：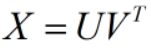
但是，其中的U和V是两个不同的n×K的矩阵，K是矩阵的秩（可以理解为分解的潜在因子K个）。但是在知识图谱中，同样的一个实体，作为头实体和尾实体，虽然位置不同，但是它本质是同一个实体，我们希望得到的低维向量表示是一样的，但是标准的矩阵分解方法得到的确实不一样的向量表示（作为头实体和尾实体）。

然后提到了奇异值分解（SVD），并说一般的解决方法是共享左右因子的嵌入（我理解的是将作为头实体、尾实体，得到的不一样的向量表示，比如平均啊之类的，让它们相同并共享。

然后提到将点积转为评分函数，比如还有合成函数，用一种特殊的方式将嵌入（embeddings）进行结合（combine），（从而让它们一致）。
并列举了一些模型的评分矩阵：

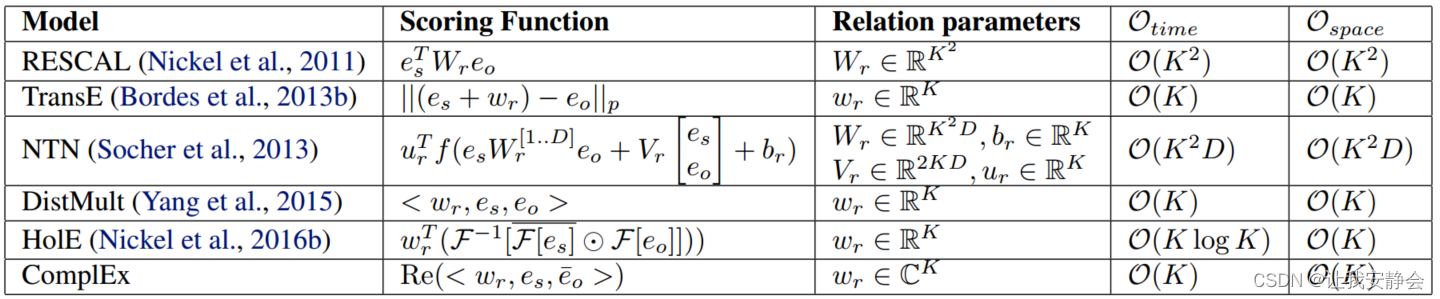
还有的方法用特征值分解的方法来让左右因子一致：

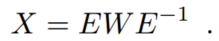
但是这个方法要求X是一个对称矩阵（或者接近对称），并举例有哪些矩阵式满足的。在这些情况下，分解得到的E是正交的，因此得到的左右因子是相等的。

在这篇文章中，作者关心的是那些非对称的关系，即在矩阵中表现为非对称的矩阵，在这种情况下，上述说的特征值分解的方法，分解得到的结果将不可能出现在实空间中，得到的结果将出现在复空间中，其中的嵌入（embeddings）包含两个部分：实部Re(x)和虚部Im(x)。（因此分别称为实向量和虚向量）

• real space 实空间（包含的值是实值）
• complex space 复空间（包含的值是复数，包含实部和虚部）

对于复数的点积，定义为：

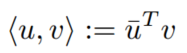
其中的u和v都是复数（包含实部和虚部）。然后由于复数特征向量的特征分解的计算量太大，过于复杂，产生计算量的问题。数学中可以通过求特征向量矩阵的逆来进行近似，因此考虑正规矩阵的空间。比如一个复数矩阵X（维度为n×n），于是：

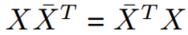
正规矩阵的谱定理表明一个矩阵X是正规的当且仅当它是酉可对角化的：

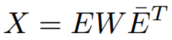
其中，W是特征值的对角矩阵，E是特征向量的单式矩阵，E横线 是特征向量的复共轭。
纯实数的正规矩阵集包括所有对称和反对称符号矩阵、以及所有的正交矩阵，以及还有很多其他的矩阵可以表示二元关系。但是把所有的矩阵都像上述那样表示是复杂的，因此本文在分解过程中，只保留复数的实部：

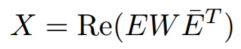
事实上，在实空间上执行这个投影可以精确分解任何实方阵X（对称不对称的都可以）

因此，相比于奇异值分解（SVD），特征值分解有两点不同：

1. 特征值不需要一定是正数或者实数；
2. 对于上式而言，E的行和列可以对应到关系矩阵X的行和列。对于某一个实体而言，它的头实体嵌入向量（subject embedding vector）就是它的尾实体嵌入向量（object embedding vector）的共复轭。

低秩分解

pass

二进制多关系

Binary Multi-Relational Data

将单一关系扩展到多关系。
本文通过在所有关系中分享实体关系，将一个嵌入（embeddings）分配给一个关系，想通过所有的关系来恢复分数Xr的分数，事实为真（Y=1）的概率：

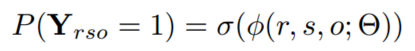
X作为整体是未知的，但是可以观察到事实是真（=1）或假（=-1），相对应的不同部分观察到的相邻矩阵具有不同的关系。因此，对于一系列具有不同未观察到的三元组而言，就是去判断概率是真还是假，根据不同的评分函数，模型是不同的，本文的评分函数为：

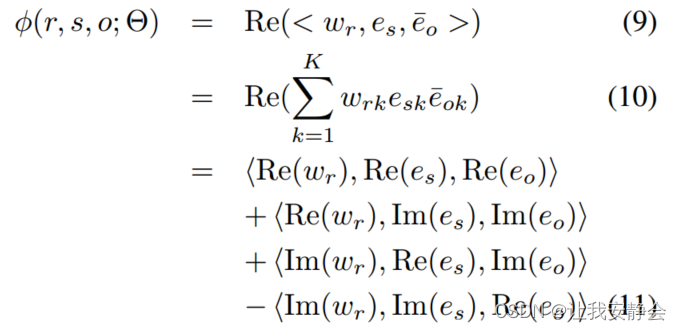
上述（10）对应DistMult with 实嵌入，但是由于其中一个嵌入的复共轭，可以处理不对称的情况。

上述（11）只涉及嵌入关系实部和虚部对应的实向量。

参考：

1. Complex Embeddings for Simple Link Prediction：https://zhuanlan.zhihu.com/p/107914673
2. 论文浅尝 | Complex Embeddings for Simple Link Prediction：https://blog.csdn.net/tgqdt3ggamdkhaslzv/article/details/79081541
3. 复数的物理意义是什么？：https://www.zhihu.com/question/23234701/answer/27293131