Level Set 由应用数学家 Osher 于 1988 年提出,最早用于计算物理中对界面的捕捉。
Active Contour Model(ACM) 将分割问题看作了能量最小化问题,Curve Evolution(曲线演化) 就是 ACM 实现分割任务的方法,而 Level Set Method(水平集方法) 是实现曲线演化的方法。
Ⅰ. Active Contour Model
1988年,Kass 等人提出了 Active Contour Model(ACM,主动轮廓模型),将图像分割问题转换为 求解能量泛函最小值问题。
ACM 的基本思想: 使用连续曲线表达目标轮廓,定义一个关于轮廓曲线的能量泛函,通过求解能量函数对应的欧拉方程,使得能量达到最小时的曲线位置就是目标轮廓的所在位置,因此分割过程就转变为了求解能量泛函最小值的过程。
ACM 的主要原理: 通过构造能量泛函,在能量函数最小值的驱动下,让轮廓曲线逐渐向待检测物体的边缘逼近,最终分割出目标。
Active Contour Model 是当前应用最多的利用 变分思想 求解的图像分割方法。其最大优点是在高噪声的情况下,也能得到连续、光滑的闭合分割边界。
【变分法】变分法属于泛函分析领域,在普通的最优化问题中,往往求解得到的是一个最优值解,而在一个变分问题中,求解得到的是一个最优函数解,因此变分问题可以看成是泛函的极值问题
=====================================================================================
概念一:ACM 的轮廓表示
由于 Active Contour Model 利用曲线演化来定位目标的边缘,因此也称为 Snake 模型。
Active Contour Model 按照 能量函数构造方式 的不同,主要分为 基于边缘 和 基于区域 两类,同时也有一些工作提出了将基于边缘和区域相结合的 Active Contour Model。
Active Contour Model 方法的关键就在于:
- 轮廓应该如何表示?
- 促使轮廓变化的力应该如何构造?
对于轮廓如何表示这个问题,形成两大流派:
1. 参数活动轮廓模型(parametric active contour model)
轮廓曲线是由参数表示的,典型代表为 Snake 模型。Snake 也叫基于边缘的活动轮廓模型,主要是根据目标边缘的梯度跳变来检测目标。
Snake 的具体作法是:
- 先在图像创建一条初始轮廓,形状不拘,但 需要将目标物体轮廓线包含在初始轮廓在内侧 ;
- 接着建立 “能量方程”,方程包括了以规范曲线形状为目的 “内部能量”,以规范曲线与目标物体轮廓线接近程度为目的的 “外部能量”
- 在运算过程中,最小化内部能量可令曲线 持续向内部收缩并保持平滑,最小化外部能量则可令曲线 持续贴近目标物体轮廓线直到重合为止
Snakes 模型在计算机视觉中被普遍使用,并且引发了 2D 和 3D 领域的一些改进。
2. 几何活动轮廓模型(geomeric active contour model)
轮廓曲线是几何表示的,典型代表为 Level Set Method。
基于边缘的 Snake 模型存在的问题是需要将曲线进行参数化,这是不容易的,而且 Snake 还不善于处理曲线的拓扑变换,比如在演化前是相邻的点,演化后非相邻点,用直接处理曲线的方式很难实现,而 Level Set Method 可以实现复杂的拓扑结构变化。
对于如何构造力的问题,是两个流派都遇到的问题。
=====================================================================================
概念二:曲线演化理论
曲率力:
曲线曲率(curvature)是针对曲线上某个点的切线方向角对弧长的转动率,通过微分定义,表明了 曲线偏离直线的程度。曲率越大表示曲线的弯曲程度越大,曲率的倒数就是曲率半径。
通常规定,凸面的曲率为正,凹面的曲率为负。(其实要反过来也可以,曲率的正负只是为了区分曲面的凹向,但习惯上是这么规定的)
凸面:过面上任意一点做切面,表面总是在切面的下方

凹面:过面上任意一点做切面,表面总是在切面的上方

曲线存在曲率,曲率有正有负,于是在法向曲率力的推动下,曲线的运动方向之间有所不同:有些部分朝外扩展,而有些部分则朝内运动。下面蓝色箭头曲率为负,绿色箭头曲率为正:

简单曲线在曲率力(也就是曲线的二次导数)的驱动下演化所具有的一种非常特殊的数学性质是:一切简单曲线,无论被扭曲得多么严重,只要还是一种简单曲线,那么在曲率力的推动下最终将退化成一个圆,然后消逝(可以想象下,圆的所有点的曲率力都向着圆心,所以它将慢慢缩小,以致最后消逝)
=====================================================================================
概念二:ACM发展
1. Snake
Snake 模型就是一条 可变形的参数曲线 及 相应的能量函数,以最小化能量目标函数为目标,控制参数曲线变形,具有最小能量的闭合曲线就是目标轮廓。
Snake模型首先需要在感兴趣区域的附近给出一条初始曲线,接下来最小化能量泛函,让曲线在图像中发生变形并不断逼近目标轮廓。
Kass等提出的原始Snakes模型由一组控制点:v(s)=[x(s), y(s)] s∈[0, 1] 组成,这些点首尾以直线相连构成轮廓线。其中x(s)和y(s)分别表示每个控制点在图像中的坐标位置。 s 是以傅立叶变换形式描述边界的自变量。在Snakes的控制点上定义能量函数(反映能量与轮廓之间的关系):
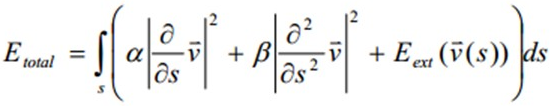
其中第1项称为弹性能量是v的一阶导数的模,第2项称为弯曲能量,是v的二阶导数的模,第3项是外部能量(外部力),在基本Snakes模型中一般只取控制点或连线所在位置的图像局部特征例如梯度:

也称图像力。(当轮廓C靠近目标图像边缘,那么C的灰度的梯度将会增大,那么上式的能量最小,由曲线演变公式知道该点的速度将变为0,也就是停止运动了。这样,C就停在图像的边缘位置了,也就完成了分割。那么这个的前提就是目标在图像中的边缘比较明显了,否则很容易就越过边缘了。)
弹性能量和弯曲能量合称内部能量(内部力),用于控制轮廓线的弹性形变,起到保持轮廓连续性和平滑性的作用。而第三项代表外部能量,也被称为图像能量,表示变形曲线与图像局部特征吻合的情况。内部能量仅仅跟snake的形状有关,而跟图像数据无关。而外部能量仅仅跟图像数据有关。在某一点的α和β的值决定曲线可以在这一点伸展和弯曲的程度。
最终对图像的分割转化为求解能量函数Etotal(v)极小化(最小化轮廓的能量)。在能量函数极小化过程中,弹性能量迅速把轮廓线压缩成一个光滑的圆,弯曲能量驱使轮廓线成为光滑曲线或直线,而图像力则使轮廓线向图像的高梯度位置靠拢。基本Snakes模型就是在这3个力的联合作用下工作的。
因为图像上的点都是离散的,所以我们用来优化能量函数的算法都必须在离散域里定义。所以求解能量函数Etotal(v)极小化是一个典型的变分问题(微分运算中,自变量一般是坐标等变量,因变量是函数;变分运算中,自变量是函数,因变量是函数的函数,即数学上所谓的泛函。对泛函求极值的问题,数学上称之为变分法)。
在离散化条件(数字图像)下,由欧拉方程可知最终问题的答案等价于求解一组差分方程:(欧拉方程是泛函极值条件的微分表达式,求解泛函的欧拉方程,即可得到使泛函取极值的驻函数,将变分问题转化为微分问题。)
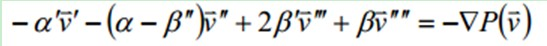
记外部力 F = −∇ P, Kass等将上式离散化后,对x(s)和y(s)分别构造两个五对角阵的线性方程组,通过迭代计算进行求解。在实际应用中一般先在物体周围手动点出控制点作为Snakes模型的起始位置,然后对能量函数迭代求解。
snake的缺点是:能量方程依赖于曲线方程的参数化,不是曲线的本征(intrinsic)表示。因此不能处理变形过程中的拓扑变化,从而不能用于检测多目标的情况。
针对 Snake 模型的缺点,提出改进模型:几何活动轮廓模型
基本思想是将图像按照曲线量化为level set函数(最常用的是signed distance function)。level-set类似于等势线,一幅图像上所有level-set值等于某个常量的点构成一个闭合曲线。
这样的曲线表示方法不依赖于参数化,因此是曲线的本征表示。
运动方程中同样包含了内部能量和外部能量,用于规范曲线形状和吸引曲线到目标位置,与 Snake 模型不同的是,这两项是相乘关系
内部能量定义为了 Level Set 运动的基本速度,其值是 曲线上各点的曲率,它同时具有 Snake 模型中弹性能量和弯曲能量的作用
外部能量定义为图像上梯度值的单调递减函数,当曲线运动到目标边缘时,该项减小,使得曲线停止在目标边缘处
该模型的缺点:曲线停止在目标边缘的条件是运动到边缘时速率为0,而这只在理想情况下才出现。因此曲线容易越过边界运动到物体内部。
继续改进:在第二种模型的基础上进行了改进,使得曲线可以停止在目标物体边缘
Geodesic Active Contours(GAC)
其摒弃了snake对参数的依赖,并加入了水平集,使得轮廓曲线更贴近目标物的拓扑结构
GAC 指出经典 ACM 能量表达中,第二项对分割结果影响不大,即 β \beta β 可以为 0
整体来说:
GAC模型借用了水平集,结合经典的active contour 模型,以图像的梯度为驱动力,在图像梯度最大处,达到收敛。其解决了传统的AC不能处理变形过程中拓扑的变化,如不能处理多物体检测,以及需要对参数的预设置等问题。但是,其在处理模糊图像,或者纹理图像时,效果还是不理想。
=====================================================================================
概念三:能量函数
Active Contour 是图像上一组排序点的集合,可以表示为:
V
=
{
v
1
,
v
2
,
.
.
.
,
v
L
}
V = \{v_1, v_2, ..., v_L\}
V={v1,v2,...,vL}
其中,
v
i
=
(
x
i
,
y
i
)
,
i
=
{
1
,
2
,
.
.
.
,
L
}
v_i = (x_i, y_i),i= \{1,2,...,L\}
vi=(xi,yi),i={1,2,...,L},代表轮廓上的每一个点,所以对轮廓上的每个点可以通过求解最小能量问题来迭代地逼近目标边界,对每个轮廓点
v
i
v_i
vi 邻域中的点
v
′
v'
v′,有能量函数:
E
i
(
v
i
′
)
=
α
E
i
n
t
(
v
i
′
)
+
β
E
e
x
t
(
v
i
′
)
E_i(v_i') = \alpha E_{int}(v_i') + \beta E_{ext}(v_i')
Ei(vi′)=αEint(vi′)+βEext(vi′)
- E i n t E_{int} Eint 内部能量函数:与曲线轮廓自身有关(如尺寸、形状等)和图像数据无关,推动轮廓形状的改变并保持轮廓上点间的距离
- E e x t E_{ext} Eext 外部能量函数:与图像数据有关(如灰度、梯度等),将曲线向感兴趣的特征(如边缘)吸引构建能量函数
- α \alpha α 和 β \beta β 为加权常数,决定曲线在这一点伸展和弯曲的程度
v i v_i vi 是当前轮廓上的一个点, v i ′ v_i' vi′ 是根据能量项所能确定的 v i v_i vi 能量最小的位置。在迭代的逼近过程中,当前轮廓上的每个点 v i v_i vi 都会移动到对应 E i ( ⋅ ) E_i(·) Ei(⋅) 最小值的位置点 v i ′ v_i' vi′,如果能量函数选择恰当,通过不断的迭代和逼近,最终轮廓应该停在实际的目标轮廓上(对应最小能量位置)。
初始轮廓点逼近目标边界过程:

小结: 内部力(能量)和外部力(能量)的作用不同,内部力起平滑约束作用,外部力引导曲线向图像特征移动。
在能量函数极小化过程中,弹性能量(内部力)迅速把轮廓线压缩成一个光滑的圆,弯曲能量(内部力)驱使轮廓线成为光滑曲线或直线,而图像力(外部力)则使轮廓线向图像的高梯度位置靠拢。Snakes 模型就是在这三个力的联合作用下工作的。
总的能量函数定义为:


最终对图像的分割问题转化为求解能量函数
E
t
o
t
a
l
(
v
)
E_{total}(v)
Etotal(v) 的最小值。
由于图像上的点都是离散的,那么用来优化能量函数的算法都必须在离散域里定义,所以求解能量函数 E t o t a l ( v ) E_{total}(v) Etotal(v) 的极小化是一个典型的变分问题
变分法: 微分运算中,自变量一般是坐标等变量,因变量是函数;变分运算中,自变量是函数,因变量是函数的函数,即数学上所谓的泛函。对泛函求极值的问题,数学上称之为变分法。
在离散化条件(数字图像)下,由欧拉方程可知最终问题的答案等价于 求解一组差分方程。欧拉方程是泛函极值条件的微分表达式,求解泛函的欧拉方程,即可得到使泛函取极值的驻函数,将变分问题转化为微分问题。

记外部力
F
=
−
∇
P
F = −∇ P
F=−∇P, Kass 等将上式离散化后,对
x
(
s
)
x(s)
x(s) 和
y
(
s
)
y(s)
y(s) 分别构造两个五对角阵的线性方程组,通过迭代计算进行求解。在实际应用中一般先在物体周围手动点出控制点作为 Snakes 模型的起始位置,然后对能量函数迭代求解。
1. 内部能量函数
内部能量函数的作用: 推动曲线轮廓的弹性形变并保持轮廓上点之间的距离。由于内部能量推动轮廓形状的改变,所以常会和坐标有关。
内部能量包括 连续能量 和 膨胀能量。弹性能量(弹性能量)是 V V V 的一阶导数,可以控制轮廓不会无限制地扩展或收缩,膨胀能量(弯曲能量)是 V V V 的二阶导数,可以限制轮廓中尖的角点和尖刺的出现。
内部能量函数定义如下:
α
E
i
n
t
(
v
i
)
=
c
E
c
o
n
(
v
i
)
+
b
E
b
a
l
(
v
i
)
\alpha E_{int}(v_i) = cE_{con}(v_i) + bE_{bal}(v_i)
αEint(vi)=cEcon(vi)+bEbal(vi)
- E c o n E_{con} Econ 连续能量(切向力):推动轮廓形状的整体改变
- E b a l E_{bal} Ebal 膨胀能量(法向力):推动轮廓膨胀或收缩
- c c c 和 b b b 都是加权系数
在没有其他因素时,连续能量
E
c
o
n
E_{con}
Econ 会迫使不封闭的曲线变成直线,封闭的曲线变成圆环,连续能量
E
c
o
n
E_{con}
Econ 定义为:
E
c
o
n
(
v
i
′
)
=
1
A
(
V
)
∣
∣
v
i
′
−
γ
(
v
i
−
1
+
v
i
+
1
)
∣
∣
2
E_{con}(v_i') = \frac{1}{A(V)}||v_i' - \gamma(v_{i-1} + v_{i+1})||^2
Econ(vi′)=A(V)1∣∣vi′−γ(vi−1+vi+1)∣∣2
其中,归一化因子 A ( V ) = 1 L ∑ i = 1 L ∣ ∣ v i + 1 − v i ∣ ∣ 2 A(V) = \frac{1}{L}\sum_{i=1}^L|| v_{i+1} - v_i ||^2 A(V)=L1∑i=1L∣∣vi+1−vi∣∣2 是轮廓中各点间的平均距离, γ \gamma γ 是加权系数,利用 A ( V ) A(V) A(V) 进行归一化可以使得 E c o n ( v i ) E_{con}(v_i) Econ(vi) 与轮廓上点的尺寸、位置以及各点间的朝向关系无关。
膨胀能量可作用在闭合的初始轮廓上,以强制轮廓在没有外来影响的情况下扩展或收缩。比如构造与图像中各处梯度成反比的自适应膨胀能量。
膨胀能量
E
b
a
l
(
v
i
′
)
E_{bal}(v_i')
Ebal(vi′) 可以表示成一个内积:
E
b
a
l
(
v
i
′
)
=
n
i
⋅
[
v
i
−
v
i
′
]
E_{bal}(v_i') = n_i \cdot [v_i - v_i']
Ebal(vi′)=ni⋅[vi−vi′]
其中,
n
i
n_i
ni 是点
v
i
v_i
vi 处外法线的单位向量,实际应用中
n
i
n_i
ni 可以通过将切线向量
t
i
t_i
ti 旋转 90° 来获得,而切线向量可以表示为:
t
i
=
v
i
−
v
i
−
1
∣
∣
v
i
−
v
i
−
1
∣
∣
+
v
i
+
1
−
v
i
∣
∣
v
i
+
1
−
v
i
∣
∣
t_i = \frac{v_i - v_{i-1}}{||v_i - v_{i-1}||} + \frac{v_{i+1} - v_i}{||v_{i+1} - v_i||}
ti=∣∣vi−vi−1∣∣vi−vi−1+∣∣vi+1−vi∣∣vi+1−vi
初始轮廓如果处于具有均匀灰度的目标内部,借助膨胀能量来推动轮廓变形并向目标边界扩展以避免其停在目标内部。
2. 外部能量函数
外部能量也称外部力,外部能量表示变形曲线与图像局部特征吻合的情况,外部能量函数借助图像性质来吸引轮廓点,一般是图像梯度和灰度,有时也使用目标的尺寸和形状。
外部能量函数定义:
β
E
e
x
t
(
v
i
)
=
m
E
m
a
g
(
v
i
)
+
g
E
g
r
a
d
(
v
i
)
\beta E_{ext}(v_i) = mE_{mag}(v_i) + gE_{grad}(v_i)
βEext(vi)=mEmag(vi)+gEgrad(vi)
- E m a g E_{mag} Emag 图象灰度能量:将轮廓吸引向高或低的灰度区域
- E g r a d E_{grad} Egrad 图象梯度能量:将轮廓推向目标边界
- m m m 和 g g g 是加权系数
1)图像灰度能量:
灰度能量
E
m
a
g
(
v
i
′
)
E_{mag}(v_i')
Emag(vi′) 与对应图像点的灰度值
I
(
v
i
′
)
I(v_i')
I(vi′) 成比例,可取:
E
m
a
g
(
v
i
′
)
=
I
(
v
i
′
)
E_{mag}(v_i') = I(v_i')
Emag(vi′)=I(vi′)
如果 m m m 为正,则轮廓会向低灰度区域移动,反之向高灰度区域移动。
2)图像梯度能量:
图像梯度能量函数将轮廓吸引到目标边界位置。
Ⅱ. Curve Evolution
Curve Evolution:就是让一条曲线慢慢地变成另一条曲线。

想要让曲线变化,直觉上我只要指定曲线上的每一个点的运动方向和运动速度就可以了。所以我可以给每个点都有一个速度,速度的大小和方向决定了曲线将如何运动。
曲线运动速度 可以定义为:
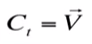
上面是运动方程的简写,其显式表达(Explicit form)应该是:
∂
C
(
p
)
∂
t
=
V
(
p
,
t
)
\frac{\partial C_{(p)}}{\partial t} = V(p,t)
∂t∂C(p)=V(p,t)
即曲线 C C C 对时间 t t t 的偏导数是曲线当前的速度 V V V
其中 :
- C ( p ) C_{(p)} C(p) :表示曲线 C C C 由参数 p p p 定义
- V ( p , t ) V(p,t) V(p,t):速度由参数 p p p 和 t t t 决定,因为速度不仅和曲线有关,还会随着时间变化
举个例子:最开始的黄色曲线经过 t t t 个时刻可能变化成蓝色曲线,再经过 t t t 个时刻又变成了绿色曲线。
曲线形状的改变取决于每一个单独的点的速度,比如为什么绿色曲线最后中部会凸起来,就是曲线上点的速度大小不均匀。

说明:这里的曲线指的是 boundary of shape,可以理解为一个闭合的曲线轮廓,而上面只是截取了其中一小段作为说明。
运动速度 一般是和图像特征有关的(梯度等),比如当前这个点覆盖的区域在图像内部,离分割边界还很远,那么它的速度就会快一点;如果一个点已经很接近分割边界了,那么它的速度就慢下来,甚至最后减小到 0。
运动方向 一般取法线方向,也就是向外扩张的方向,不取切线方向,因为切线方向的力不会改变曲线的形状。
=====================================================================================
概念一:切线分量不影响曲线演化的几何形状
初中物理就学过,任一点上的力
F
F
F 可以分解为切线和法线方向上的分力
F
1
F_1
F1 和
F
2
F_2
F2,同理,在曲线上任意点有一个速度
V
V
V,那么该速度可以分解为该点法线方向(normal direction)和切线方向(tangential direction)的两个分速度。

经过证明,切线方向上的速度不会改变曲线的形状,它只是一个 irrelevant factor,可以借助这句话来理解:The tangential is the velocity you are traveling the curve.( “traveling” 这个词很生动形象)
所以可以将 曲线速度 改写为法线方向上的速度:

其中,
<
V
,
n
>
<V,n>
<V,n> 是速度
V
V
V 投影到法线方向上的分量,
n
n
n 为法线方向的单位向量。此时,
<
V
,
n
>
n
<V,n>n
<V,n>n 就是法线方向的速度,对应上图黑色箭头所指示的。
Q1:切线方向的力为什么不会改变曲线形状?
举一个最极端的例子:一个二维的圆形,每一个点都向着切线方向运动,那么最后的结果脑补一下,就是这个圆滚动起来,但形状并不发生改变。
推广到任意形状的二维曲线,每一个点向切向方向运动一小段距离,实际上就是前一个点代替后一个点,效果是:曲线上点的位置不变,数量不变,只是这个位置上此点非彼点了。
Q2:曲线点的速度必须取法线方向?
速度的方向其实可以是任意的,但最终只有法线方向的速度才有效,所以一般直接让速度的方向顺着法线。
=====================================================================================
概念二:Curvature Flow / Curvature motion
1. Euclidean geometric heat equation
当取与 Euclidean arc length 有关的导数时,
C
t
C_t
Ct 等于曲线关于弧长的二阶导数


上式表达了曲线
C
C
C 关于时间
t
t
t 的一阶导数等于曲线
C
C
C 关于弧长
s
s
s 的二阶导数
- C s s C_{ss} Css 为曲线关于弧长的二阶导数,基于 Euclidean case
- k k k 为曲线 C C C 的曲率
其显示表示(Explicit form)为:
∂
C
∂
t
=
∂
2
C
∂
S
2
\frac{\partial C}{\partial t} = \frac{\partial ^2C}{\partial S^2}
∂t∂C=∂S2∂2C
Euclidean Case 说明:

Euclidean Transform:
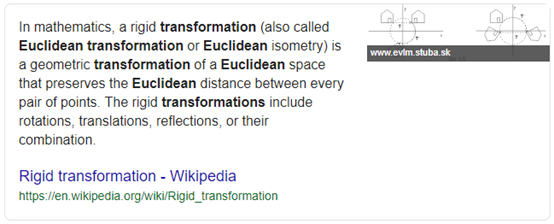
解释一下欧式变换,又称作刚性变换,它能够保持每一对点之间的欧几里得距离。刚性变换包括了旋转、平移、反射或几种变换的组合。
Euclidean Invariant:
意思就是经过 Euclidean transform (rigid transform) 后,两者都根据 motion equation 进行演化,在任意时刻 t t t,两者的形状相同。
Euclidean Case 演化效果:
给出任意一个简单平面曲线(boundary of shape),根据 motion equation(
C
t
=
k
n
C_t = kn
Ct=kn)进行变形,曲线会变得 smooth,成为一个convex;如果继续按照 motion equation 进行变形,convex 又会变得 rounding,不断 vanish 最后成为一个 round circular point。

也就是说,经过 Euclidean Case 的 motion equation 对任意曲线进行变形,都会对曲线施加一个 regular 的效果,首先曲线变得平滑,最后会倾向于坍缩为一个圆点。
2. Affine heat equation
仿射热方程,
C
t
C_t
Ct 的定义如下:

其中 k 就是在 Euclidean case 里的曲线曲率

注意到,这里需要将
C
v
v
C_{vv}
Cvv 先投影到法线方向,而在 Euclidean case 里不需要,是因为 Euclidean transformation 具有 Euclidean invariant,在变换前后点的运动方向也是不变的。而 Affine case 里,不具备 invariant,速度是包括了切线方向分量的。
将 Affine normal 投影到 Euclidean normal,曲率 k k k 变成 1/3 次方。
假设 C v v C_{vv} Cvv 投影到了法线方向,则表达式形式与 Euclidean case 的形式相同: C t = C v v C_t = C_{vv} Ct=Cvv
- C v v C_{vv} Cvv 是曲线的二阶导数,基于Affine arc length
Affine Case 说明:

Affine Transform:
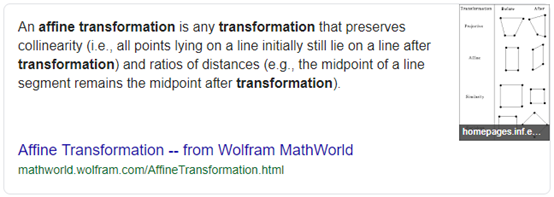
仿射变换是保持共线性的任何变换,变换前属于一条线上的点在变换后仍属于同一条线,且点与点的距离比也保持不变。
和 Euclidean case 类似,经过 Affine transform 后,两者由 motion equation C t = k 1 / 3 n C_t = k^{1/3}n Ct=k1/3n 进行变形,在任意时刻 t,都可以通过一个确定的 transform 将两者联系起来。
Affine Case 演化效果:

和 Euclidean case 一样,首先会进行 smooth,变成一个 convex;
和 Euclidean case 不同的是,其继续演化,会变成一个椭圆的点(lips),而不是圆形点。
3. Constant flow(Constant motion)
顾名思义这种情况下曲线上点的运动是不考虑曲率的,具体做法就是以每个点为圆心,画一个半径相等的圆,下一时刻的点就是圆上的点。
这样做每个点都会走相同的步伐,不管该点处曲率是多少。此时演化出的曲线是平行的,所有点演化前后的距离相等。
Constant motion 特点:
1)offset curves:改变曲线拓扑结构

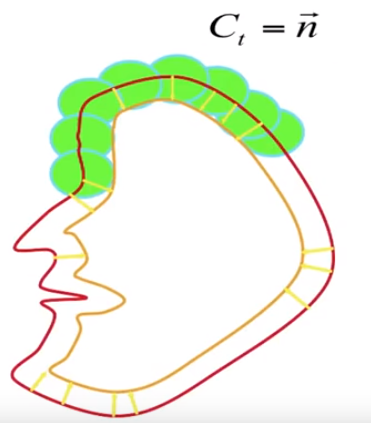
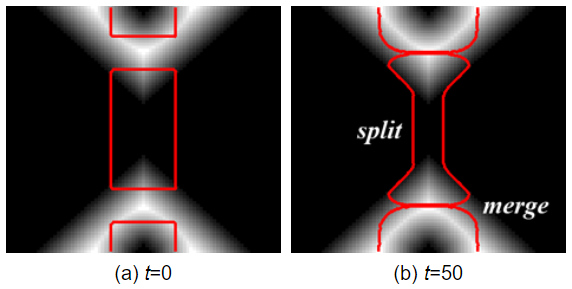
【左图】初始红色的曲线,经过几个时刻的 constant motion,它就有可能改变其拓扑结构,成为两个分离的曲线。而这种 split 不会发生在基于曲率的演化运动中(Euclidean case 或 Affine case)
【右图】初始光滑的红色曲线,经过几个时刻的 constant motion,它会形成 shocks。这是因为 constanct motion 中没有曲率项 k k k,所以它不能理解当曲率非常大的时候,这里就会变成 corner,corner 处的曲率是无线大的,此时曲线的变化速度会非常快,所以就形成了 shocks。同样,这种情况不会发生在基于曲率的演化运动中(Euclidean case 或 Affine case),这两种方式都会让曲线保持光滑,不会形成corner。
总结一下,constant motion 会改变曲线拓扑形状,形成尖角(shocks, corners);Curvature motion 会让曲线变得平滑,我们可以根据不同的任务,将两种 motion 进行结合。

=====================================================================================
概念三:曲线上的计算问题
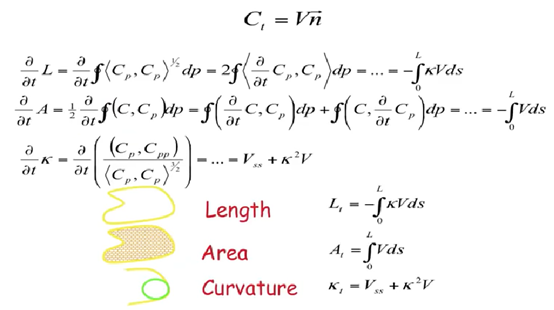
三个表达式分别是 曲线长度随时间的变化,曲线面积随时间的变化,曲线曲率随时间的变化。
“ 不同的 V V V 的取值,决定我们让曲线做什么样儿的 motion ”
1. 当
V
=
1
V = 1
V=1 时,就是 Constant motion

Length:曲率
k
k
k 在整个曲线上的积分恒等于
2
π
2\pi
2π;进一步得知,在
L
(
0
)
2
π
\frac{L(0)}{2\pi}
2πL(0) 时间内,曲线就会坍缩为一个点
Riccati equation:
当时间
t
t
t 和初始时刻曲线的曲率之积恰好等于 1 时,
t
t
t 时刻的曲线曲率就会变成无限大,也就是说,如果满足上面的条件,在经过
t
t
t 个时刻,曲线就会演化为一个 corner,此时 corner 的曲率是无限大的。
另外还能看出,初始时刻的曲线曲率越大,曲线演化出 corner 所需的时间就越少。
总结:在 Constant motion 中,曲线长度以常数 − 2 π -2\pi −2π 进行变化;曲线内部面积的变化与曲线长度 L L L 有关,但它并不是一个常数,因为曲线长度在不停变化,曲线面积是依赖于长度的;曲线的曲率随时间的变化情况等于曲率的平方 k 2 k^2 k2
2. 当 V = k V = k V=k 时,就是 Euclidean motion
此时运动速度与曲线曲率有关

总结:在 Euclidean case 中,曲线内部面积是以常数
−
2
π
-2\pi
−2π 的速度进行减小的(注意和 Constant motion 区分),所以在经过
t
=
A
(
0
)
2
π
t = \frac{A(0)}{2\pi}
t=2πA(0) 个时刻,曲线就会坍缩为一个面积等于 1 的圆
3. 当 V = k 1 / 3 V = k^{1/3} V=k1/3 时,就是 Affine motion
此时运动速度与曲线曲率有关

Affine motion 中没有任何变化为常数。
=====================================================================================
概念四:Activate Contour

前面大括号里的一大堆,都可以看作是
V
V
V
其中, g ( x , y ) g(x,y) g(x,y) 是基于图像的函数,比如它可能和图像的梯度有关
让 g = 1 ∇ T g = \frac{1}{\nabla T} g=∇T1,当图像梯度越大时,g 就越小,相应的导致曲线运动速度 C t C_t Ct 越小,刚好符合我们的需求:当图像梯度很大,说明已经到了边界处,这时我们想要曲线运动速度变小,甚至最后等于0。
简化形式: C t = g k n C_t = gkn Ct=gkn, g g g 为关于图像的函数, k k k 为曲率, n n n 为法线方向上的单位向量
第二项: < ∇ g ( x , y ) , n > <\nabla g(x,y), n> <∇g(x,y),n>
总结:可以自己定义 motion equation,比如:
C t = g k n + n C_t = gkn + n Ct=gkn+n,此时加上的 n 是 constant motion,会让曲线演化更快,但是要小心使用,因为它会产生 shocks;
为了避免 shocks 的产生,也可以让 constanct motion 考虑一下图像特征,定义为 C t = g k n + g n C_t = gkn + gn Ct=gkn+gn
=====================================================================================
概念五:基于曲线演化的图像分割
如果用基于曲线演化的图像分割方法,就是在要分割的图片上,先随便绘制一条曲线,然后让这条曲线演变成我们想要的曲线,分割就完成了。
比如先在目标上随意画一个圈(左图),然后曲线每个点加上运动方向和速度进行演变(中图),最后各点速度都减小到 0,就达到了最终的分割结果(右图)。

要达到上图效果的具体做法:
控制每一个时刻当前曲线上每一个点的运动速度和方向,以一小段曲线举例:
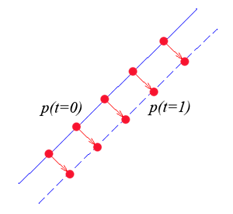
t
=
0
t = 0
t=0 时刻的所有点沿着法线方向演化,在
t
=
1
t = 1
t=1 时刻到达虚线所示的位置,这样就达到了让曲线变化的目的。但这只是最简单的一种情况,如果情况再复杂一点:
1)如果曲线是 V 形的,那么下一时刻点的位置可能无法确定

2)如果曲线在扩张,那么当前时刻的曲线点不足以定义扩张后的曲线,需要插入一些新的点;如果曲线在坍缩,那么又需要移除一些多余的点

3)如果曲线的拓扑结构发生了变化(比如分裂与合并),此时也需要插入或移除一些点
所以结论是:追踪每一个点的运动比较直观,但是实现起来很麻烦,也就是 explicit contours 行不通。
Ⅲ. Snake
Snake 模型优点:
- 将图像数据、初始估计、目标轮廓和基于先验知识的约束统一到一个特征提取的过程中;
- 经过适当地初始化之后,能够自主地收敛于能量极小值状态;
Snake 模型缺点:
- 对初始轮廓敏感,需要依赖其他机制将轮廓放在感兴趣的图像特征附近;
- 有可能收敛到局部极值点,甚至发散;
Snake 模型的可变形曲线: v ( s ) = { x ( s ) , y ( s ) } v(s) = \{x(s), y(s)\} v(s)={x(s),y(s)}
S 为归一化的曲线长度,变化范围 ( 0 , 1 ) (0,1) (0,1)
Snake 模型的总能量函数为:
E
s
n
a
k
e
=
∫
[
E
i
n
t
(
v
(
s
)
)
+
E
e
x
t
(
v
(
s
)
)
]
d
s
E_{snake} = \int [ E_{int}(v(s)) + E_{ext}(v(s)) ]ds
Esnake=∫[Eint(v(s))+Eext(v(s))]ds
- E i n t E_{int} Eint 为内部能量
- E i n t = 1 2 ( α ∣ v ′ ( s ) ∣ 2 + β ∣ v ′ ′ ( s ) ∣ 2 ) E_{int} = \frac{1}{2}(\alpha|v'(s)|^2 + \beta|v''(s)|^2) Eint=21(α∣v′(s)∣2+β∣v′′(s)∣2)
- α \alpha α 和 β \beta β 分别控制模型的弹性和刚性
E e x t E_{ext} Eext 决定吸引轮廓到某种显著的图像特征,这些特征只能根据特定的问题而定义,所以一般外部能量函数不易确定。因此 E e x t E_{ext} Eext 没有统一的数学表达式,必须从问题本身的特性出发,根据实际情况处理。
定义函数
E
e
x
t
=
∫
s
E
i
m
a
g
e
(
v
(
s
)
)
d
s
E_{ext} = \int_s E_{image}(v(s)) ds
Eext=∫sEimage(v(s))ds
其中,
E
i
m
a
g
e
E_{image}
Eimage 如何定义是一个关键问题,典型的做法有:
E
i
m
a
g
e
(
x
,
y
)
=
−
∣
∇
I
(
x
,
y
)
2
∣
E_{image}(x,y) = -|\nabla I(x,y)^2|
Eimage(x,y)=−∣∇I(x,y)2∣
E
i
m
a
g
e
(
x
,
y
)
=
−
∣
∇
(
G
σ
(
x
,
y
)
∗
I
(
x
,
y
)
)
∣
2
E_{image}(x,y) = -|\nabla(G_{\sigma}(x,y) * I(x,y))|^2
Eimage(x,y)=−∣∇(Gσ(x,y)∗I(x,y))∣2
目标轮廓的确定转换成了极小化能量泛函的问题:
E
s
n
a
k
e
=
∫
s
1
2
(
α
(
s
)
∣
v
s
∣
2
+
β
(
s
)
∣
v
s
s
∣
2
)
+
E
i
m
a
g
e
(
v
(
s
)
)
d
s
E_{snake} = \int_s\frac{1}{2}(\alpha(s)|v_s|^2 + \beta(s)|v_{ss}|^2) + E_{image}(v(s))ds
Esnake=∫s21(α(s)∣vs∣2+β(s)∣vss∣2)+Eimage(v(s))ds
由变分法原理出发,将其转换为 Euler 方程:
α
v
s
s
−
β
v
s
s
s
s
−
∇
E
i
m
a
g
e
=
0
\alpha v_{ss} - \beta v_{ssss} - \nabla E_{image} = 0
αvss−βvssss−∇Eimage=0
这一方程可以被看作是轮廓内外力的平衡公式
弹性力:由轮廓的弹性能量产生
F
e
l
a
s
t
i
c
=
α
v
s
s
F_{elastic} = \alpha v_{ss}
Felastic=αvss
特性:弹性力使轮廓连续

刚性力:对应轮廓的刚性能量,也就是曲率
特性:刚性力使轮廓尽可能平滑

外部力:
F
e
x
t
=
−
∇
E
i
m
a
g
e
F_{ext} = -\nabla E_{image}
Fext=−∇Eimage
外部里作用在能使外部能量减小的方向上

离散化
轮廓
v
(
s
)
v(s)
v(s) 由一系列控制点组成,通过依次连接各个控制点并分段线性化得到。
平衡力方程独立作用于各个控制点,能量和平衡力方程均作了离散化处理。
在实际应用中,对 Snake 模型进行离散化后,计算曲线上各个控制点的能量值,能量函数定义:
∑
i
=
1
n
E
i
=
∑
i
=
1
n
(
α
i
E
c
o
n
t
i
n
u
i
t
y
,
i
+
β
i
E
c
u
r
v
a
t
u
r
e
,
i
+
γ
i
E
i
m
a
g
e
,
i
)
\sum_{i=1}^n E_i = \sum_{i=1}^n(\alpha_iE_{continuity,i} + \beta_iE_{curvature,i} + \gamma_iE_{image}, i)
i=1∑nEi=i=1∑n(αiEcontinuity,i+βiEcurvature,i+γiEimage,i)
内部能量的连续性项能量
E
c
o
n
t
i
n
u
i
t
y
,
i
=
∣
d
m
e
a
n
−
∣
v
i
−
v
i
−
1
∣
∣
−
S
m
a
l
l
e
s
t
i
_
c
o
n
t
i
n
u
i
t
y
L
a
r
g
e
s
t
i
_
c
o
n
t
i
n
i
t
y
−
S
m
a
l
l
e
s
t
i
_
c
o
n
t
i
u
i
t
y
E_{continuity,i} = \frac{| d_{mean} - |v_i - v_{i-1}| | - Smallest_{i\_continuity}}{Largest_{i\_continity} - Smallest_{i\_contiuity}}
Econtinuity,i=Largesti_continity−Smallesti_contiuity∣dmean−∣vi−vi−1∣∣−Smallesti_continuity
其中,
∣
d
m
e
a
n
−
∣
v
i
−
v
i
−
1
∣
∣
| d_{mean} - |v_i - v_{i-1}| |
∣dmean−∣vi−vi−1∣∣ 是待考察点的
3
×
3
3 \times 3
3×3 邻域,
d
m
e
a
n
d_{mean}
dmean 表示曲线上相邻点的平均距离,相邻点间的间距和平均值
d
m
e
a
n
d_{mean}
dmean 越接近,其能量值越小,这样即保证了平滑,又避免了堆积
内部能量的曲率项能量
E
c
u
r
v
a
t
u
r
e
,
i
=
1
−
u
i
ω
⋅
u
i
+
1
ω
∣
u
i
ω
∣
⋅
∣
u
i
+
1
ω
∣
−
S
m
a
l
l
e
s
t
i
_
c
u
r
v
a
t
u
r
e
L
a
r
g
e
s
t
i
_
c
u
r
v
a
t
u
r
e
−
S
m
a
l
l
e
s
t
i
_
c
u
r
v
a
t
u
r
e
E_{curvature,i} = \frac{1 - \frac{u^\omega_i \cdot u^\omega_{i+1}}{|u^\omega_i| \cdot |u^ \omega_{i+1}|} - Smallest_{i\_curvature}}{Largest_{i\_curvature} - Smallest_{i\_curvature}}
Ecurvature,i=Largesti_curvature−Smallesti_curvature1−∣uiω∣⋅∣ui+1ω∣uiω⋅ui+1ω−Smallesti_curvature
其中,
C
C
C 是向量
u
i
ω
u_i^\omega
uiω 和
u
i
+
1
ω
u_{i+1}^\omega
ui+1ω 之间的夹角
Δ
θ
\Delta \theta
Δθ 的余弦值,夹角越小,
1
−
C
1-C
1−C 越小,用来估计曲线上各点的曲率
C
=
u
i
ω
⋅
u
i
+
1
ω
∣
u
i
ω
∣
⋅
∣
u
i
+
1
ω
∣
=
(
x
i
−
x
i
−
1
)
(
x
i
+
1
−
x
i
)
+
(
y
i
−
y
i
−
1
)
(
y
i
+
1
−
y
i
)
[
(
x
i
−
x
i
−
1
)
2
+
(
y
i
−
y
i
−
1
)
2
]
[
(
x
i
+
1
−
x
i
)
2
+
(
y
i
+
1
−
y
i
)
2
]
C = \frac{u^\omega_i \cdot u^\omega_{i+1}}{|u^\omega_i| \cdot |u^ \omega_{i+1}|} = \frac{(x_i - x_{i-1})(x_{i+1} - x_i)+(y_i - y_{i-1})(y_{i+1} - y_i)}{\sqrt{[(x_i - x_{i-1})^2 + (y_i - y_{i-1})^2][(x_{i+1} - x_i)^2+(y_{i+1} - y_i)^2]}}
C=∣uiω∣⋅∣ui+1ω∣uiω⋅ui+1ω=[(xi−xi−1)2+(yi−yi−1)2][(xi+1−xi)2+(yi+1−yi)2](xi−xi−1)(xi+1−xi)+(yi−yi−1)(yi+1−yi)
图像能量
表示图像的约束条件,根据有利边界点的原则,边界点应具有较小的值
E
i
m
a
g
e
,
i
=
S
m
a
l
l
e
s
t
i
_
i
m
a
g
e
−
ϕ
e
d
g
e
(
v
i
)
L
a
r
g
e
s
t
i
_
i
m
a
g
e
−
S
m
a
l
l
e
s
t
i
_
i
m
a
g
e
E_{image,i} = \frac{Smallest_{i\_image} - \phi_{edge}(v_i)}{Largest_{i\_image} - Smallest_{i\_image}}
Eimage,i=Largesti_image−Smallesti_imageSmallesti_image−ϕedge(vi)
ϕ
e
d
g
e
(
v
i
)
\phi_{edge}(v_i)
ϕedge(vi) 是边缘检测算子,
L
a
r
g
e
s
t
i
_
i
m
a
g
e
Largest_{i\_image}
Largesti_image 是待考察点的
3
×
3
3 \times 3
3×3 邻域内
ϕ
e
d
g
e
(
v
i
)
\phi_{edge}(v_i)
ϕedge(vi) 的最大值,
S
m
a
l
l
e
s
t
i
_
i
m
a
g
e
Smallest_{i\_image}
Smallesti_image 是最大值,这样的计算用于归一化
在确定能量函数后,对曲线按照能量最小进行迭代。
传统 Snake 方法的不足
1)参数敏感,对初始轮廓要求高
2)搜索范围小
3)容易陷入局部极小值点
4)对于边界上的凹点无法有效跟踪
Snake 模型的改进:
1)改善 Snake 对初始化轮廓的敏感性
2)保证 Snake 能够收敛到全局极值
3)改善 Snake 在能量极小化过程中的收敛速度或数值稳定性
Balloon Force 气球力
在轮廓线上施加另一外部约束力,使轮廓线向目标靠拢。在该力的作用下轮廓线不断地向外膨胀,最终进化到目标轮廓,可以形象的称之为气球力。
气球力所构造的能量项,在能量函数中的数学形式可以表达为:
E
b
a
t
=
m
i
n
n
≤
j
≤
n
,
m
≤
k
≤
m
e
j
k
(
v
i
)
e
i
k
(
v
i
)
=
n
i
⋅
(
v
i
−
p
j
k
(
v
i
)
)
E_{bat} = min_{n \leq j \leq n,m \leq k \leq m} e_{jk}(v_i) e_{ik}(v_i) = n_i \cdot (v_i - p_{jk}(v_i))
Ebat=minn≤j≤n,m≤k≤mejk(vi)eik(vi)=ni⋅(vi−pjk(vi))
其中, p j k ( v i ) p_{jk}(v_i) pjk(vi) 为以控制点 v i v_i vi 为中心的大小为 n × m n \times m n×m 的邻域内的第 ( j , k ) (j,k) (j,k) 个邻点, n i n_i ni 是轮廓线上控制点 v i v_i vi 处的单位法线矢量,这样在规定的邻域内,在法线矢量 n i n_i ni 方向上离控制点 v i v_i vi 最远的点将拥有最小的能量值
引入气球力能量项之后,Snake 模型的外部能量项可以描述为
E
e
x
t
=
E
i
m
a
g
e
+
E
c
o
n
=
k
E
b
a
t
−
l
∣
∇
I
(
v
)
∣
E_{ext} = E_{image} + E_{con} = kE_{bat} - l|\nabla I(v)|
Eext=Eimage+Econ=kEbat−l∣∇I(v)∣
其中参数
k
k
k 用来控制气球力的方向,当
k
k
k 为负数时,气球力使轮廓线向内收缩,反之使轮廓向外膨胀
选择参数 k k k 和 l l l 的大小时,一般将它们置于同一数量集,且 l l l 稍大于 k k k,这是为了在边缘点时轮廓线能够停止运动
这样,原始模型的缺点得到改善,对轮廓线的初始化位置要求明显降低了,即使在初始位置离希望提取的边缘相当远时, Snake 照样能够进化到目标轮廓
该模型改善了 Snake 模型对初始轮廓的敏感性,并且能够跨越图像中的伪边缘点
梯度矢量流 Gradient Vector Flow(GVF)
它的数学基础来源于电磁场理论中的亥姆霍兹理论,这种理论阐明了可以将一种普通的静态矢量场分解为两个组成部分,即无旋场部分和有旋场部分。
在传统的 Active Contour Model 中,图像梯度信息仅仅是作为一个静态的无旋场来平衡方程,但是实际上我们能得到一个更加一般化的静态矢量场,它不仅包含无旋场部分,还包含有旋场部分。
GVF 的提取可以有效地解决曲率变化很大的控制点的收敛效果,但是相对的计算会很慢。
GVF 定义一个力的向量场:
V
(
x
,
y
)
=
(
u
(
x
,
y
)
,
v
(
x
,
y
)
)
V(x,y) = (u(x,y), v(x,y))
V(x,y)=(u(x,y),v(x,y))
GVF Snake 的内外力平衡方程为:
α
v
s
s
−
β
v
s
s
s
s
+
V
=
0
\alpha v_{ss} - \beta v_{ssss} + V = 0
αvss−βvssss+V=0
GVF Snake 定义的能量泛函为:
E
=
∫
∫
μ
(
u
x
2
+
u
y
2
+
v
x
2
+
v
y
2
)
+
∣
∇
f
∣
2
∣
V
−
∇
f
∣
2
d
x
d
y
E = \int\int \mu(u_x^2 + u_y^2 + v_x^2 + v_y^2) + |\nabla f|^2|V - \nabla f|^2 dxdy
E=∫∫μ(ux2+uy2+vx2+vy2)+∣∇f∣2∣V−∇f∣2dxdy
GVF 场可以通过求解下述方程得到:
μ
∇
2
u
−
(
u
−
f
x
)
(
f
x
2
+
f
y
2
)
=
0
μ
∇
2
v
−
(
v
−
f
y
)
(
f
x
2
+
f
y
2
)
=
0
\mu \nabla^2u - (u-f_x)(f_x^2 + f_y^2)=0 \\ \mu \nabla^2v - (v-f_y)(f_x^2 + f_y^2)=0
μ∇2u−(u−fx)(fx2+fy2)=0μ∇2v−(v−fy)(fx2+fy2)=0
∇
2
\nabla ^2
∇2 是拉普拉斯算子
上述方程的求解是通过顺序迭代 u u u 和 v v v 实现的
GVF 能够检测到边界上凹点的原因:
使得
∇
f
\nabla f
∇f 由
∣
∇
f
∣
|\nabla f|
∣∇f∣ 大的地方向
∣
∇
f
∣
|\nabla f|
∣∇f∣ 小的地方扩散,因而扩大了 Snake 模型的捕捉范围,也能较好地进入深度凹陷区域
GVF 和 传统 Snake 比较:
传统 Snake Force:

GVF Force:


内外力示意图:

实验结果对比:
左图为传统 Snake,右图为 GVF

经过动态参数修正后得到最终的轮廓线:

选取的初始轮廓甚至可以与目标轮廓相交,而传统 Snake 方法是无法实现的
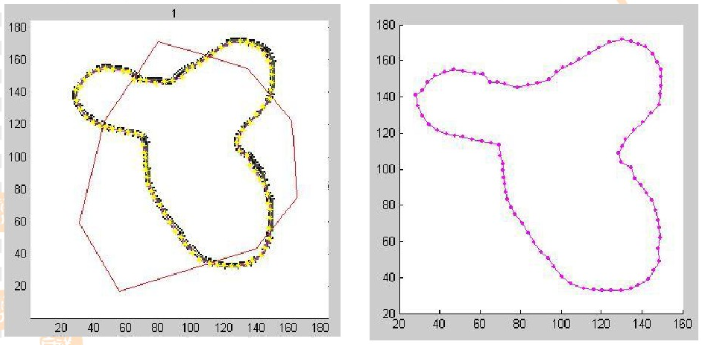
GVF Snake 的缺点:
1)参数敏感
2)计算代价高,速度慢
3)初始轮廓的选取有临界点
其他改进方法:
1.B-Snake 模型
目标轮廓使用 B- 样条来表达,利用参数 B 样条的局部控制能力及参数连续性等特点,改进了原模型中存在的一些缺陷,例如不稳定的数据特性、收敛速度慢、很难处理不连贯性、对噪声的敏感性。
2.双主动轮廓模型
在所需要提取的目标轮廓内部和外部各放置一个主动轮廓线,分别为内轮廓线和外轮廓线。
在初始情况下,两个轮廓线独立进行,分别向目标轮廓收敛,互不影响;当两个轮廓线都静止不动时,则分别对内外轮廓进行能量计算并比较,选择能量较大的一个轮廓线,对其施加一个外部作用力,该力的方向指向另外一个轮廓线,强制使当前轮廓线从当前平衡位置离开,然后重新启动演化进程,当达到平衡时,再次进行能量比较并重复以上步骤,直至最终内外轮廓线的能量之差减小到允许的范围。
优点:可以有效解决由于被噪声所引起的奇异点吸引而陷入能量局部最小的问题
Ⅳ. Level Set
Level Set Method 是一种进化版的 Snake 算法,也是需要给定初始的轮廓曲线,然后根据泛函能量最小化来演化曲线。但水平集的方法用的是一种隐函数的方法。
=====================================================================================
概念一:曲线的隐式和显式表达
1. Explicit representation 曲线的显式表示
平面曲线直观上可以用每个点的位置来表示

2. Implicit representation 曲线的隐式表示
一个闭合的平面曲线:
C
(
p
)
:
R
1
→
R
2
C(p): R^1 → R^2
C(p):R1→R2,从几何上,这条曲线可以被隐式地表示为:
C
=
{
(
x
,
y
)
∣
ϕ
(
x
,
y
)
=
0
}
C = \{(x,y) | \phi(x,y) = 0 \}
C={(x,y)∣ϕ(x,y)=0}
此时曲线上的点,能够使函数 ϕ = 0 \phi = 0 ϕ=0,所以我们的目标就是找到这样一个函数 ϕ \phi ϕ,当 ( x , y ) ∈ C (x,y) \in C (x,y)∈C 时, ϕ = 0 \phi = 0 ϕ=0,否则 ϕ ≠ 0 \phi ≠ 0 ϕ=0。
=====================================================================================
概念二:什么是 Level Set
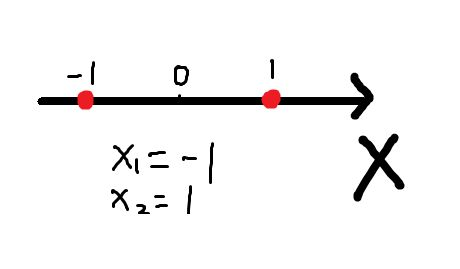
先看 一维 的情况:要描述直线上的两个点,可以直接写出两个点的坐标:
x
1
=
−
1
x_1 = -1
x1=−1 和
x
2
=
1
x_2 = 1
x2=1
也可以用集合的形式表示:
{
x
∣
f
(
x
)
=
x
2
=
1
}
\{x|f(x) = x^2 = 1\}
{x∣f(x)=x2=1},此时
x
x
x 的取值就为集合
{
−
1
,
1
}
\{-1, 1\}
{−1,1}

实际上这里
y
y
y 的取值就是 Level,可以表达成:Level 为 1 的所有
x
x
x 取值的集合。
再看 二维 的情况:对于曲线来说,可以直接用一个参数方程表示一条曲线:
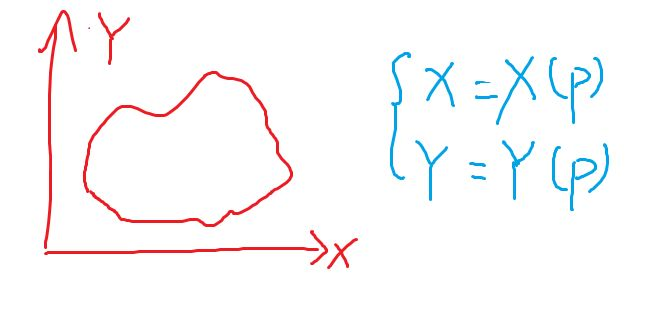
或者也用集合的表示形式:
{
(
x
,
y
)
∣
z
=
f
(
x
,
y
)
=
l
}
\{(x,y)|z = f(x,y) = l\}
{(x,y)∣z=f(x,y)=l},表达成曲面在 Level
l
l
l 下的所有点
(
x
,
y
)
(x,y)
(x,y) 的集合,一般会选择 Level = 0,也就是
f
(
x
,
y
)
=
0
f(x,y) = 0
f(x,y)=0,对应下图中红色曲线,曲线上的点均满足
f
(
x
,
y
)
=
0
f(x,y) = 0
f(x,y)=0

小结:Level Set 实际就是 “满足某一条件的所有点的集合”,这个概念其实很像数学中的隐函数,不直接表达
x
x
x 和
y
y
y 的关系是什么,而是通过一个函数将这两者联系起来。圆的方程就是一个很好的例子:
x
2
+
y
2
=
1
x^2 + y^2 = 1
x2+y2=1
而它本来的显式表达应该是:
y
=
+
1
−
x
2
y
=
−
1
−
x
2
y = + \sqrt{1 - x^2} \\ y = - \sqrt{1 - x^2}
y=+1−x2y=−1−x2
=====================================================================================
概念三:用 Level Set Method 实现曲线演化
我们的目的是为了描述一条平面曲线的变化情况,但是问题在于一条曲线在运动过程中可能会分裂成好几条曲线,或者几条曲线在运动过程中合并成一条曲线,这样的拓扑变化不可能用一条连续的参数化曲线来表示,因为连续参数化曲线是用一个一元函数表示的,它显然不可能表示多条分开的曲线,这和连续性相矛盾。
换一个角度,我们可以用一个连续变化的曲面和固定水平面的交线来表示曲线,这个曲面本身不发生拓扑变化,它始终是一个固定的连续二元函数 z = f ( x , y ) z = f(x,y) z=f(x,y),只需要通过上下移动曲面来改变曲面和水平面的交线,就能达到改变曲线的目的。
这种思想就是 Level Set Method,就是用更高一维的函数去解决当下的问题,比如上面说过的:用二维线表示一维点,用三维面表示二维线。

所以,想要研究曲线
C
:
y
=
f
(
x
)
C: y = f(x)
C:y=f(x),可以先升一维表示成
Z
=
f
(
x
,
y
)
=
0
Z = f(x,y) = 0
Z=f(x,y)=0,此时虽然有三个变量
x
x
x,
y
y
y,
z
z
z,但提取一个变量
Z
Z
Z 用另外两个变量表示时,就相当于降低了一维,从三维曲面下降到了二维曲线。
于是,我们想要做的曲线演变,就可以转化成 Z = f ( x , y ) Z = f(x,y) Z=f(x,y) 随时间的演变。
小结: 平面曲线可以表示成一个二元函数 z = f ( x , y ) z = f(x,y) z=f(x,y) 的零点集合(Zero Level Set),即这个二元函数所表示的三维曲面与 X Y XY XY 平面的交线。更一般地,任何 N N N 维曲面都可以表示为一个 N + 1 N+1 N+1 维曲面与一个 N N N 维超平面的交集,或称 N + 1 N+1 N+1 维曲面在一个 N N N 维超平面上的投影。通过 Level Set Method,就可以用曲面 ϕ \phi ϕ 隐式地处理曲线 C C C。
问题一:Level 为什么要取 0?
取一个固定的值是为了将函数的第 3 维固定住,好让函数从 3 维降到 2 维。至于为什么要固定在 Level 0 而不是 1 或 2 或 3 …,应该是取 0 表示最简单,不会有多余的常数项。
另外要注意,在演化时,水平面 Z = 0 Z = 0 Z=0 并没有改变,即切面不变,变的是 3 维曲面,即 ϕ \phi ϕ 在上上下下地移动。
问题二:曲面 ϕ \phi ϕ 取值的正负问题
我们可以定义水平集函数(曲面)
ϕ
\phi
ϕ 在曲线内部取正值,在曲线外部取负值。

可以想象三维空间中的一个曲面
ϕ
\phi
ϕ,当
Z
=
0
Z=0
Z=0 时,就刚好对应了平面
X
Y
XY
XY,此时平面
X
Y
XY
XY 和曲面
ϕ
\phi
ϕ 的交叉处,就是我们的曲线
C
C
C,此时我们可以称之为:曲面
ϕ
\phi
ϕ 的 Level 等于 0 时所对应的曲线。
直观的看,下图黑色直线表示水平线,左边的小红鸭是俯视图,红色部分(曲线内部)高于水平线,白色部分(曲线外部)低于水平线,其轮廓上的点恰好在水平线上;右边是小红鸭从底部看的侧视图,补充说明了哪些部分高于/低于水平线。

也就是说,曲线内部都会在水平轴上方,曲线外部都会在水平轴下方,而曲线上的点恰好是
ϕ
=
0
\phi = 0
ϕ=0 的点。
问题三:点到曲线的距离
有了曲面 ϕ \phi ϕ 取值的正负概念,就很容易理解点到曲线的正负性:
- 曲线上所有的点,到曲线的距离都是 0,这个很好理解;
- 曲线内部的点,到曲线的距离为负,可以理解为曲面 ϕ \phi ϕ 在曲线内部取正值,即比水平面高,到水平面需要“下降”;
- 曲线外部的点,到曲线的距离为正,可以理解为曲面 ϕ \phi ϕ 在曲线外部取负值,即比水平面低,到水平面需要“上升”;
问题四:为什么要用 Level Set 表示曲线
在 Level Set Method 之前,有个 Snake 方法,它也是基于能量泛函的方法。其核心思想是,首先在感兴趣区域的附近给出一条初始曲线,接下来在曲线固有内力(控制曲线的弯曲和拉伸)和图像外力(控制收敛到局部特征)的作用下收敛到目标的边界轮廓。但是 Snake 方法存在的问题就是:需要将曲线进行参数化,而且还不善于处理曲线的拓扑变换。
1. Level Set Method 可以实现复杂的拓扑结构变化,比如在演化前是相邻的点,演化后非相邻点,用直接处理曲线的方式很难实现

2. 函数
ϕ
\phi
ϕ 会随着梯度(速度)进行移动,可以直接基于 Level 对曲线进行处理,而不需要考虑曲线的碰撞和移动
最后的效果就是,当曲面在演变时,截面曲线也会跟着扩张、坍缩或者消失。(a)、(b) 显示了曲线合并过程,(c)、(d) 显示了曲线分裂过程。
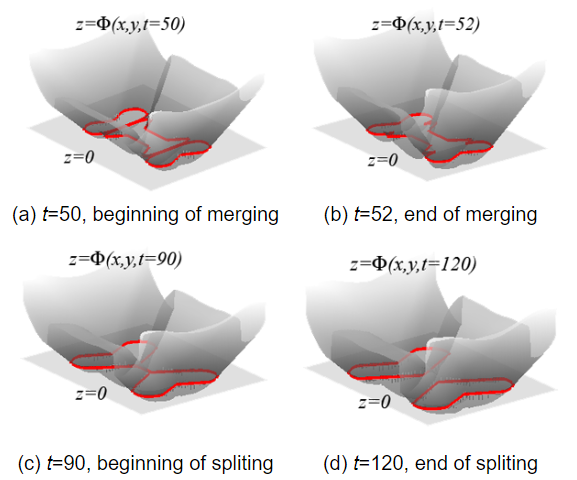
用曲面的运动实现曲线的演化,就不需要额外考虑插入、移除曲线点,也不需要考虑拓扑结构的变化。
Level Set Method 的基本思想是将平面闭合曲线隐式地表达为二维曲面函数的水平集,即具有相同函数值的点集,通过 Level Set 函数曲面的进化隐式地求解曲线的运动。尽管这种转化使得问题在形式上变得复杂,但在问题的求解上带来很多优点,其最大的优点在于曲线的拓扑变化能够得到很自然的处理,而且可以获得唯一的满足熵条件的弱解。
问题五:如何用三维控制二维
让三维曲面控制二维曲线:
- 控制曲线的演变速度:用曲面的梯度信息
- 控制曲线的演变方向:用最优方向,即法线方向
=====================================================================================
概念四:用 Level Set 表示曲线
想要用 Level Set 表示平面曲线 C C C,需要计算 切线方向、法线方向、曲率。
1. Level Set Normal & Tangential (法向 & 切向)

设:平面曲线的法线方向为
N
N
N,切线方向为
T
T
T(和法线方向垂直),另外,
∇
ϕ
\nabla \phi
∇ϕ 为水平集函数
ϕ
\phi
ϕ 的梯度。
定义:法线(切线)方向向量分别为:

说明:
- 曲线的梯度方向和法线方向相同
- N 和 T 是 整个 平面曲线的法线方向和切线方向
- 法向向量取负是因为这里取内法线方向
证明法线方向向量:
首先要明确,在 ϕ \phi ϕ 的 level 固定时,沿着当前 level 的曲线走一圈, ϕ \phi ϕ 的值不会变化。
导数是衡量 “变化“ 的量,那么既然沿着曲线走一圈, ϕ \phi ϕ 的值不会变化,则 ϕ \phi ϕ 对曲线弧长的导数自然等于 0,即 ϕ s = 0 \phi_s = 0 ϕs=0,其中 s s s 为曲线弧长。
假设这里取 Level = 0,则所有属于曲线上的点都会使得: ϕ = 0 \phi = 0 ϕ=0
根据链式法则知:
ϕ x x s + ϕ y y s \phi_xx_s + \phi_yy_s ϕxxs+ϕyys 可以看作一个内积的形式,即向量 ( ϕ x , ϕ y ) (\phi_x, \phi_y) (ϕx,ϕy) 和 ( x s , y s ) (x_s, y_s) (xs,ys) 的内积;而 ϕ \phi ϕ 的梯度 ∇ ϕ = ( ϕ x , ϕ y ) \nabla \phi = (\phi_x, \phi_y) ∇ϕ=(ϕx,ϕy),切线方向向量 T = ( x s , y s ) T = (x_s, y_s) T=(xs,ys),所以这里就将其看作是 ∇ ϕ \nabla\phi ∇ϕ 与 T T T 的内积。
- 向量 a = ( a 1 , a 2 ) a=(a1, a2) a=(a1,a2) 和 b = ( b 1 , b 2 ) b=(b1, b2) b=(b1,b2) 的内积等于 a 1 × b 1 + a 2 × b 2 a1 \times b1 + a2 \times b2 a1×b1+a2×b2
- x s x_s xs 和 y s y_s ys 是单位向量, ϕ x \phi_x ϕx 和 ϕ y \phi_y ϕy 分别是关于 x x x 和 y y y 方向的梯度
由上面两个式子可知:
对 ∇ ϕ \nabla \phi ∇ϕ 进行正则化,使其变成单位向量,这里内积仍然等于0,因为正则化只是改变了向量大小而不改变方向。
- 内积为 0 的两个向量互相垂直
- 法线方向向量取负是因为这里设定它的方向是朝向曲线内部
2. Level Set Curvature 曲率

曲率是平面曲线关于弧长的二阶导数,即
C
s
s
=
k
n
C_{ss} = kn
Css=kn,其中
k
k
k 为曲率,
n
n
n 为单位向量。
定义:曲率计算公式

d
i
v
(
α
,
β
)
=
α
x
+
β
y
div(\alpha, \beta) = \alpha_x + \beta_y
div(α,β)=αx+βy,它是一个标量。即:向量的第一个 term
α
\alpha
α 对坐标轴 x 求导,向量的第二个 term
β
\beta
β 对坐标轴 y 求导
证明曲率等式:
由于在同一 Level Set 下,曲线 ϕ \phi ϕ 的值相同,这里仍假设取 Level = 0,即 ϕ = 0 \phi = 0 ϕ=0,所以 ϕ \phi ϕ 关于弧长 s s s 的一阶导和二阶导均为 0: ϕ s = 0 \phi_s = 0 ϕs=0, ϕ s s = 0 \phi_{ss} = 0 ϕss=0
ϕ \phi ϕ 沿着曲线关于弧长的二阶导数 ϕ s s ( x , y ) \phi_{ss}(x,y) ϕss(x,y) 计算如下:
- 对内积 d d s < ∇ ϕ , T > \frac{d}{ds}<\nabla \phi, T> dsd<∇ϕ,T> 求导等于第一项的导数与第二项的内积 + 第一项与第二项导数的内积
又已知 ϕ s s = 0 \phi_{ss} = 0 ϕss=0,所以:
对于上式的第一项,可以改写为:
第一个证明里已经提过,根据链式法则有 ϕ \phi ϕ 关于弧长 s s s 的一阶导: ∇ ϕ = ϕ x x s + ϕ y y s \nabla \phi = \phi_xx_s + \phi_yy_s ∇ϕ=ϕxxs+ϕyys,这里 ∇ ϕ \nabla \phi ∇ϕ 再次对 s s s 求导: d d s ∇ ϕ = d d s ( ϕ x x s + ϕ y y s ) = \frac{d}{ds}\nabla \phi = \frac{d}{ds}(\phi_xx_s + \phi_yy_s) = dsd∇ϕ=dsd(ϕxxs+ϕyys)=对于上式的第二项,由于 k k k 是标量,所以可以直接提到内积运算符外面来,得到下面一行式子:
由于两项之和为0,所以有:
通过对上式变形和化简,就能得到曲率 k = d i v ( ∇ ϕ ∣ ∇ ϕ ∣ ) k = div(\frac{\nabla \phi}{|\nabla \phi|}) k=div(∣∇ϕ∣∇ϕ)。
所以我不需要明确地知道曲线 C C C 是什么,我只需要隐式地表达出 C C C 即可,这样一来计算曲率、法线、切线向量时,不需要追踪曲线本身每个点如何如何,而是基于 Level 来进行计算,也可以说成基于 image 进行计算,这样就简单的多了。
=====================================================================================
概念五:如何演化水平集函数(曲面) ϕ \phi ϕ
曲线
C
C
C 是曲面 Level 等于 0 时的隐式表达:

曲线速度为
d
C
d
t
\frac{dC}{dt}
dtdC,曲面
ϕ
\phi
ϕ 的速度为
d
ϕ
d
t
\frac{d\phi}{dt}
dtdϕ:

证明曲面
ϕ
\phi
ϕ 的速度为
V
∣
∇
ϕ
∣
V|\nabla \phi|
V∣∇ϕ∣:
取曲线 C = { ( x , y ) : ϕ ( x , y ) = 0 } C = \{(x,y): \phi(x,y) = 0\} C={(x,y):ϕ(x,y)=0},此时 ϕ \phi ϕ 的值恒为 0,所以 ϕ \phi ϕ 对 t t t 的导数也为 0。
根据链式法则有:
将上式变形一下,得到:
将 ϕ x x t + ϕ y y t \phi_xx_t + \phi_yy_t ϕxxt+ϕyyt 写成内积的形式,上面已经写过 C t = V N C_t = VN Ct=VN,其中 V V V 是一个标量,可以直接从内积运算中提出。将法线方向向量带入内积运算中,最后可以得到 ϕ t \phi_t ϕt 的结果:
=====================================================================================
概念六:速度函数 ϕ \phi ϕ
零水平集以速度 V V V 沿着其法线方向运动,运动方程可以表示为 ϕ t = V ∣ ∇ ϕ ∣ \phi_t = V|\nabla \phi| ϕt=V∣∇ϕ∣
Level Set Method 进行边界轮廓提取的关键是 根据实际问题的需要选取合适的速度函数
F
F
F,
F
F
F 一般是与图像相关的项(梯度信息)以及与轮廓曲线的几何形状有关的项(曲率)的函数。

其中,
F
F
F 表示曲线上各点的演化速度,方向沿着曲线的法线方向,
F
F
F 通常与图像梯度和曲线曲率有关。
=====================================================================================
概念七:水平集函数 ϕ \phi ϕ 的确定
曲线上的点用
x
=
(
x
,
y
)
x = (x,y)
x=(x,y) 表示,在经过
t
t
t 个时刻的演化后,得到新的点
x
t
x_t
xt,那么在任意时刻
t
t
t,曲线上的点
x
(
t
)
x(t)
x(t) 可以由曲面上高度为 0 的点的集合来表示:
ϕ
(
x
(
t
)
,
t
)
=
0
\phi(x(t), t) = 0
ϕ(x(t),t)=0
但是这样仍然不知道曲面方程 ϕ ( x ( t ) , t ) \phi(x(t),t) ϕ(x(t),t) 是什么,因为只要 Level 等于 0 时能给我们目标 contour 的所有曲面方程都可以。
定义:表面高度等于
(
x
,
y
)
(x,y)
(x,y) 点到目标 contour 上最近一个点的距离:
ϕ
(
x
,
y
,
t
=
0
)
=
±
d
\phi(x,y,t=0) = \pm d
ϕ(x,y,t=0)=±d
- 当 d d d 为正时,就表示 Level 为 + d +d +d 的一条曲线,且该曲线是原曲线扩张得到的,其在 Level 0 曲线的外部
- 当 d d d 为负时,就表示 Level 为 − d -d −d 的一条曲线,且该曲线是原曲线坍缩得到的,其在 Level 0 曲线的内部
- 所以,初始的水平集函数 ϕ \phi ϕ 可以是任意的,只要它的 Zero Level Set 表示了初始的 contour 即可
给定一个 t = 0 t = 0 t=0 时的初始曲线 ϕ \phi ϕ,根据 运动方程 ∂ ϕ ∂ t \frac{\partial \phi}{\partial t} ∂t∂ϕ 就可以知道任意时刻 t t t 的曲线表达式。并且当运动方程 ∂ ϕ ∂ t = 0 \frac{\partial \phi}{\partial t} = 0 ∂t∂ϕ=0 时,就可以认为此时曲线 ϕ \phi ϕ 不再变化。
根据链式法则,运动方程
∂
ϕ
∂
t
=
0
\frac{\partial \phi}{\partial t} = 0
∂t∂ϕ=0 可以写为:

- x t x_t xt、 ϕ t \phi_t ϕt 的下标 t t t 表示对 t t t 求导
- 曲线在某一个点 x x x 处的梯度为 ∂ ϕ ∂ x = ∇ ϕ \frac{\partial \phi}{\partial x} = \nabla \phi ∂x∂ϕ=∇ϕ
- x x x 点的速度 x t x_t xt 由法线方向的力 F F F 决定,即 x t = F ( x ( t ) ) n x_t = F(x(t))n xt=F(x(t))n,其中 n = ∇ ϕ ∣ ∇ ϕ ∣ n = \frac{\nabla \phi}{|\nabla \phi|} n=∣∇ϕ∣∇ϕ 是法线方向的单位向量
- 曲面上每一个点的运动速度 ϕ t = V N \phi_t = VN ϕt=VN,其中 V 是速度大小,N 是曲线的法线方向
上面的运动方程可以继续变形为:

最后一个等式就定义了曲线
ϕ
\phi
ϕ 的运动,可以计算任意
t
t
t 时刻曲面
ϕ
t
\phi_t
ϕt,同时也就知道了
ϕ
\phi
ϕ 的表达式。
另外,知道曲面
ϕ
\phi
ϕ 的表示时,自然就可以得到其表面曲率
k
k
k:

曲率
k
k
k 可以控制曲线的平滑度。
=====================================================================================
概念八:图像的梯度计算
图像在计算机中是以数字图像的形式进行存储的,所以图像其实是 离散 的数字信号,那么计算图像的梯度就不能用连续函数计算微分的方式,而是用差分来代替连续信号中的微分。
差分通常考虑三种形式:正向、反向和中心差分
1)正向差分:

2)反向差分:

3)中心差分:

计算图像梯度:
d
x
(
i
,
j
)
=
I
(
i
+
1
,
j
)
−
I
(
i
,
j
)
d
y
(
i
,
j
)
=
I
(
i
,
j
+
1
)
−
I
(
i
,
j
)
dx(i,j) = I(i+1,j) - I(i,j) \\ dy(i,j) = I(i,j+1) - I(i,j)
dx(i,j)=I(i+1,j)−I(i,j)dy(i,j)=I(i,j+1)−I(i,j)
其中, I I I 是图像当前像素的值(比如 RGB 值)
由于中心差分误差更小,所以计算图像梯度一般会用中心差分:
d
x
(
i
,
j
)
=
I
(
i
+
1
,
j
)
−
I
(
i
−
1
,
j
)
2
d
y
(
i
,
j
)
=
I
(
i
,
j
+
1
)
−
I
(
i
,
j
−
1
)
2
dx(i,j) = \frac{I(i+1,j) - I(i-1,j)}{2} \\ dy(i,j) = \frac{I(i,j+1) - I(i,j-1)}{2}
dx(i,j)=2I(i+1,j)−I(i−1,j)dy(i,j)=2I(i,j+1)−I(i,j−1)
=====================================================================================
概念:Level Set 能量函数的构造
先看不是 Level Set 方法时,能量函数的构造:
假设:黑色区域为分割目标,白色轮廓为当前的曲线 C

基于图像特征的 外部能量 可以定义为:
E
e
x
t
=
E
1
+
E
2
=
∫
i
n
s
i
d
e
(
C
)
∣
u
0
(
x
,
y
)
−
c
1
∣
2
d
x
d
y
+
∫
o
u
t
s
i
d
e
(
C
)
∣
u
0
(
x
,
y
)
−
c
2
∣
2
d
x
d
y
E_{ext} = E_1 + E_2= \int_{inside(C)}|u_0(x,y) - c_1|^2dxdy + \int_{outside(C)}|u_0(x,y)-c_2|^2dxdy
Eext=E1+E2=∫inside(C)∣u0(x,y)−c1∣2dxdy+∫outside(C)∣u0(x,y)−c2∣2dxdy
其中
c
1
c_1
c1,
c
2
c_2
c2 分别是轮廓曲线
C
C
C 内部和外部所有像素点像素值的平均,
u
0
(
x
,
y
)
u_0(x,y)
u0(x,y) 为图像上像素
(
x
,
y
)
(x,y)
(x,y) 处的像素值。
(1)
E
1
>
0
E_1 > 0
E1>0,
E
2
≈
0
E_2 ≈ 0
E2≈0,
E
e
x
t
>
0
E_{ext} > 0
Eext>0
(2)
E
1
≈
0
E_1 ≈ 0
E1≈0,
E
2
>
0
E_2 > 0
E2>0,
E
e
x
t
>
0
E_{ext} > 0
Eext>0

(3)
E
1
>
0
E_1 > 0
E1>0,
E
2
>
0
E_2 > 0
E2>0,
E
e
x
t
>
0
E_{ext} > 0
Eext>0
(4)
E
1
≈
0
E_1 ≈ 0
E1≈0,
E
2
≈
0
E_2 ≈ 0
E2≈0,
E
e
x
t
≈
0
E_{ext} ≈ 0
Eext≈0

以上四种情况,只有曲线轮廓和目标轮廓重合时,总能量才达到最小,其余情况能量均大于 0
内部能量通常是一些正则化项,包括规范曲线的长度等,所以总能量函数可以表示为:
E
=
μ
L
e
n
g
t
h
(
C
)
+
λ
1
E
1
+
λ
2
E
2
E = \mu Length(C) + \lambda_1 E_1 + \lambda_2E_2
E=μLength(C)+λ1E1+λ2E2
在 Level Set 方法中,如果按上面的思路做,就需要确定曲线的内部和外部。
在二维平面上,曲线方程及曲线的内、外部可以表示为:

将二维曲线放入三维空间中,曲线方程及曲线的内、外部可以表示为:

α \alpha α β \beta β
=====================================================================================
概念九:Level Set Method 在计算机中的具体实现
在计算机中,图像是由一个一个的像素表示的,所以上面的函数就需要离散化,也就是曲面运动速度
ϕ
t
\phi_t
ϕt 需要在每个像素点
(
i
,
j
)
(i,j)
(i,j) 上进行离散化的计算:
ϕ
(
i
,
j
,
t
+
Δ
t
)
−
ϕ
(
i
,
j
,
t
)
Δ
t
\frac{\phi (i, j, t+ \Delta t) - \phi(i,j,t)}{\Delta t}
Δtϕ(i,j,t+Δt)−ϕ(i,j,t)
连续函数算微分,离散函数算差分,其实目的是一样的。那么现在像素点
(
i
,
j
)
(i,j)
(i,j) 处的梯度就通过有限差分的形式计算:

其中,
∇
+
x
(
i
,
j
)
\nabla^{+x}(i,j)
∇+x(i,j) 和
∇
−
x
(
i
,
j
)
\nabla^{-x}(i,j)
∇−x(i,j) 分别是像素
(
i
,
j
)
(i,j)
(i,j) 前向和后向的梯度。
- F > 0 F > 0 F>0 代表力沿着法线方向向外
- F < 0 F < 0 F<0 代表力沿着法线方向向内
-
Δ
−
x
ϕ
\Delta^{-x}\phi
Δ−xϕ 和
Δ
+
x
ϕ
\Delta^{+x}\phi
Δ+xϕ 分别是给定像素点后向和前向的有限差分。

梯度的计算与向前运动的方向有关( F F F的方向),而有限差分的计算方式刚好能考虑到这一点。
刚才推出来的运动公式(motion equation):
ϕ
t
+
F
∣
∇
ϕ
∣
=
0
\phi_t + F|\nabla \phi| = 0
ϕt+F∣∇ϕ∣=0
此时就可以变形为:
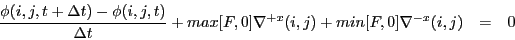
其中,曲线速度
ϕ
t
\phi_t
ϕt 表达为了前向差分的形式,后面两项相当于根据
F
F
F 的值进行选择计算,当
F
>
0
F > 0
F>0 时计算第二项,第三项刚好为 0,同理可知
F
<
0
F < 0
F<0 的运算情形。
所以,曲面
ϕ
(
i
,
j
)
\phi(i,j)
ϕ(i,j) 的更新公式就可以由上式变形而来,因为我们的目的是求下一时刻曲面是什么,即
ϕ
(
i
,
j
,
t
+
Δ
t
)
\phi(i,j,t+\Delta t)
ϕ(i,j,t+Δt),所以只要进行相应的变形,就能得到:

同样,只要有了曲线
ϕ
\phi
ϕ 的表达式,就可以根据中心差分计算出曲率,首先计算:

得曲率
k
k
k 为:

为了保持前向的平滑性,高曲率的部分应该给予惩罚。也就是说,在曲率比较大时,我们的措施不是让曲面
ϕ
\phi
ϕ 向下移动来扩大 Zero Level Set 从而降低曲率,而是通过这个高曲率改变运动方式,也就是要根据高曲率来更新曲面方程
ϕ
(
i
,
j
)
\phi(i,j)
ϕ(i,j):
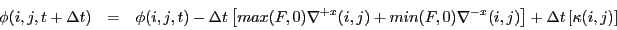

初始轮廓会在目标轮廓内部上扩张(
F
>
0
F > 0
F>0),在目标轮廓外部坍缩(
F
<
0
F < 0
F<0)
=====================================================================================
总结 Level Set Method:
我们的目的是要实现 曲线 的演变,即 ∂ C ∂ t = V N \frac{\partial C}{\partial t} = VN ∂t∂C=VN,但困难在于无法参数化曲线 C C C,所以提出用 Level Set 隐式地表示曲线,将 Level 固定在 0,所以有曲线的隐式表达式: { ( x , y ) ∣ ϕ ( x , y ) = 0 } \{(x,y) | \phi(x,y) = 0\} {(x,y)∣ϕ(x,y)=0}
而水平集函数(曲面) ϕ \phi ϕ,只要按照它的 motion equation ∂ ϕ ∂ t = V ∣ ∇ ϕ ∣ \frac{\partial \phi}{\partial t} = V|\nabla \phi| ∂t∂ϕ=V∣∇ϕ∣ 去演变,那么在任意时刻 t t t,其 Zero Level Set 表示的曲线总是我们想要的曲线。
实现曲面的演变也很简单,初始时刻我们随便选取一个曲面,只要它的 Zero Level Set 为初始曲线即可,然后根据 V V V 和当前曲面的梯度,就能得到曲面的变化 ∂ ϕ ∂ t \frac{\partial \phi}{\partial t} ∂t∂ϕ,然后对曲面 ϕ \phi ϕ 加上这个变化即可 ϕ = ϕ + Δ ϕ \phi = \phi + \Delta \phi ϕ=ϕ+Δϕ
我们一般说的函数是关于变量的,而泛函通俗讲就是关于函数的函数,Level Set Method 构建的能量泛函就是关于水平集函数 ϕ \phi ϕ 的函数。当极小化这个泛函时,水平集函数 ϕ \phi ϕ 的零水平集也就收缩到目标边界轮廓上。这是因为零水平集受到内力和外力作用,当和目标重合时,内外力平衡,能量极小化。
水平集常用在活动轮廓 active contour 方法中表示曲线,而活动轮廓又分为基于区域的和基于边缘的方法。
安利一个大牛,李纯明,现在回国了,之前就是看他的水平集文章,有两篇都是best paper。其中基于区域的方法可以看李纯明教授的RSF,写的很好,不依赖于初始化,还有相关代码也公开了。基于边缘的方法可以看他的DRLSE,对初始化敏感,但是对简单图效果很好。这两篇看完如果还很迷糊,当然我也迷糊。。。你可以再去看看蛇模型和CV,看看区别,总结一下,感觉就可以了,有些东西说是说不粗来的。
,水平集应该说是主动轮廓方法(Active Contour Model,ACM)的一种具体解法
学习路线:
【1】《Distance Regularized Level Set Evolution and Its
Application to Image Segmentation》Chunming Li,
code:DRLSE,DRLSE(MatLab)
【2】《A Locally Statistical Active Contour Model for Image Segmentation with Intensity Inhomogeneity》 Kaihua Zhang, Lei Zhang etc, 2013
主页:LSACM
论文:https://arxiv.org/abs/1305.7053
code:LSACM
【3】《A Level Set Approach to Image Segmentation With Intensity Inhomogeneity》 Kaihua Zhang, Lei Zhang etc, 2017
论文:LSISII
【4】《Active contours with selective local or global segmentation: A new formulation and level set method》 K. Zhang, L. Zhang, H. Song and W. Zhou, 2010
主页:VIC_webpage
论文:VIC.pdf
code:IVC.zip
【5】《Active contours driven by local image fitting energy》 K. Zhang, H. Song, and L. Zhang,PR 2010
【6】《A VARIATIONAL MULTIPHASE LEVEL SET APPROACH TO SIMULTANEOUS SEGMENTATION AND BIAS CORRECTION》K. Zhang, L. Zhang and S. Zhang, ICIP 2010
参考:
[1] 水平集方法 - WiKi
[2] Level Set Method - 1
[3] Level Set Method - 2
[4] Level Set (水平集)算法是什么? 知乎
[5] Level Set Method: Explanation - Herve Lombaert
[6] Level Set Methods: An initial value formulation
[7] Digital Image Processing
[8] Segmentation in Medical Imaging
大佬:
[1] Kaihua Zhang
[2] Chunming Li
[3] Chunming Li (Matlab)
[4] Lei Zhang










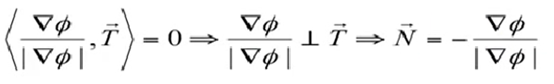

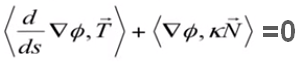



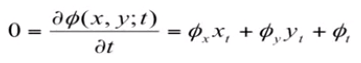
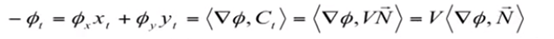



















 3433
3433

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










