【干货】分享几个免费下载音乐mp3的网站实测可用

最新推荐文章于 2025-04-04 19:16:50 发布
最新推荐文章于 2025-04-04 19:16:50 发布
阅读量2.4w 收藏 3
点赞数
分类专栏： 音乐 音乐下载 mp3 文章标签： 音视频 腾讯会议 音频
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_31708763/article/details/134158407
版权

简述

本文仅用于学习交流，不做任何声明。

分享几个免费下载音乐mp3的网站、免费音乐、

大家有找不到资源的，可以留言评论下，帮忙代下载~~

一说

文本由PUSDN强力驱动！

有账号的朋友，可以点个赞或者评论两句哦，评论后会获得积分奖励～

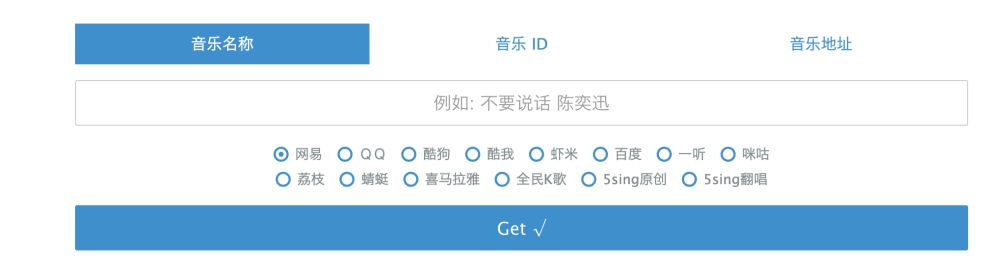
wandhi【实测可用】

评价：比较推荐，无需登录，歌曲较全，也是笔者经常用的网站

网址：http://music.wandhi.com/

e7b04045b2316646b7eb5b5232c45a82.jpeg

哈基米

https://www.dtshot.com/

1e78501b3b0bc95ec8d49d9ed5a9cd0a.jpeg

pixabay

听说很强大， 4万+音乐

https://pixabay.com/

淘声

https://www.tosound.com/

https://mixkit.co/

爱给

https://www.aigei.com/

c26d0358bed9089e8cf4720b388562fe.jpeg

其他

https://www.jamendo.com/start

Spring Boot进阶(42)：如何实现图片在线下载？
**My Coding Family**
09-05 3884
如何实现图片在线下载？一文教会你。
【超级干货】播放器核心知识点-音视频同步原理深入剖析
q2nAmor
03-11 441
本文在反复理解的基础上顺便对网上的一些不正确的解释和说法进行了勘误，对模糊的地方进行了澄清，基本上示例中的每一行代码为什么这么写，它的依据是什么都有明确的解释。完整源码链接：https://gitpub.sietium.com/bridge/ffsync。
在线音乐网站
12-07
功能介绍： 用三层架构简单实现在线音乐平台能够播放音乐，百度推广分享，后台管理等 后台功能：歌曲管理 歌手管理 歌曲类型管理 安全管理 歌手类型管理 后台页面设计仿制liuwt999的三层架构音乐平台 希望各位大神可以多多指点，谢谢！
6个免费的音乐下载网站，一键下载MP3歌曲
m0_37667089的博客
04-11 16万+
你可以在这里找到最近正在热门的音乐，还能看到推荐的歌手、单曲推荐，热门歌单等，喜欢的音乐可以直接点击播放，或点击单曲后面的三个点击就可以看到下载按钮，支持免费下载单曲、歌词、封面等详细内容。页面左侧提供了超详细的音乐分类，包括民谣、电子乐、古典、电影、爵士乐、嘻哈、流行、民族等不同风格的音乐，还支持强大的音乐搜索，输入歌曲的英文名字或歌手就可以找到相关的音乐。一个非常强大的音乐搜索网站，支持搜索各大平台的音乐，支持输入歌名、歌手、ID、音乐地址等详细信息搜索单首歌曲，搜索到的歌曲支持在线播放以及免费下载。
8个免费下载无损歌曲的网站，值得收藏
凸比难拨弯
09-27 10万+
支持免费下载整首专辑以及各种格式的无损音乐，提供的音乐包括粤语歌曲、英文歌曲、经典歌曲，每周都会定期更新音乐专辑，基本上想听的音乐都能在这里找到。打开页面可以看到当下流行的音乐单曲，还支持强大的音乐搜索功能，下载方式简单，每首歌曲都提供了下载按钮，可以下载多种格式的无损音乐。一个聚合了免费的音乐、视频资源的网站，能够找到大部分的想听的营业，所有的营业都能免费播放。
告诉大家一个MP3音乐集合包打包下载网址
chenqingjie123的博客
05-12 1万+
告诉大家一个MP3音乐集合包打包下载网址
免费下载mp3音乐的6个网站，国内外各种类型的音乐都有！
热门推荐
qq_32450471的博客
12-01 60万+
免费听歌
免费听音乐，下载音乐mp3，mp4，歌词的网站分享（2024-04-22）
hap1994的博客
04-22 13万+
免费听和免费下载,mp3,mp4,歌词下载
一个好用的MP3音乐下载网，我推荐给你（免费）
2301_81185531的博客
09-25 3305
非常好用，无需登录。
7免费的无损音乐下载网站，建议收藏！
qq_40374677的博客
10-19 5万+
一个页面超干净的免费音乐网站，可以在短时间内找到自己想要的音乐。不仅涵盖了最新的热门歌曲，也有一些老歌和小众歌曲。一个页面超干净的免费音乐网站，可以在短时间内找到自己想要的音乐。不仅涵盖了最新的热门歌曲，也有一些老歌和小众歌曲。
免费音乐下载网站分享（MP3文件格式）
weixin_51293134的博客
09-14 3609
最近需要下载一些歌曲，发现很多音乐app上下载文件都需要vip，再上网查询了一番，最后发现了一个宝藏网站，可以免费下载各种格式的MP3文件，在这里给大家分享一个网址。可能有像我一样的需要对MP3文件进行编辑，又不想通过下载app进行剪辑的，我找到了一个免费的网站，次数基本够用，真心不错，导出来的也是MP3格式，在这里也分享给大家。[MP3文件编辑网站]（https://www.aigei.com/tool/audio/trim）网站贴心给大家提供了讲解视频，真心不错！
下载音乐_下载音乐_
10-03
可以通过网路爬虫的方式，下载某一个网站上想要下载的音乐。
MP3音乐采集器
02-04
上次做KTV的程序没有 自动下载 歌曲的功能。这里附上 下载歌曲的代码
WAV 格式歌曲
04-20
WAV 格式音频，超过60M，压缩后刚好。
最新音乐下载
04-03
打开软件，搜索你想搜索的音乐即可下载
程序员写代码与厨师做菜、音乐家作曲、诗人写诗——其实，这是一篇程序员做饭指南
AI天才研究院
04-07 2万+
作为程序员，编写代码可以被视为一种创造性的活动，与厨师做菜、音乐家作曲、诗人写诗有许多相似之处。厨师需要选择正确的食材，并根据食材的特性决定如何处理它们，以制作出美味的菜肴。同样，程序员需要选择正确的编程语言和库，并根据它们的特性决定如何使用它们，以编写出高效的软件。音乐家需要了解音乐理论和乐器，以创作出令人愉悦的音乐。同样，程序员需要了解算法和数据结构，以编写出高效、可读性强的代码。诗人需要掌握语言和文学技巧，以创作出令人动容的诗歌。
【腾讯Bugly干货分享】微信终端跨平台组件 mars 系列(二) - 信令传输超时设计
腾讯Bugly的专栏
12-19 2216
本文来自于腾讯Bugly公众号（weixinBugly），未经作者同意，请勿转载，原文地址：http://mp.weixin.qq.com/s/9DJxipJaaBC8yC-buHgnTQ 作者简介： 曹少琨，微信移动客户端开发工程师，2014年加入腾讯，从事手Q跨平台移动服务框架 MSF 的开发及优化工作，2015 年转入微信终端基础开发组参与网络组件的开发及维护工作。 前言mars 是微信官
万字回顾中国生成式AI大会！50+大咖演讲精华干货爆棚，来没来都值得收藏
最新发布
强化学习曾小健
04-04 706
中国生成式AI的每一次突破，从来不是某家企业的独角戏，而是产学研用协同攻坚的交响曲。开年DeepSeek的爆火，成为中国乃至世界生成式AI产业的关键拐点。它颠覆了“堆砌算力”的固有路径，开辟出一条“效率优先”的创新路径，催化开源、推理模型与AI Infra研发热潮，更为端侧AI与国产AI算力基础设施的落地应用注入了新动能。站在技术与产业共振的历史节点，我们每一个人，都正在见证和参与一场激动人心的技术跃迁。春天来了，生成式AI的浪潮更加波涛汹涌，未来正呼啸而至。
如何免费下载mp3格式的歌曲?整理了4个不同的方法~
嗨格式数据恢复大师
02-26 1万+
为了畅听音乐和无阻碍使用音频，在这个过程中我们就会遇到这样一些问题：歌曲到期无法听怎么办？下载的音频格式太陌生冷门，无法在其他平台设备上播放和使用怎么办？下面就向大家介绍一些免费听歌的网站和软件以及如何下载网页音乐、如何把不同格式的音频转换成MP3这四个问题，一站式解决音频播放、编辑、上传、分享问题。
哈密尔顿函数与变分法的联系
06-10
哈密尔顿函数是经典力学中的一个非常重要的概念，它与变分法密切相关。 首先，我们来看哈密尔顿函数的定义。对于一个具有广义坐标$q_i$和广义动量$p_i$的系统，哈密尔顿函数$H(q,p)$定义为： $$H(q,p) = \sum_i p_i \dot{q}_i - L(q,\dot{q})$$ 其中，$L$是系统的拉格朗日函数。哈密尔顿函数是一个关于广义坐标和广义动量的函数。 接下来，我们来看哈密尔顿函数与变分法的联系。在经典力学中，哈密尔顿原理是指系统在某个时间段内的运动路径，使得作用量最小。作用量$S$是一个关于路径$q(t)$的函数，定义为： $$S[q(t)] = \int_{t_1}^{t_2} L(q,\dot{q})dt$$ 其中，$L$是系统的拉格朗日函数。 利用变分法可以得到哈密尔顿原理的欧拉-拉格朗日方程，即： $$\frac{\delta S}{\delta q} = \frac{d}{dt}\frac{\delta S}{\delta \dot{q}}$$ 将$L$表示为哈密尔顿函数的形式，即$L(q,\dot{q})=p\dot{q}-H(q,p)$，其中$p$是广义动量，代入作用量的表达式中，可以得到： $$S[q(t)] = \int_{t_1}^{t_2} [p\dot{q}-H(q,p)]dt$$ 接下来，我们对路径$q(t)$进行微小变化$\delta q(t)$，并保持端点不变。利用变分法，可以得到： $$\delta S = \int_{t_1}^{t_2} [\delta p\dot{q} + p\delta \dot{q} - \frac{\partial H}{\partial q}\delta q - \frac{\partial H}{\partial p}\delta p]dt + [p\delta q]_{t_1}^{t_2}$$ 根据变分法的要求，端点不变，即$[p\delta q]_{t_1}^{t_2}=0$。因此，我们可以得到哈密尔顿原理的欧拉-拉格朗日方程： $$\begin{cases}\frac{\partial H}{\partial p}=\dot{q}\\-\frac{\partial H}{\partial q}=\dot{p}\end{cases}$$ 这就是哈密尔顿函数与变分法的联系。使用哈密尔顿函数，可以将拉格朗日方程转化为哈密尔顿方程，从而更方便地研究系统的动力学性质。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

JaneYork

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值