BST(二叉搜索树)的构建和应用

氨基蝶呤

于 2025-05-16 18:02:29 发布

阅读量799

点赞数 37

文章标签：数据结构 c++ BST 二叉树二叉搜索树

本文链接：https://blog.csdn.net/2402_89294789/article/details/148008691

版权

什么是二叉搜索树？

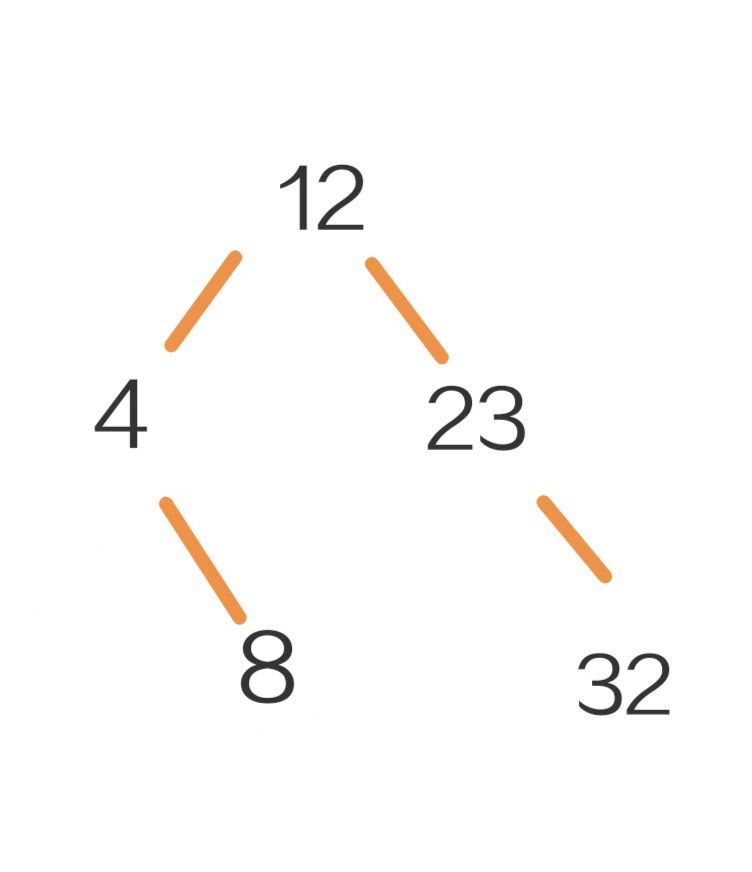
例如：把以下5个关键字构成一棵二叉搜索树，先把12放到根结点，23比12大，作为12的右孩子，32比12大，比23大，作为23的右孩子,4比12小，作为12的左孩子，8比12小，比4大，作为4的右孩子。

12 23 32 4 8

手动构造BST就实现了。根据以上这个例子，我们可以明确BST的一些性质：

左小右大：每个结点的左孩子比它小，右孩子比它大，推广一下，每个结点左子树的所有结点都比它小，右子树的所有结点都比它大
每次插入一个结点的时候，这个结点都是以叶子结点被插入进去的
BST的查找效率和它的树型有关，比如你试一下依次插入1,2,3,4,5和2,1,3,4,5和3,1,4,2,5

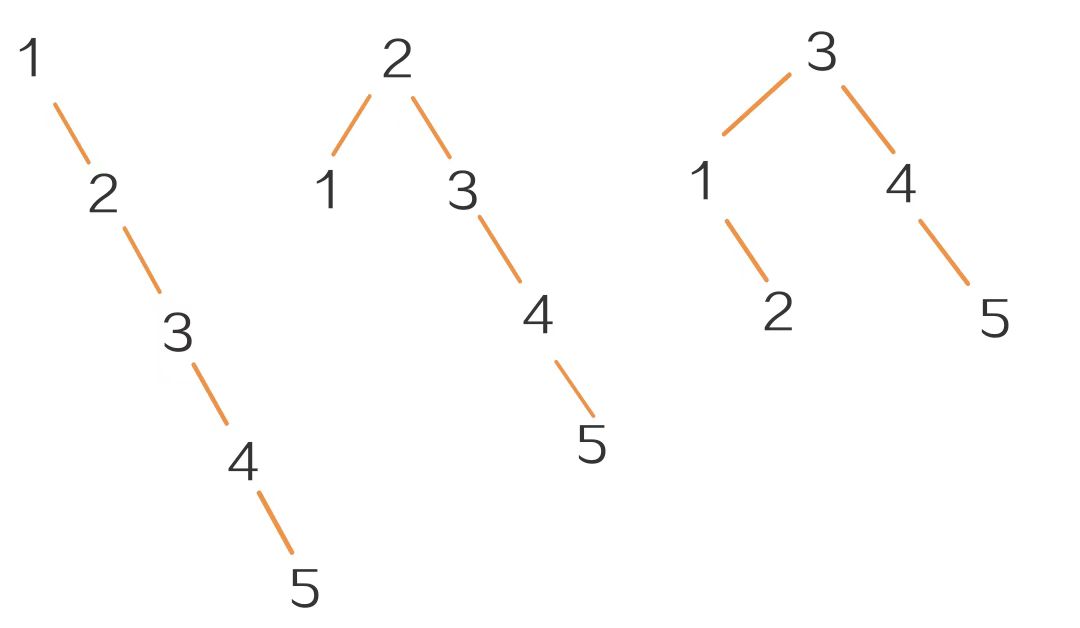
其等概率查找成功的平均查找长度分别为：(1*1+1*2+1*3+1*4+1*5)/5=3

(1*1+2*2+1*3+1*4)/5=12/5[一个元素(2)被比较一次就能找到，两个元素(1 3)被比较两次才能找到,一个元素(4)被比较三次才能找到,一个元素(5)被比较四次才能找到]

(1*1+2*2+2*3)/5=11/5

说明树型的不同导致了查找效率的不同，前者查找长度大，效率低下，退化成了链状结构，和在数组里遍历查找关键字的时间复杂度是一样的，都是O(n),失去了树型结构的优越性。

BST为完全二叉树时，平均比较次数为O(logn)

因为对于有n个结点的完全二叉树，层数为[logn]+1,对于最后一层的元素，被查找的次数就是[logn]+1.那么logn就是平均比较次数的数量级

和上一条性质综合来看，我们能得到结论：将n个关键字构成BST,链状结构越少，也就是越接近完全二叉树的形状，效率就越高，其实这就是折半查找判断树.(我下次来说这个算法)

下面我们思考一下二叉搜索树如何用代码来实现。

题目描述

输入 n 个非负整数作为关键词，建一棵基于这些关键字的二叉搜索树 (Binary Search Tree)。注意重复的关键字不插入 BST 中。

输入格式

第一行包含一个整数 n(1≤n≤10000)，表示关键词的个数。第二行包含 n 个整数 k1,k2,⋯,kn(0≤ki<500)，表示每个关键词。

输出格式

第一行输出 BST 中元素的个数，第二行输出 BST 的先序遍历序列。

样例输入：6
12 23 32 4 8 12

样例输出：5
12 4 8 23 32

发现输入有重复，怎么办？

在插入前，先在BST里搜索一遍，没有查找到关键字就插入，否则不做操作。

查找可以以这样的思路：遍历到某个结点T的时候，将它对应的数值T->data和要查找的关键字key作对比，相等就返回1，key较小就继续在左子树里查找，否则就继续在右子树里查找。因为右子树的所有结点都比 data大，是不可能找到key的。如果没有找到关键字，那么最后遍历到的那个结点的孩子结点就是key要插入的位置，至于是左孩子还是右孩子，就要通过比较大小来得到。

主要的函数如下：

int SBST(BT T,int key,BT f,BT &p){//查找函数,也是一个回调函数

//f是T的双亲结点，初识调用值为NULL

//p采用传址调用
   if(!T){
   p=f;
   return 0;
   }
   else if(key==T->data) return 1;
   else if(key<T->data){
       return SBST(T->lchild,key,T,p);
   }
   else return SBST(T->rchild,key,T,p);
}

int InsertBST(BT &T,int e,int &count){//插入函数
   BT p=NULL;
   if(!SBST(T,e,NULL,p)){
       BT s=(BT)malloc(sizeof(BiTree));
       s->data=e;
       s->rchild=NULL;
       s->lchild=NULL;
       if(!p) T=s;
       else if(e<p->data) p->lchild=s;
       else p->rchild=s;
       count++;//计数
       return 1;
   }
   return 0;
}

最开始的时候树为空，第一轮查找之后,p返回的值为NULL,SBST返回0，执行插入操作。!p=true，根节点的data就被成功赋值为了关键字12

第二轮查找中，4<T->data,继续在左子树查找，然而左孩子为NULL,没有找到，p被更新为这个没有左孩子的结点T,那么4就被插入为左孩子。

以此类推，最后一个查找的值是12，在BST中已存在，就不再做插入操作。

完整代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef struct BiTree{
	int data;
	BiTree*lchild,*rchild;
}BiTree,*BT;
int SBST(BT T,int key,BT f,BT &p){//查找函数
	if(!T){
	p=f;
	return 0;
	}
	else if(key==T->data) return 1;
	else if(key<T->data){
		return SBST(T->lchild,key,T,p);
	}
	else return SBST(T->rchild,key,T,p);
}
int InsertBST(BT &T,int e,int &count){//插入函数
	BT p=NULL;
	if(!SBST(T,e,NULL,p)){
		BT s=(BT)malloc(sizeof(BiTree));
		s->data=e;
		s->rchild=NULL;
		s->lchild=NULL;
		if(!p) T=s;
		else if(e<p->data) p->lchild=s;
		else p->rchild=s;
		count++;
		return 1;
	}
	return 0;
}
void PreOrder(BT T){//先序遍历
	if(T){
		cout<<T->data<<" ";
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}
int main(){
	BT T=NULL;
	int n,e,count=0;
	cin>>n;
	while(n--){
	cin>>e;
	InsertBST(T,e,count);	
	}
	cout<<count<<"\n";
	PreOrder(T);
	return 0;
}

在主函数中，输入关键字的个数n，遍历n次，每次调用插入函数，最后输入结点个数并用先序遍历输出BST。

这个算法是清华大学出版社的数据结构书上的，简洁高效，我主要是写了自己对代码关键部分的理解。欢迎大家一起来学习讨论！(其实本人在写这篇文章之前搜了一下看有没有人写，想着如果很多人写那我就不写了吧，结果有看到一个很多赞的大佬写得特别详细，包括更详细的分析和删除节点的算法，但是那个代码对于我这种菜狗来说简直太陌生了，然后我就想着写一篇初学者能看得懂的，下次我会更新折半查找判断树的算法(其实0人在意))