解题报告：POJ_3904 Sky Code 莫比乌斯反演|容斥

题目链接

题意：

给定n个数，要求从中选出4个数，使得这4个数的最大公因子为1，求满足条件的组数。

思路：

简单的容斥，用f(x)表示最大公因子为x的倍数的组数，那么答案为：

ans =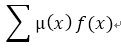

代码：

#include<cstdio>
#include<vector>
#include<cstring>

using namespace std;

const int N = 1e4+10;
int mu[N];
bool Np[N];
vector<int>pr;
vector<int>E[N];
int num[N];
void init(){
   mu[1] = 1;
   for(int i=2;i<N;i++){
      if(!Np[i]){
         pr.push_back(i);
         mu[i] = -1;
      }for(int j=0;j<pr.size();j++){
         int t = pr[j] * i;
         if(t>N)break;
         Np[t] = true;
         if(i%pr[j]==0){
            mu[t] = 0;
            break;
         }mu[t] = -mu[i];
      }
   }
   for(int i=1;i<N;i++){
      for(int j=i;j<N;j+=i){
         E[j].push_back(i);
      }
   }
}

long long C(int n){
   if(n<4)return 0;
   long long res = 1;
   for(int i=0;i<4;i++){
      res *= (n-i);
   }for(int i=2;i<=4;i++){
      res /= i;
   }return res;
}

int main()
{
   init();
   int n,x;
   while(scanf("%d",&n)==1){
      memset(num,0,sizeof(num));
      int m = 0;
      while(n--){
         scanf("%d",&x);m = max(m,x);
         for(int i=0;i<E[x].size();i++){
            int j = E[x][i];
            num[j]++;
         }
      }long long ans = 0;
      for(int i=1;i<=m;i++){
         if(mu[i]){
            ans += 1LL * mu[i] * C(num[i]);
         }
      }printf("%lld\n",ans);
   }return 0;
}