题意:
给一个4*n的表格,你有两种矩阵(1*2),(2*1),询问放满的方案数。
n<=1e9
思路:
显然公式应该是一个线性递推方程,知道后可以用矩阵快速幂在O( log(n) * m^3 )求得答案(m为方程的项数)
为了求这个方程,我们可以用轮廓线DP求的方程的前k项
然后假设一个k>m,用高斯消元求k*k的矩阵的秩,从而求得m
再用高斯消元求得方程即可
求的方程为
代码:
#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
void init(){
int dp[100][16]={0};
dp[1][0]=dp[1][3]=dp[1][6]=dp[1][12]=dp[1][15]=1;
for(int x=2;x<=16;x++){
for(int i=0;i<16;i++){
dp[x][i] += dp[x-1][i^15];
for(int j=0;j<3;j++){
if((i&(1<<j))&&(i&(1<<(j+1)))){
int t = i^(1<<j)^(1<<(j+1));
dp[x][i] += dp[x-1][t^15];
//if(x==2)printf("%d is from %d\n",i,i^(1<<j)^(1<<(j+1)));
}
}//printf("dp[%d][%d]--->%d\n",x,i,dp[x][i]);
}dp[x][15]+=dp[x-1][15];
printf("dp[%d]--->%d\n",x,dp[x][15]);
}
}
namespace fast_Matrix{
int n=4;
const int MAX_E = 4;
inline void debug(long long a[MAX_E][MAX_E]){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
printf("%I64d%c",a[i][j],j!=n-1?' ':'\n');
}
}printf("\n");
}
long long ans[5]={1,1,5,11,36};
long long fast_mat(long long y)
{
long long tmp[MAX_E][MAX_E]={0};
long long mut[MAX_E][MAX_E]={
1,5,1,mod-1,
1,0,0,0,
0,1,0,0,
0,0,1,0,
};
long long res[MAX_E][MAX_E]={0};
for(int i=0;i<n;i++){
res[i][i] = 1;
}
while(y){
if(y & 1){
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
tmp[i][j] = res[i][j];
memset(res,0,sizeof(res));
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)if(tmp[i][j])
for(int k = 0; k < n; k++)
res[i][k] = (res[i][k] + tmp[i][j] * mut[j][k])%mod ;
}
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
tmp[i][j] = mut[i][j];
memset(mut,0,sizeof(mut));
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)if(tmp[i][j])
for(int k = 0; k < n; k++)
mut[i][k] = (mut[i][k] + tmp[i][j] * tmp[j][k])%mod ;
y >>= 1;
}
long long val = 0;
for(int i=0;i<n;i++)val = (val+res[0][i]*ans[n-i-1])%mod;
return val;
}
}
using namespace fast_Matrix;
int main()
{
init();
long long t;
while(scanf("%lld",&t)==1){
if(t>=3)printf("%lld\n",fast_mat(t-3));
else printf("%lld\n",ans[t]);
}return 0;
}










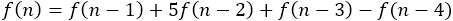














 532
532

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








