cs231n 2023春季课程理解——lecture_4

引言

在上一篇cs231n 2023春季课程理解——lecture_3文章中，我讲解了关于优化算法的一些内容。在这篇文章中，我们开始来介绍深度学习，其中包含了反向传播以及神经网络等相关知识。

深度学习现阶段发展的成果

在讲神经网络之前，先给大家简单看一些深度学习现阶段的应用，让我们通过这些应用来了解目前深度学习有哪些好玩的地方：



上面三张图片展示了目前深度学习的一些强大应用(当然，实际上也不止这些)。第一张图片是一个文本生成图片模型，你可以通过一段话的描述，来生成一张图片(感觉是手残党的天堂)；第二张是今年(2023)新出的一个大语言模型，你可以向它问问题(包括一些代码如何去编写等)，它能给你一个答案(不过它是要钱的，你可以去使用它的阉割版,ChatGPT3.5(至少截止至目前它是免费的，只不过需要科学上网))；第三张也是今年新出的一种模型，俗称分割一切，它与以往的分割模型只能分割出一种特定类型的图片不同，它可以分割所有类型的图像(当然，具体我也没有去尝试，所以就不多讲了)。
现在，了解了深度学习的应用之后，我们在一起去探索具体的神经网络吧。

神经网络

到现在为止，我们已经讲过了线性分数函数：$f=Wx$ ，其中，$x\in R^D$, $W\in R^{C\times D}$，而且我们也一直将其视作我们想优化的函数的一个事例。那么，如果我们想要使用神经网络，我们可以将它(就是前面的这个函数)看作是一个线性变换。最简单的形式，就是将两个线性变换叠加到一起，此时神经网络的相关函数就是 $f=W_2\max (0,W_{1}x)$ ，其中，$x\in R^D$, $W_1\in R^{H\times D}$，$W_2\in R^{C\times H}$(在实际中我们通常会在每一层加上一个偏置项b)。
注： 上面的两层神经网络的函数表达式是非线性的，那么我们为什么要非线性的呢？其实是因为线性函数对于一些类别不能区分(如下图)，使用非线性函数之后，就能将它们按照特征分类，再使用线性函数区分开了。

神经网络其实是一个非常宽泛的术语，更加精确的叫法其实是全连接网络或者是多层感知机(MLP)。
在上面我们知道了全连接网络是由多个线性层叠加到一起的。所以，全连接网络的计算方式就是分层计算，具体地讲，就是类似于采用矩阵的方法将线性层相乘。其细化过程如下图：

好，我们现在了解了两层的全连接层是怎么样子的，应该如何去计算。那么三层呢？对的，我们可以用类比的思想，在两层的基础上再加一层线性变换就好了。此时它就应该是 $f=W_3\max (0,W_2\max (0,W_{1}x))$ ，其中$x\in R^D$, $W_1\in R^{H\times D}$，$W_2\in R^{H_2\times H_1}$，$W_2\in R^{C\times H_2}$。
现在，有一个问题。你应该看到了两层的全连接层有一个max函数，三层的里面有两个。那么，为什么这个max函数这么重要呢？其实，这个max函数叫做激活函数，有了它，才能区分非线性。否则，最终还是线性分类。(如果没有这个激活函数，最终就是$f=W_n{W}_{n-1}...W_{1}x=Wx$，其中$W=W_n{W}_{n-1}...W$)
下面是神经网络结构图：

常见激活函数

既然讲到了激活函数，那就对激活函数进行一个简单的了解一下吧(这里的了解指的是先知道有这么个东西，具体的我们之后再讲)。一些相关的激活函数以及其公式如下图(其中ReLU对于大多数问题来说都是一个不错的选择(不过好像Sigmod函数也用的比较多))。

神经网络代码的实现

我们首先先实现以下神经网络的计算，以三层网络模型(图在上面)为例：

# 三层神经网络的前向传播计算
f = lambda x: 1.0/(1.0 + np.exp(-x)) # 设置激活函数(Sigmod)
x = np.random.randn(3, 1) # 随机生成一个3×1形状的输入数据
h1 = f(np.dot(W1, x) +b1) #计算第一个隐藏层(h1的形状为4×1)
h2 = f(np.dot(W2, h1) +b2) #计算第二个隐藏层(h2的形状为4×1)
out = np.dot(W3, h2) +b3 #最终输出(形状为1×1)

现在，我们来写一个完整的2层神经网络的代码(大概20行，且没有添加偏置项)：

import numpy as np
from numpy.random import randn

N, D_in, H, D_out = 64, 1000, 100, 10
x, y = randn(N, D_in), randn(N, D_out) # 随机生成数据
W1, W2 = randn(D_in, H), randn(H, D_out) # 随机生成权重

for t in range(2000):
	h = 1 / (1 + np.exp(-x.dot(W1)))
	y_pred = h.dot(W2)
	loss = np.square(y_pred - y).sum()
	print(t, loss)

	grad_y_pred = 2.0 * (y_pred - y)
	gred_w2 = h.T.dot(grad_y_pred)
	grad_h = grad_y_pred.dot(W2.T)
	gred_w1 = x.T.dot(grad_h *h *(1 - h))

	w1 -= 1e-4 * grad_w1
	w2 -= 1e-4 * grad_w2

在上述代码中，最开始两行是引入相关库，之后的三行代码(4-6行)是定义了一个两层的网络结构，而循环中的第1到第3行(9-11)代码是前向传播的计算，之后再输出当前循环的次数以及计算出的损失值，再之后的四行代码(14-17)，则是计算梯度(分析梯度法计算的)，最后两行是进行梯度下降。

神经网络与真实的神经对比

神经网络其实是受生物神经系统启发的。现在我们来看下图：

在图中的左上角是生物神经元(neuron)，它是大脑的基本计算单位 。在人类的神经系统中，大约有 860 亿个神经元，它们被大约1014个突触(synapses)连接起来。从图中我们可以看到，每个神经元都从它的树突(dendrites) 获得输入信号，然后沿着它的轴突(axon) 产生输出信号。轴突在末端会逐渐分枝，通过突触和其他神经元的树突相连。这样就完成了信息的传输。那么现在我们看看右下方的神经网络模型(一个数学模型，简化版)，它也是以类似的方式在不同节点之间相互连接，传递信息。例如，在突触上面传递的信号($x_0$)，在与突触($w_0$)相结合后，生成一个新的信号(与之前的信号有关联,如$w_0{x}_0$)，所有的信息在细胞体(cell body)中集合之后，通过在顶部应用激活函数来输出对应的值，最终输出到轴突中。
下图是生物神经元的组合以及神经网络的结构图的对比：

在神经网络中添加损失函数

现在我们了解了损失函数，规则化以及全连接网络(神经网络)，为了防止忘记它们的公式，我们来看一下图：

在上图中，我们知道了损失函数、正则化损失以及全连接网络的公式。现在，让我们考虑一下，如果把损失函数添加到全连接网络中，我们怎么去计算梯度呢(毕竟如果可以计算出$\frac{\partial L}{\partial W_1}$, $\frac{\partial L}{\partial W_2}$，那么我们就可以学习$W_1$和$W_2$了)？
这里有一个非常容易的方法，那就是暴力求解(直接在纸上求出${▽}_{W}L$)。其具体求解过程如下图：

这种暴力求解虽然可以求出来，但是它还是会有着许多问题(毕竟是暴力求解嘛，最无脑的操作)。比如说，计算很繁琐：在整个计算过程中有着大量的矩阵，需要大量的纸张；如果改变损失函数，那么需要重新计算；对于复杂的模型非常不可行(巧了，深度学习中的模型就没有不复杂的)。
一个更好的方法是用神经网络计算图结合反向传播算法来计算。具体形式如下图：

计算图，这个好理解，就是将神经网络计算的过程用图表示出来(上图的这个形式就是了)。那么反向传播呢，这个是什么？关于反向传播，请见下节详细讲解。

反向传播

根据上文我们知道，根据反向传播可以计算出${▽}_{W}L$，那么，反向传播是什么呢？反向传播，是一种通过链式求导法则来递归求导复杂函数的梯度的方法，即逐层求出目标函数对各神经元权值的偏导数，构成目标函数对权值向量的梯度。之所以需要反向传播，是因为它可以对权值的优化提供依据。

链式求导法则

既然反向传播算法使用了链式求导法则，那么这里就简单的说一下链式求导法则。通俗地讲，它其实就是由多个简单式子结合在一起。如：
假设y=g(x)，z=h(y)(其实也就是z=h(g(x)))，则有:
$$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial x}$$
类似的，假设x=g(s)，y=h(x)，z=k(x, y)，那么有：
$$\frac{\partial z}{\partial s}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}+\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}$$
这就是链式求导的公式。

标量形式的反向传播

知道了链式求导法则，那么我们现在来正式地学习一下反向传播。

简单例子

首先，我们来看一个简单的例子(都是标量，即一个数值，而不是向量，当然向量的形式也是一样的计算)：现在假设有这么一个函数$f(x,y,z)=(x+y)z$。我们赋值x = -2，y = 5，z = -4。它的反向传播是怎么计算的呢，我们来看下图(结合了计算图的形式，更容易理解了)，并对它进行分析。

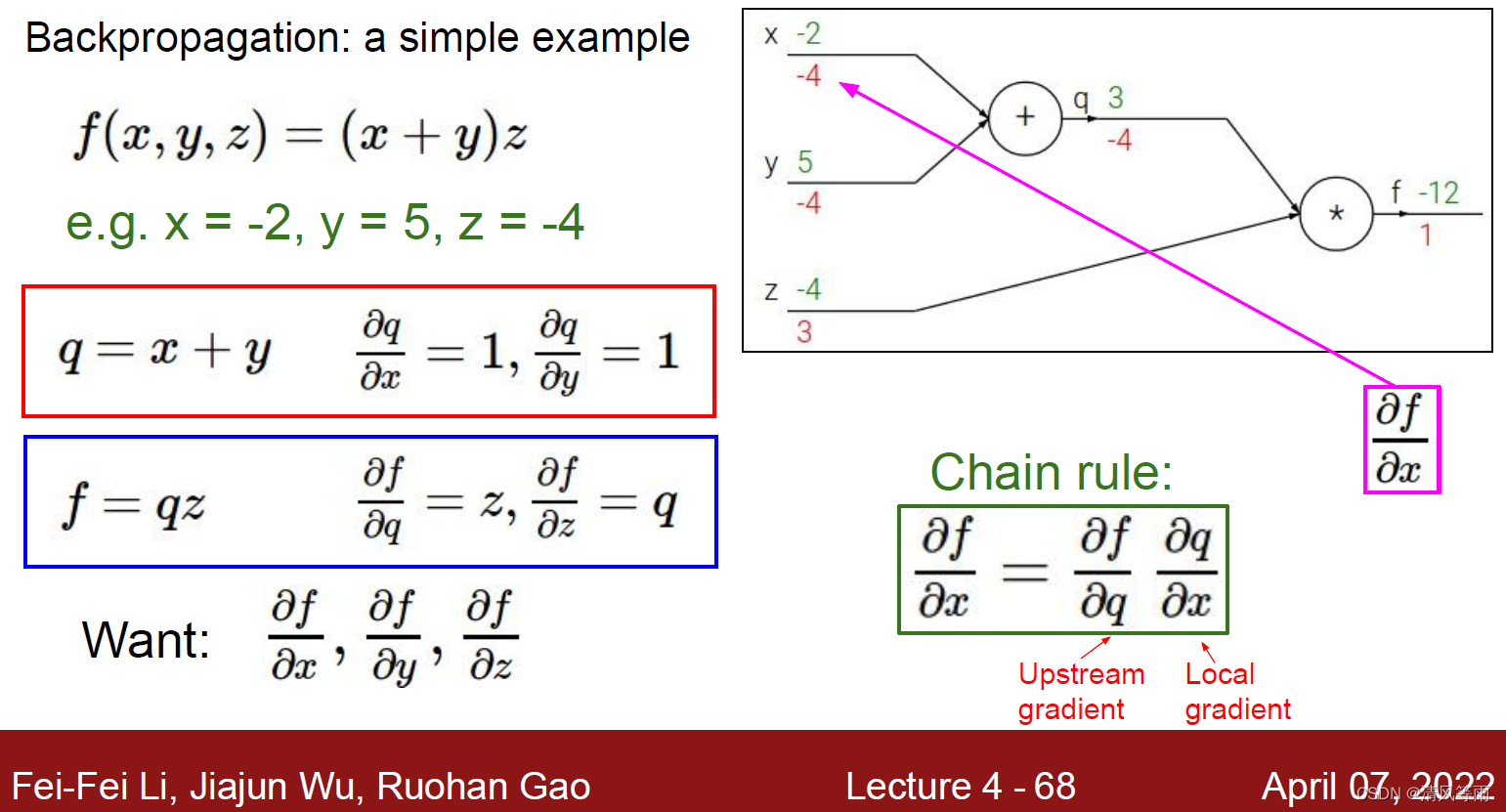
在上图的右上角中，我们看到了这个例子的计算图。现在我们假设q=x+y，那么f = qz。通过这两个简单的公式，我们能求得$\frac{\partial q}{\partial x}=1$, $\frac{\partial q}{\partial y}=1$, $\frac{\partial f}{\partial q}=z=-4$, $\frac{\partial f}{\partial z}=q=-2+5=3$。根据我们的求导公式以及链式求导法则，我们可以算出f点出的梯度$\frac{\partial f}{\partial f}=1$, q处的梯度(当然，只计算它没有任何意义，因为我们根本不关注它，它只是用链式法则求$\frac{\partial q}{\partial y}$以及$\frac{\partial q}{\partial x}$的一部分)$\frac{\partial f}{\partial q}=-4$, x点处的梯度$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}=-4\times 1=-4$, y处的梯度$\frac{\partial f}{\partial y}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial y}=-4\times 1=-4$以及点z处的梯度$\frac{\partial f}{\partial z}=q=3$。
以上就是反向传播的计算过程。它是从尾部开始计算的(图中右上部分的红色数字就是梯度)，然后一直到输入端(x, y, z)。同理，前向传播就是从头开始计算(绿色字体)，一直到最终的输出(f)。下面，用一段代码来实现这个例子：

# 设置输入值
x = -2; y = 5; z = -4

# 执行前向传播的计算
q = x + y # q的值变为3
f = q * z # f的值变为-12

# 以与前向传播的计算过程相反的方式来计算反向传播:
# 首先计算f = q * z的反向传播
dfdz = q # df/dz = q, 所以z上的梯度就是3
dfdq = z # df/dq = z, 所以q上的梯度就是-4
dqdx = 1.0
dqdy = 1.0
# 现在计算q = x + y的反向传播
dfdx = dfdq * dqdx  # 会进行相乘是因为链式求导法则
dfdy = dfdq * dqdy  

反向传播的直观理解

根据上面的例子我们可以看出，我们在反向传播中做的其实就是计算图中的每个节点的梯度，但是每个节点都是，但是每个节点都是只知道附近的情况(例如上面的例子中，f就不知道x和y的情况，所以我们在每个节点都有流入这个节点的输入值以及流出的输出值。那么，当我们知道了局部的输入(x, y)输出(z)，以及当前的梯度，那么我们就能计算出z相对于x以及相对于y的梯度。因此，可以将反向传播看成是一个局部的过程(慢慢的组合起来)。其具体形式如下图：

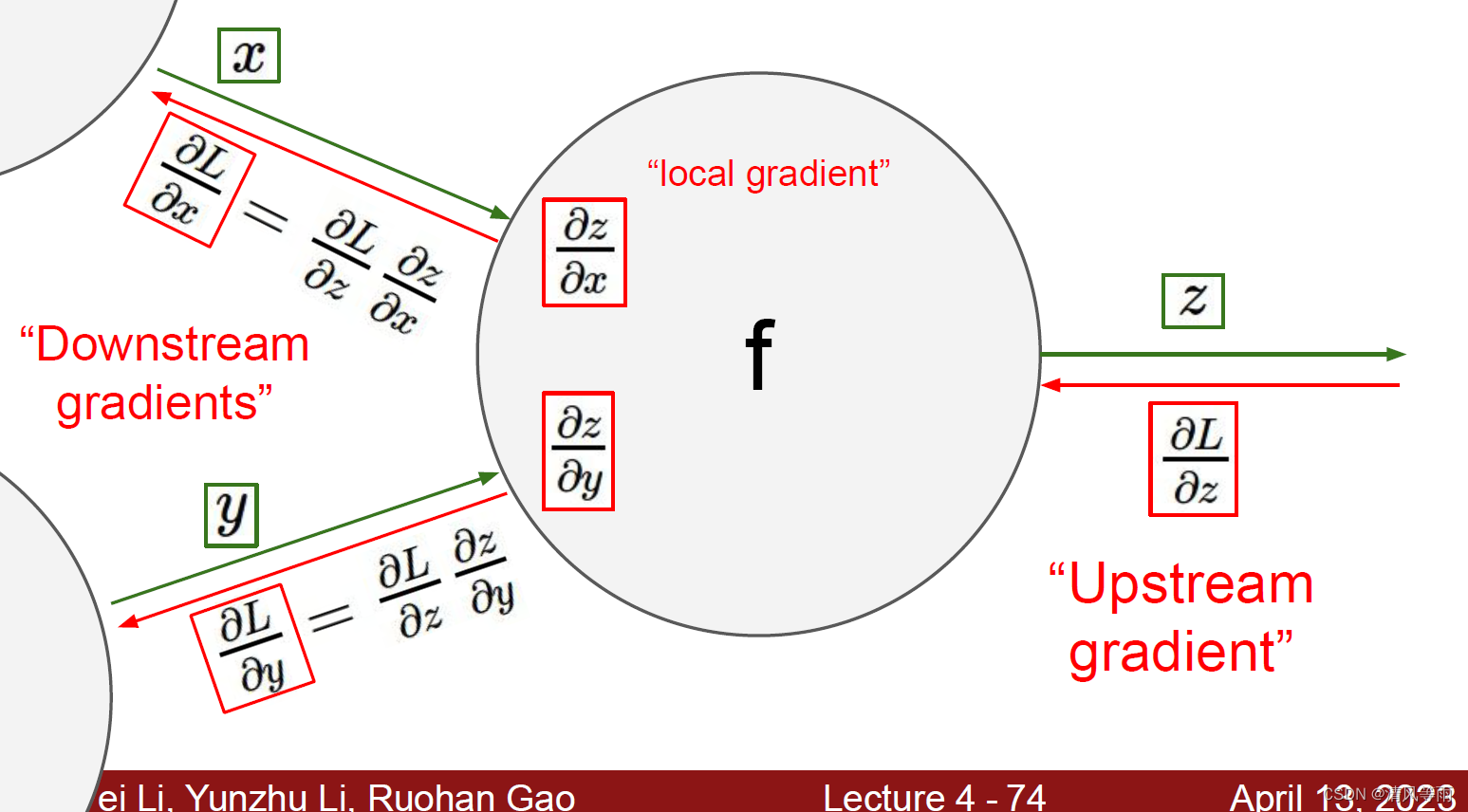
复杂例子

通过简单的例子我们了解了反向传播的计算过程，那么，现在我们在使用一个复杂一点的例子(当然现在还是标量)来巩固一下，同时通过它我们也能知道为什么反向传播作用那么大。假设有这么一个公式：$$f(w,x)=\frac{1}{1+e^{-(w_0{x}_0+w_1{x}_1+w_2)}}$$
那么根据这个公式我们可以得到计算图如下图(同时一些新的函数的导数也在图中)：

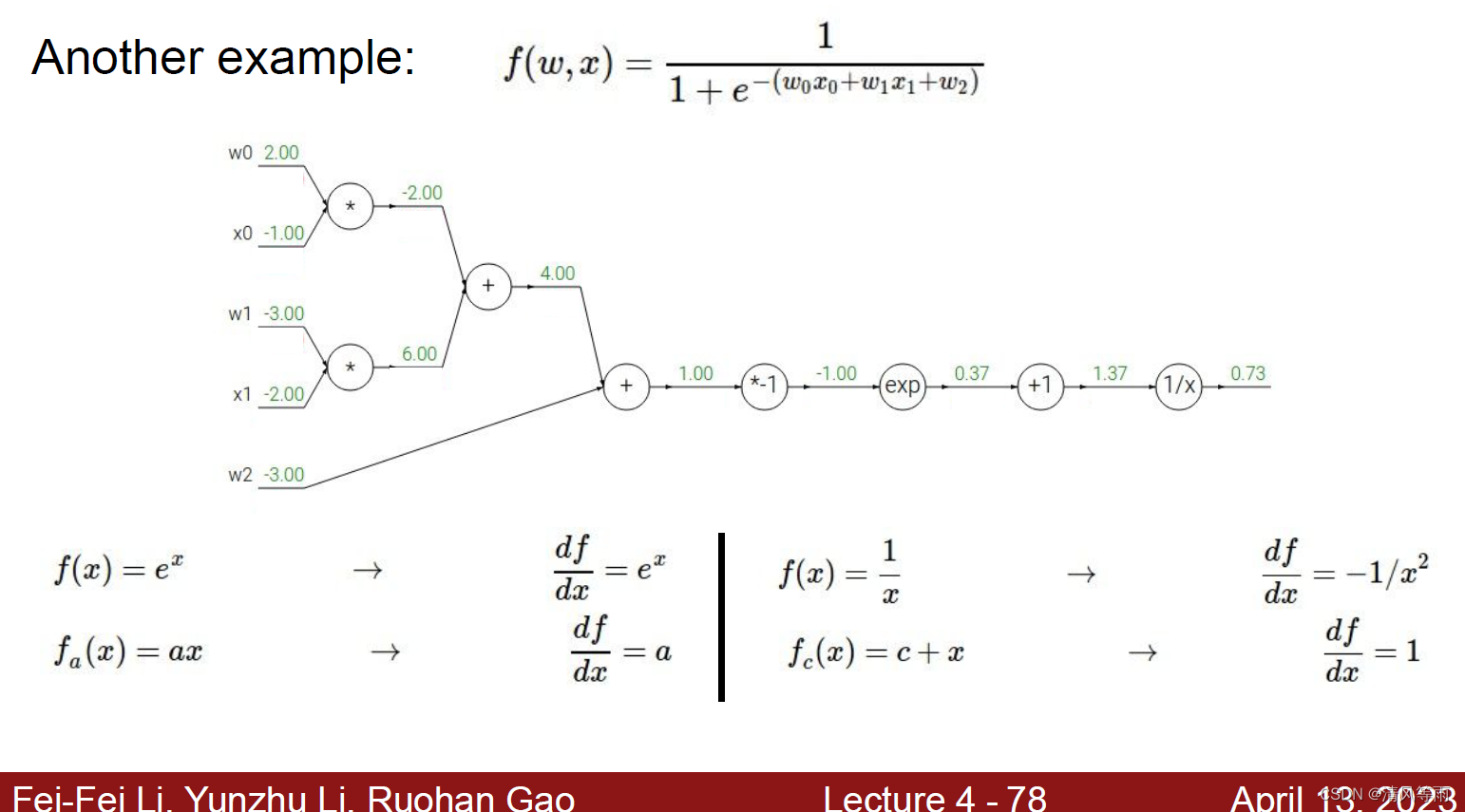
在上面的计算图中，我们知道了它的前向传播的结果以及一些函数的导数，现在，我们来求它的反向传播。过程依然是从后向前，首先我们能求出计算图中的节点1/x处的梯度：

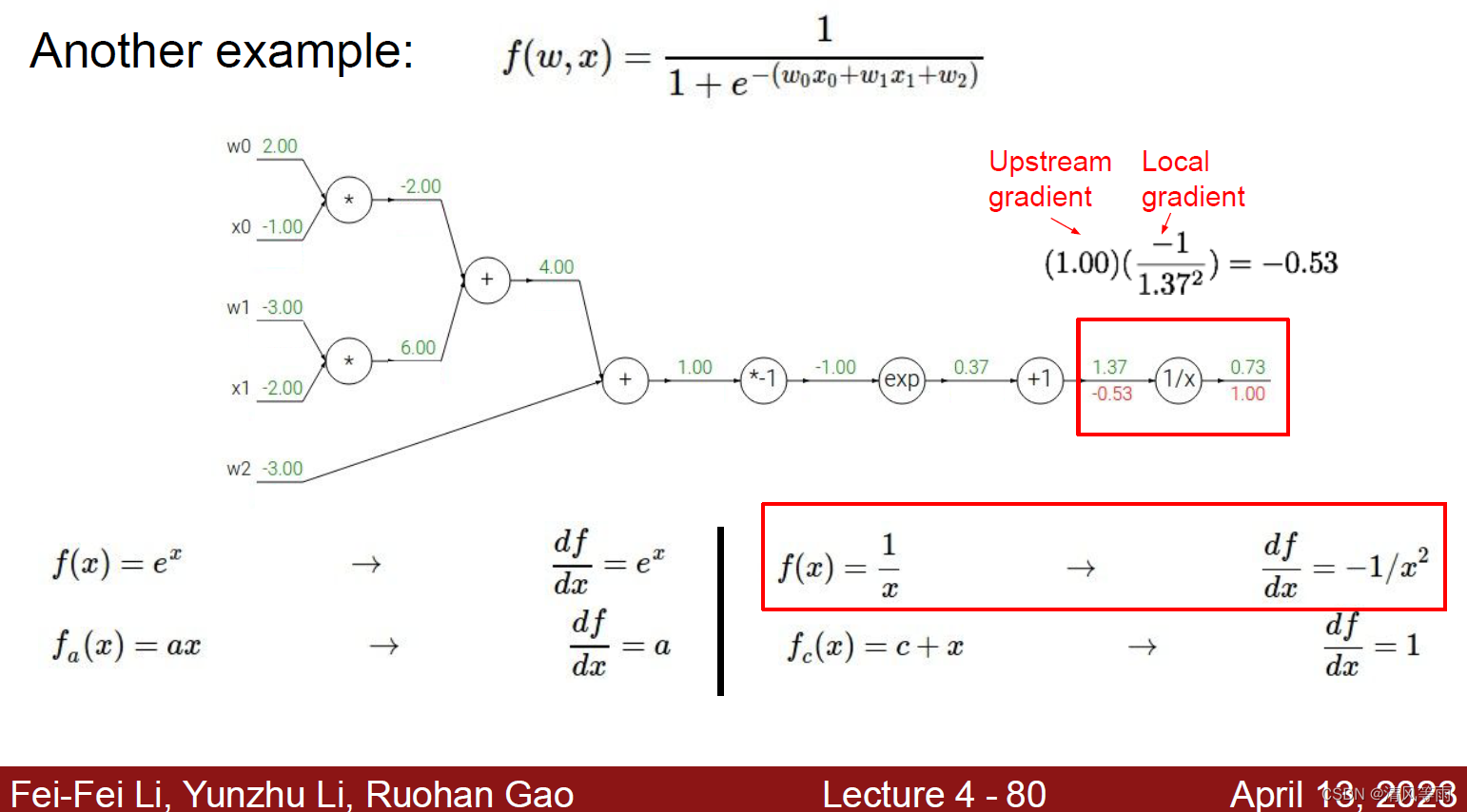
同理，我们可以由后往前地求出计算出中的其他节点梯度：

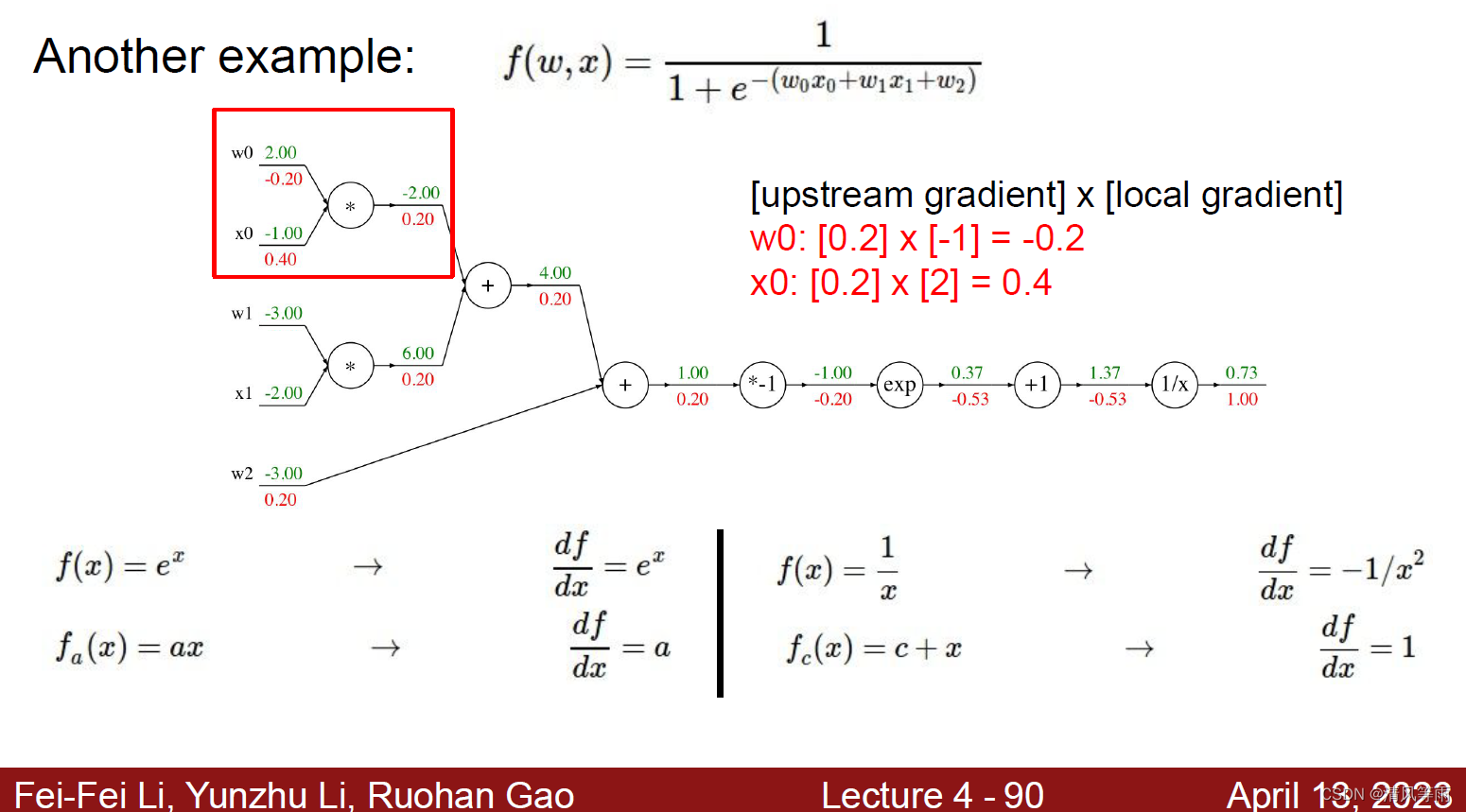
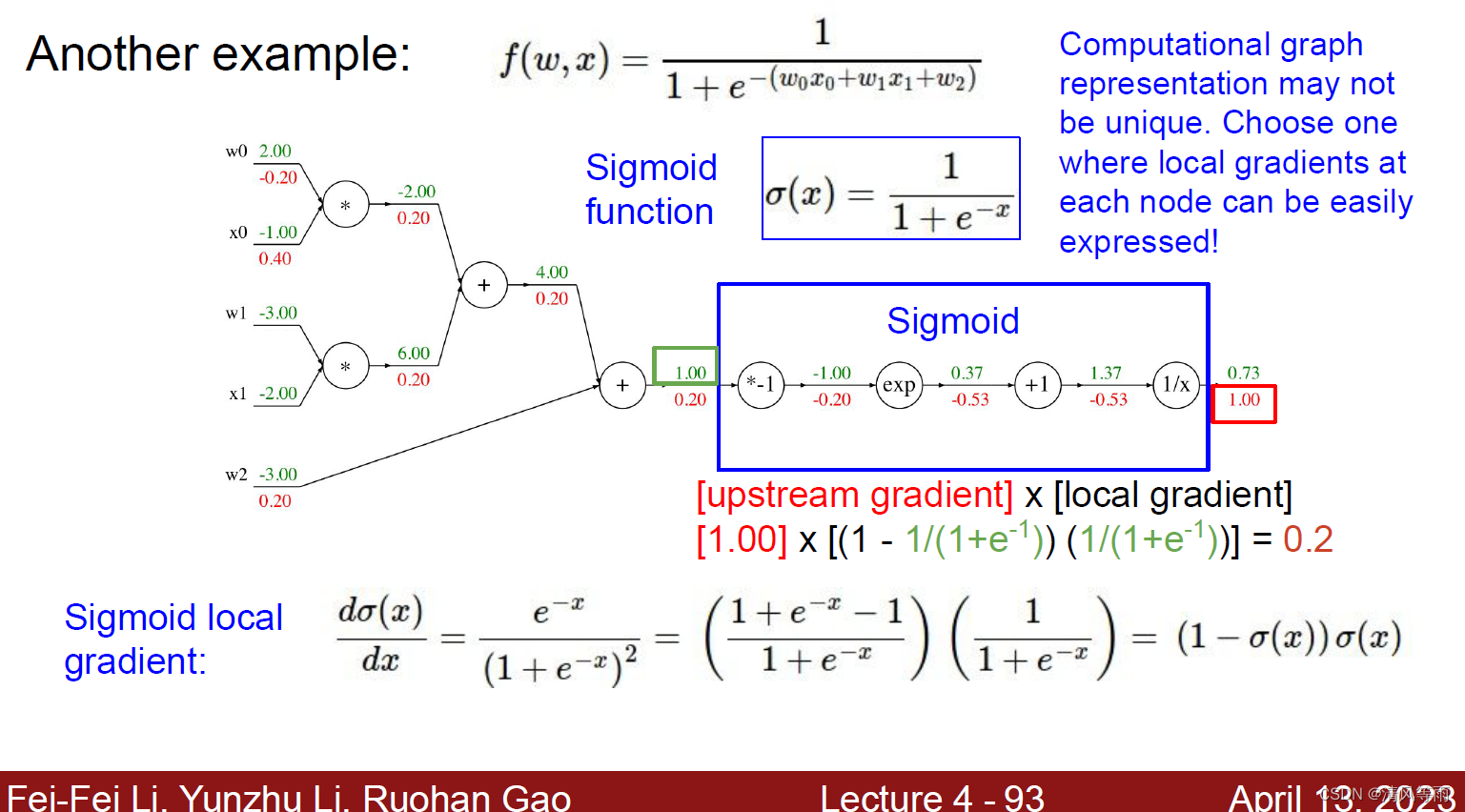
计算图的每个节点代表着每一个操作，因此，计算图的表示可能不唯一。比如说上面的公式中，最后四个节点可以合成一个新的节点(函数sigmoid)。如果将这个函数当作一个节点，那么它的导数以及计算过程如下：


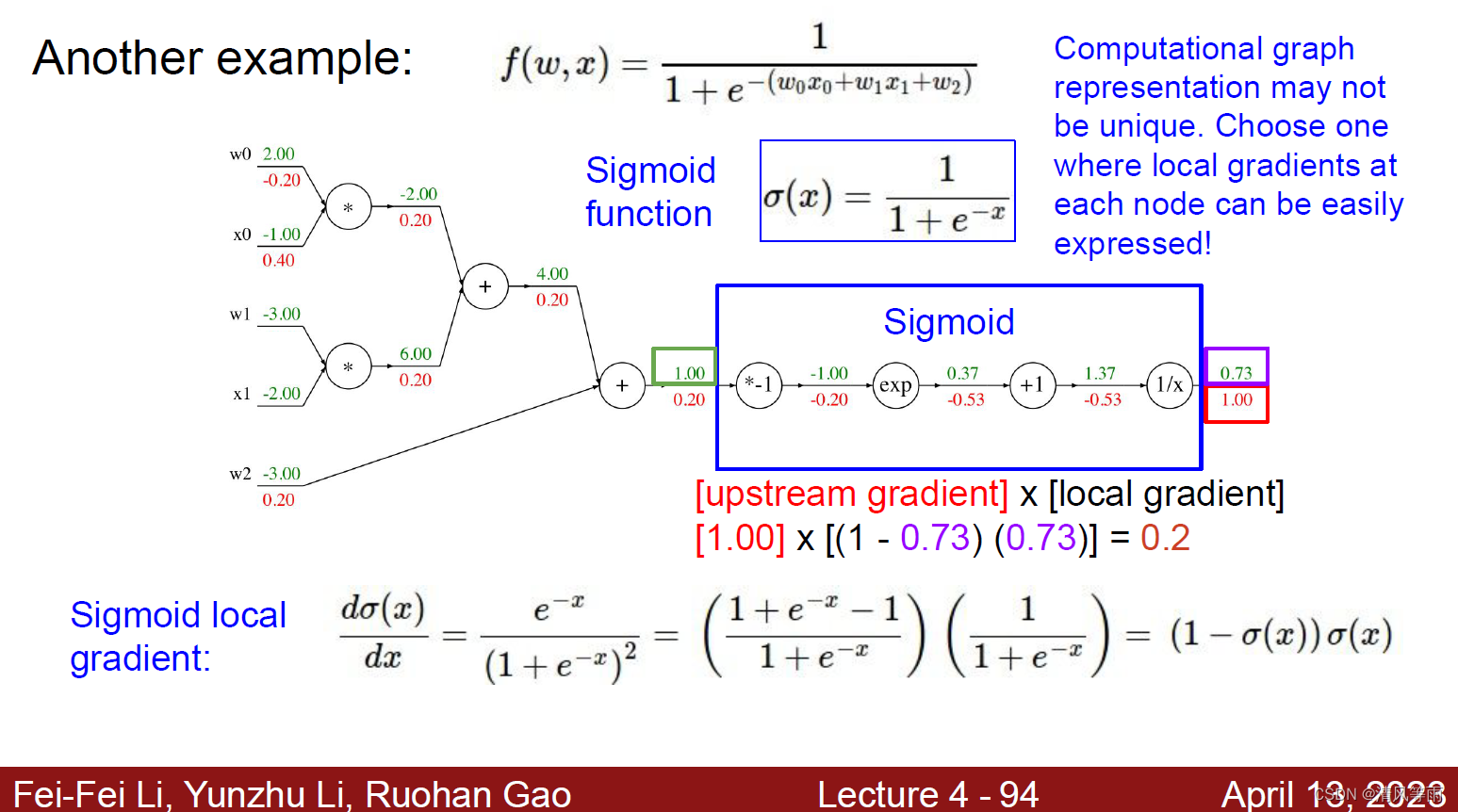
其实现代码为：

def f(w0, w1, w2, x0, x1):
	s0 = w0 * x0
	s1 = w1 * x1
	s2 = s0 + s1
	s3 = s2 * w2
	L = sigmoid(s3) # 假设sigmoid()是已经定义好的sigmoid函数

	grad_L = 1.0
	grad_s3 = grad_L * (1-L) *L
	grad_w2 = grad_s3
	grad_s2 = grad_s3
	grad_s0 = grad_s2
	grad_s1 = grad_s2
	grad_w1 = grad_s1 * w1
	grad_x1 = grad_s1 * w1
	grad_w0 = grad_s0 * w0
	grad_x0 = grad_s0 * w0

或者可以用数组形式来计算:

w = [2,-3,-3] # 输入数据
x = [-1, -2]

# 前向传播
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid函数

# 反向传播
ddot = (1 - f) * f # 点积变量的梯度, 使用sigmoid函数求导
dx = [w[0] * ddot, w[1] * ddot] # 
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] 
# 得到最终输入的梯度

模块化

以上的计算就是反向传播的计算方式，那么将它封装成类(像pytorch的类大体就是这样)，它的代码为：

class ComputationalGraph(object):
	# ...
	def forward(inputs):
		# 1. [把输入放到输入节点...]
		# 2. 计算图中的前向传播:
		for gate in self.graph.nodes_topologically_sorted():
			gate.forward()
		return loss # 计算图中最终输出的损失值
	def backward():
		for gate in reversed(self.graph.nodes_topologically_sorted()):
			gate.backward() # 反向传播(使用链式法则)
		return inputs_gradients	# 输出梯度值	

我们以z = x*y为例，它在PyTorch中的代码为：

class Multiply(torch.autograd.Function):
	@staticmethod
	def forward(ctx, x, y):
		ctx.save_for_backward(×, y) # 需要缓存一些值以便在backward中使用
		z = x * y
		return z
	@staticmethod
	def backward(ctx, grad_z):
		x, y = ctx.saved_tensors
		grad_x= y * grad_z# dz/dx * dL/dz
		grad_y = x * grad_z# dz/dy * dL/dz
		return grad_x, grad_y

向量(或者说矩阵)形式的反向传播

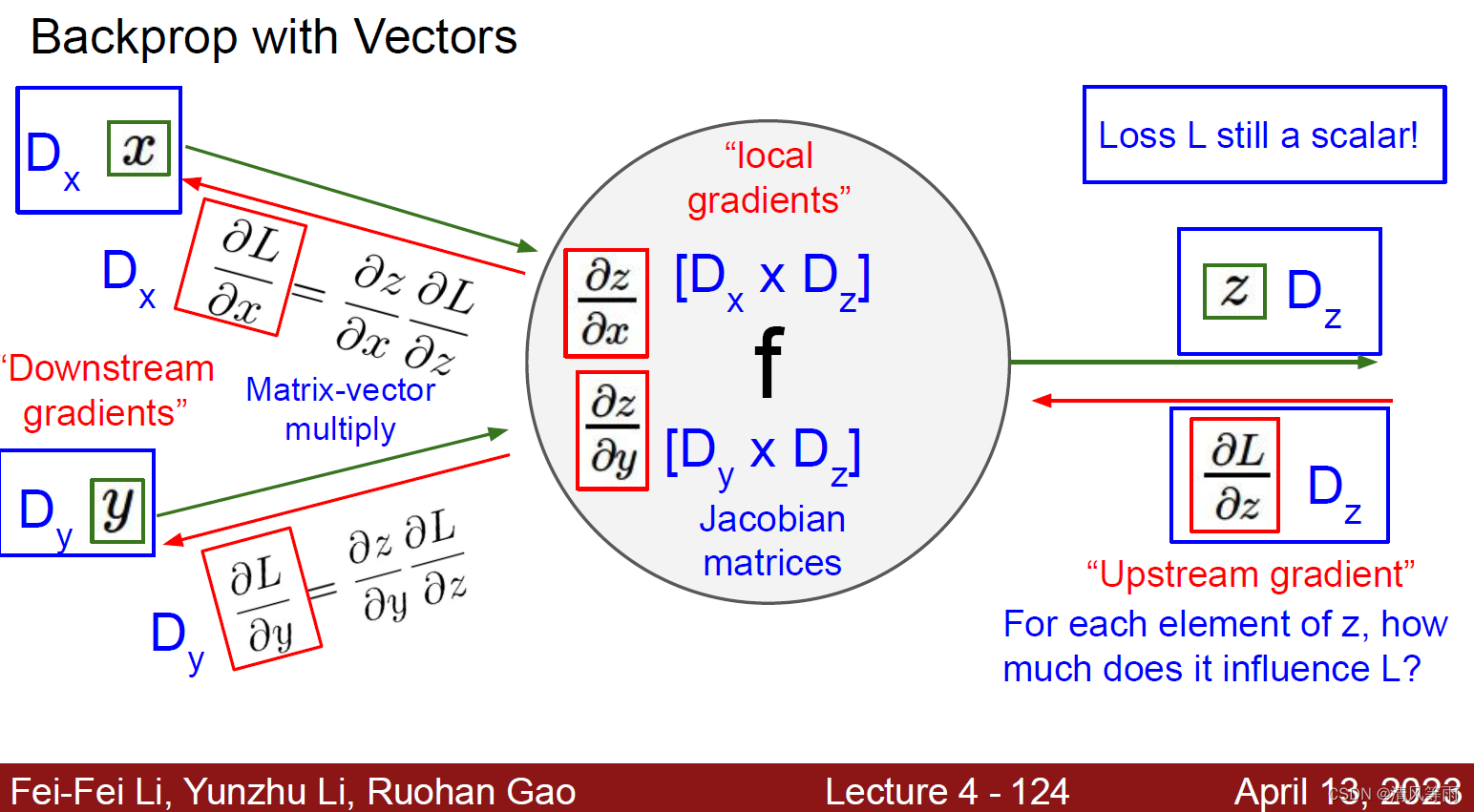
上面我们介绍了输入是标量形式的反向传播，那么如果输入是向量呢(在深度学习中，好像都是向量(或者说矩阵)，至少我没见过标量形式的输入)。其实，向量形式与标量形式差不多，只不过标量的计算都变成了向量(或者说矩阵)的计算，最终得到的值是以雅可比矩阵(Jacobian matrices) (具体可以自行查找关于它的资料)形式展现的。其直观形式如下图：

下面将以输入是向量的形式展示向量形式的反向传播：



如果输入的是一个矩阵(也可以说是一个Tensor)，那么它的反向传播为：

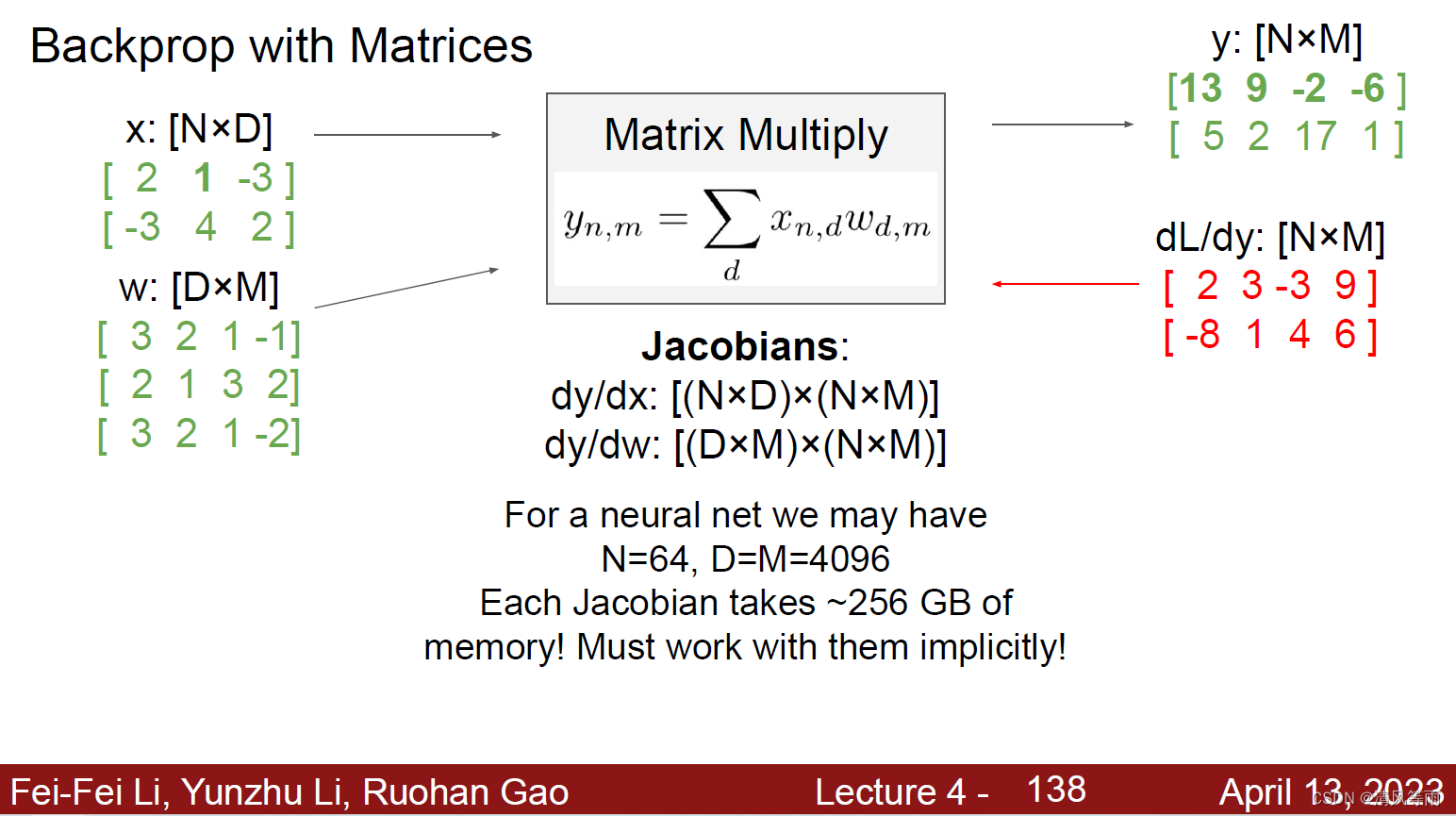
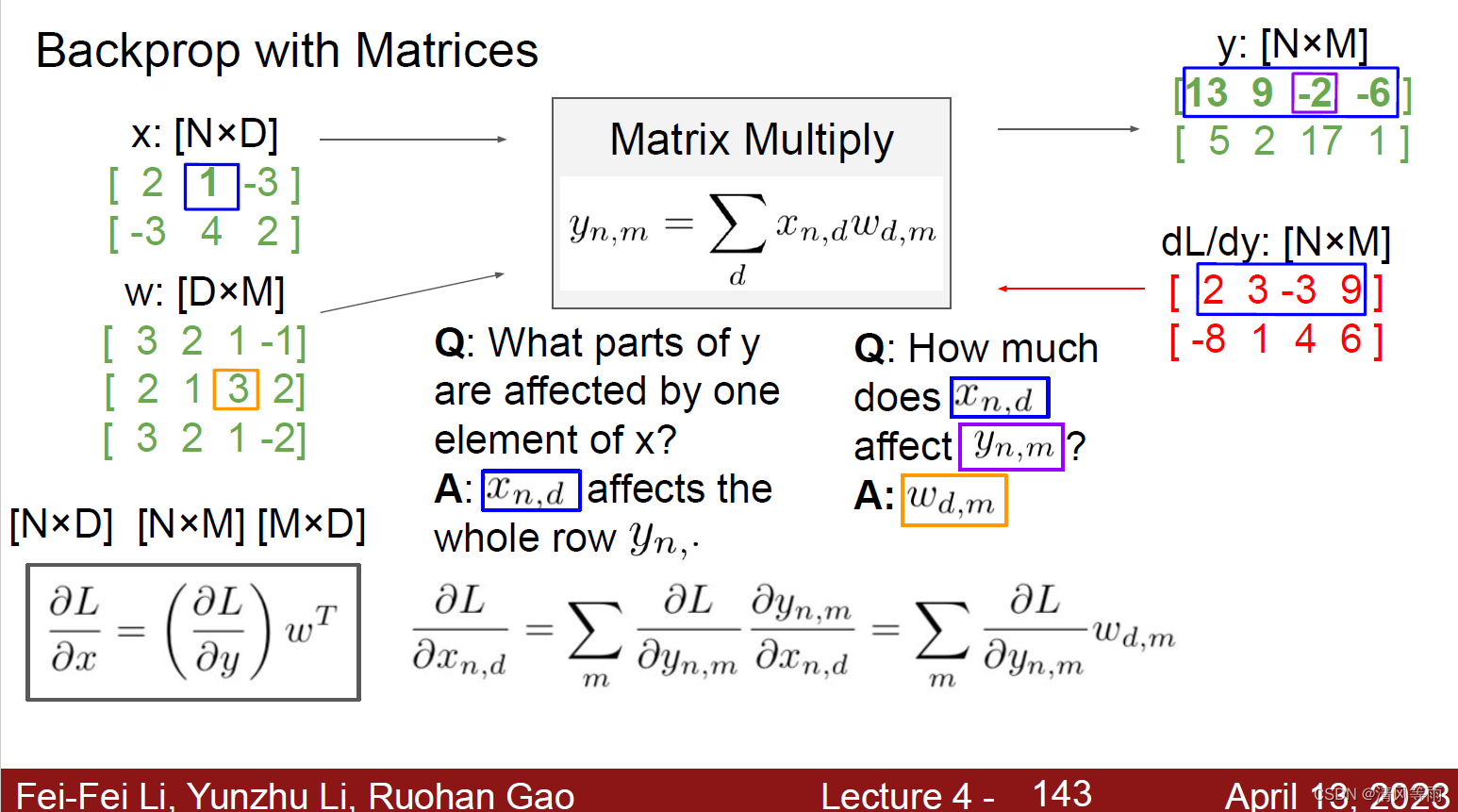
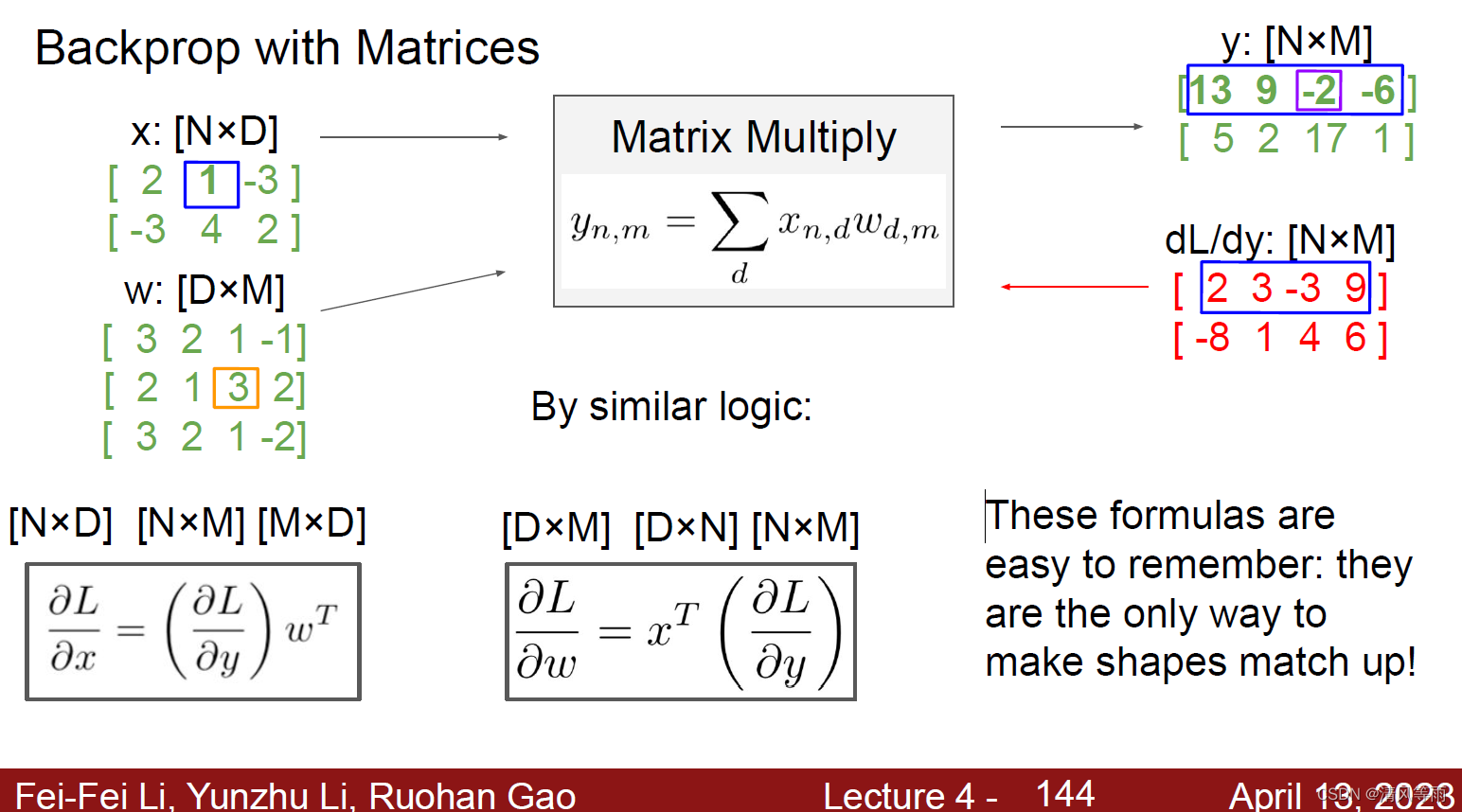
举例

现在，我们来举一个简单的例子(向量形式，矩阵形式是差不多的)来看看具体的反向传播过程。假设有一个公式:$$f(x,W)={\Vert W\cdot x\Vert }^2={\sum }_{i=1}^n(W\cdot x{)}_i^2$$其中x是维度为n的向量，W是形状为n×n的矩阵。设$q=W\cdot x$，于是有$$\left|\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right|$$ $$q=W\cdot x=\left(\begin{array}{c}{W}_{1,1}{x}_1+W_{1,2}{x}_2+\cdots +W_{1,n}{x}_n\\ ⋮\\ W_{n,1}{x}_1+W_{n,2}{x}_2+\cdots +W_{n,n}{x}_n\end{array}\right)$$ $$f(q)={\Vert q\Vert }^2=q_1^2+\cdots +q_n^2$$根据上面得到的公式以及链式求导法则，我们可以得到以下的一些偏导数信息：

1. $\frac{\partial f}{\partial q_i}=2q_i$，所以f对q的梯度为2q。
2. $\frac{\partial q_k}{\partial W_{i,j}}=1_{i=k}{x}_j$, 所以$\frac{\partial f}{\partial W_{i,j}}={\sum }_k\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial W_{i,j}}={\sum }_k(2q_k)(1_{i=k}{x}_j)=2q_i{x}_j$。所以f对W 的梯度为$2q\cdot x^T$。
4. $\frac{\partial q_k}{\partial x_i}=W_{k,i}$, 所以$\frac{\partial f}{\partial x_i}={\sum }_k\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial x_i}={\sum }_k(2q_k)W_{k,i}$。所以f对x 的梯度为$2W^T\cdot q$。

总结

在这篇文章中，我们首先介绍了深度学习目前的一些成果(近两年)，之后讲解了神经网络和反向传播。在神经网络的介绍中，讲解了一些常见的激活函数和神经网络的实现。在反向传播中，通过标量和向量分别的介绍了反向传播的计算。在下一讲中，将开始介绍卷积神经网络。

注

文中所有图片来自于cs231n公开课的网站之中。