文章目录
都会定义损失函数,有了,就可用通过优化算法来尝试最小化损失。
尽管优化提供了一种最大限度地减少深度学习损失函数的方法,但实质上,优化和深度学习的目标是根本不同的。
优化主要关注最小化目标,深度学习关注的是在给定有限数据量的情况下寻找合适的模型。(d2l 4.4小节有讨论)
Hessian矩阵
我们假设函数的输入是维向量,其输出是标量,因此其Hessian矩阵(也称黑塞矩阵)将有k个特征值。函数的解决方案可以是局部最小值、局部最大值或函数梯度为零的位置处的鞍点:
-
当函数在零梯度位置处的Hessian矩阵的特征值全部为正值时,我们有该函数的局部最小值。
-
当函数在零梯度位置处的Hessian矩阵的特征值全部为负值时,我们有该函数的局部最大值。
-
当函数在零梯度位置处的Hessian矩阵的特征值为负值和正值时,我们对函数有一个鞍点。
凸函数是Hessian矩阵的特征值永远不是负值的函数。不幸的是,大多数深度学习问题并不属于这个类别。尽管如此,它还是研究优化算法的一个很好的工具。
1.GD
最朴素的梯度下降,可能由于学习率过大导致优化问题发散;预处理是梯度下降中一种昂常用的技术。
一维中,泰勒展开
f
(
x
+
ϵ
)
=
f
(
x
)
+
ϵ
f
′
(
x
)
+
O
(
ϵ
2
)
f(x + \epsilon) = f(x) + \epsilon f'(x) + O ({\epsilon}^2)
f(x+ϵ)=f(x)+ϵf′(x)+O(ϵ2)
取
ϵ
=
−
η
f
′
(
x
)
\epsilon = -\eta f'(x)
ϵ=−ηf′(x)就得到下面的
f
(
x
−
η
f
′
(
x
)
)
=
f
(
x
)
−
η
f
′
2
(
x
)
+
O
(
η
2
f
′
2
(
x
)
)
.
f(x - \eta f'(x)) = f(x) - \eta f'^2(x) + \mathcal{O}(\eta^2 f'^2(x)).
f(x−ηf′(x))=f(x)−ηf′2(x)+O(η2f′2(x)).
如果
f
′
(
x
)
≠
0
f'(x) \ne 0
f′(x)=0没有消失,就可以继续展开,因为第二项大于零。我们总是可以令
η
\eta
η足够小使得高阶项变得不相关。
因此
f
(
x
−
η
f
′
(
x
)
)
⪅
f
(
x
)
.
f(x - \eta f'(x)) \lessapprox f(x).
f(x−ηf′(x))⪅f(x).
如果我们使用
x
=
x
−
η
f
′
(
x
)
x = x - \eta {f}'(x)
x=x−ηf′(x) 来迭代
x
x
x,函数的值可能会下降
学习率
学习率
η
\eta
η过小,导致
x
x
x的更新过于缓慢,需要更多次迭代才能达到最优值
学习率过大,可能使得高阶项变得显著了。导致发散
局部最小值
考虑函数 f ( x ) = x ⋅ c o s ( x ) f(x) = x·cos(x) f(x)=x⋅cos(x),有无穷多个局部最小值,最终可能最会得到许多解中的一个。

多元梯度下降
∇ f ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , … , ∂ f ( x ) ∂ x d ] ⊤ . \nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top. ∇f(x)=[∂x1∂f(x),∂x2∂f(x),…,∂xd∂f(x)]⊤.
f ( x + ϵ ) = f ( x ) + ϵ ⊤ ∇ f ( x ) + O ( ∥ ϵ ∥ 2 ) . f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \mathbf{\boldsymbol{\epsilon}}^\top \nabla f(\mathbf{x}) + \mathcal{O}(\|\boldsymbol{\epsilon}\|^2). f(x+ϵ)=f(x)+ϵ⊤∇f(x)+O(∥ϵ∥2).
x ← x − η ∇ f ( x ) . \mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x}). x←x−η∇f(x).
自适应方法
自动确定 η \eta η,或者完全不必选择学习率。除了考虑目标函数的值和梯度、还考虑它的曲率的二阶方法可以帮我们解决这个问题。(就是Hessian矩阵),由于计算代价的问题,不能直接应用去深度学习
牛顿法
泰勒展开到更低一级
f
(
x
+
ϵ
)
=
f
(
x
)
+
ϵ
⊤
∇
f
(
x
)
+
1
2
ϵ
⊤
∇
2
f
(
x
)
ϵ
+
O
(
∥
ϵ
∥
3
)
.
f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \boldsymbol{\epsilon}^\top \nabla f(\mathbf{x}) + \frac{1}{2} \boldsymbol{\epsilon}^\top \nabla^2 f(\mathbf{x}) \boldsymbol{\epsilon} + \mathcal{O}(\|\boldsymbol{\epsilon}\|^3).
f(x+ϵ)=f(x)+ϵ⊤∇f(x)+21ϵ⊤∇2f(x)ϵ+O(∥ϵ∥3).
我们将 H = d e f ∇ 2 f ( x ) \mathbf{H} \stackrel{\mathrm{def}}{=} \nabla^2 f(\mathbf{x}) H=def∇2f(x)定义为 f f f的Hessian
毕竟, f f f的最小值满足 ∇ f = 0 \nabla f = 0 ∇f=0。遵循中的微积分规则,通过取 ϵ \boldsymbol{\epsilon} ϵ对上式的导数,再忽略不重要的高阶项,我们便得到
∇
f
(
x
)
+
H
ϵ
=
0
and hence
ϵ
=
−
H
−
1
∇
f
(
x
)
.
\nabla f(\mathbf{x}) + \mathbf{H} \boldsymbol{\epsilon} = 0 \text{ and hence } \boldsymbol{\epsilon} = -\mathbf{H}^{-1} \nabla f(\mathbf{x}).
∇f(x)+Hϵ=0 and hence ϵ=−H−1∇f(x).
需要对Hessian矩阵求逆
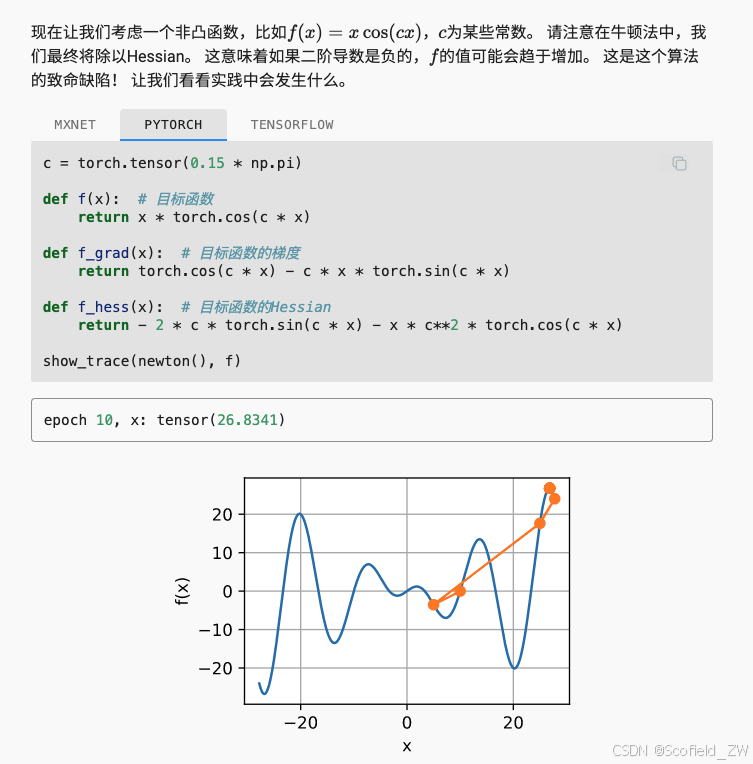
这发生了惊人的错误。我们怎样才能修正它? 一种方法是用取Hessian的绝对值来修正,另一个策略是重新引入学习率。 这似乎违背了初衷,但不完全是——拥有二阶信息可以使我们在曲率较大时保持谨慎,而在目标函数较平坦时则采用较大的学习率。 让我们看看在学习率稍小的情况下它是如何生效的,比如。 如我们所见,我们有了一个相当高效的算法。
ϵ = − η H − 1 ∇ f ( x ) . \boldsymbol{\epsilon} = -\eta \mathbf{H}^{-1} \nabla f(\mathbf{x}). ϵ=−ηH−1∇f(x).

预处理
计算和存储完整的Hessian矩阵代价比较高,预处理就是只计算对角线项?
x ← x − η d i a g ( H ) − 1 ∇ f ( x ) . \mathbf{x} \leftarrow \mathbf{x} - \eta \mathrm{diag}(\mathbf{H})^{-1} \nabla f(\mathbf{x}). x←x−ηdiag(H)−1∇f(x).
梯度下降和线搜索
梯度下降的关键问题是我们可能会超过目标或者进展不足。解决方法之一是使用线搜索和梯度下降。
我们使用
∇
f
(
x
)
\nabla f(\mathbf{x})
∇f(x)给出的方向,
然后进行二分搜索,以确定哪个学习率
η
\eta
η使
f
(
x
−
η
∇
f
(
x
)
)
f(\mathbf{x} - \eta \nabla f(\mathbf{x}))
f(x−η∇f(x))取最小值。
为什么不起作用?
2.随机梯度下降(SGD)
梯度下降为什么不起作用?
随机梯度更新
在深度学习中,目标函数通常是训练数据集中每个样本的损失函数的平均值。给定 n n n个样本的训练数据集,我们假设 f i ( x ) f_i(\mathbf{x}) fi(x)是关于索引 i i i的训练样本的损失函数,其中 x \mathbf{x} x是参数向量。然后我们得到目标函数
f ( x ) = 1 n ∑ i = 1 n f i ( x ) . f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n f_i(\mathbf{x}). f(x)=n1i=1∑nfi(x).
x \mathbf{x} x的目标函数的梯度计算为
∇ f ( x ) = 1 n ∑ i = 1 n ∇ f i ( x ) . \nabla f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}). ∇f(x)=n1i=1∑n∇fi(x).
随机梯度下降可降低每次迭代是的计算代价。在随机梯度下降的每次迭代中,对数据样本随机均匀采样一个索引
i
i
i,其中
i
∈
{
1
,
…
,
n
}
i\in\{1,\ldots, n\}
i∈{1,…,n},并计算梯度
∇
f
i
(
x
)
\nabla f_i(\mathbf{x})
∇fi(x)以更新
x
\mathbf{x}
x:
x
←
x
−
η
∇
f
i
(
x
)
,
\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f_i(\mathbf{x}),
x←x−η∇fi(x),
每次迭代的计算代价从梯度下降的
O
(
n
)
\mathcal{O}(n)
O(n)降至常数
O
(
1
)
\mathcal{O}(1)
O(1)
随机梯度是对完整梯度的无偏估计。
但是因为不确定性,造成这样的情况。

随机梯度下降中变量的轨迹比我们在 :numref:sec_gd中观察到的梯度下降中观察到的轨迹嘈杂得多。这是由于梯度的随机性质。也就是说,即使我们接近最小值,我们仍然受到通过 𝜂∇𝑓𝑖(𝐱) 的瞬间梯度所注入的不确定性的影响。即使经过50次迭代,质量仍然不那么好。更糟糕的是,经过额外的步骤,它不会得到改善。这给我们留下了唯一的选择:改变学习率 𝜂 。但是,如果我们选择的学习率太小,我们一开始就不会取得任何有意义的进展。另一方面,如果我们选择的学习率太大,我们将无法获得一个好的解决方案,如上所示。解决这些相互冲突的目标的唯一方法是在优化过程中动态降低学习率。
这也是在sgd步长函数中添加学习率函数lr的原因。在上面的示例中,学习率调度的任何功能都处于休眠状态,因为我们将相关的lr函数设置为常量。
动态学习率
η ( t ) = η i if t i ≤ t ≤ t i + 1 分段常数 η ( t ) = η 0 ⋅ e − λ t 指数衰减 η ( t ) = η 0 ⋅ ( β t + 1 ) − α 多项式衰减 \begin{aligned} \eta(t) & = \eta_i \text{ if } t_i \leq t \leq t_{i+1} && \text{分段常数} \\ \eta(t) & = \eta_0 \cdot e^{-\lambda t} && \text{指数衰减} \\ \eta(t) & = \eta_0 \cdot (\beta t + 1)^{-\alpha} && \text{多项式衰减} \end{aligned} η(t)η(t)η(t)=ηi if ti≤t≤ti+1=η0⋅e−λt=η0⋅(βt+1)−α分段常数指数衰减多项式衰减
比较常用的是多项式衰减。
随机梯度和有限样本
有替换采样? with replaccment
无替换采样?without repalcement(书里面的选择),就是不对数据样本进行替换,直接选取里面的。
3.小批量随机梯度下降
当数据非常相似的时候,梯度下降并不是非常“数据高效”,CPU与GPU无法充分利用向量化,随梯度下降不是特别搞笑。
折中方案,使用小批量随机梯度下降。————计算效率。
元素相乘——行列相乘——整个矩阵相乘——对矩阵进行分解相乘
从数据集中选择大小为Batch_size个数据样本,在这个样本内部使用梯度下降。
执行更新
w
←
w
−
η
t
g
t
\mathbf{w} \leftarrow \mathbf{w} - \eta_t \mathbf{g}_t
w←w−ηtgt,其中
g
t
=
∂
w
f
(
x
t
,
w
)
.
\mathbf{g}_t = \partial_{\mathbf{w}} f(\mathbf{x}_{t}, \mathbf{w}).
gt=∂wf(xt,w).
小批量中
g
t
\mathbf{g}_t
gt,
g
t
=
∂
w
1
∣
B
t
∣
∑
i
∈
B
t
f
(
x
i
,
w
)
.
\mathbf{g}_t = \partial_{\mathbf{w}} \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} f(\mathbf{x}_{i}, \mathbf{w}).
gt=∂w∣Bt∣1∑i∈Btf(xi,w).
in pytorch tensor.backward()计算梯度,optimizer.step()更新参数。
4.动量法
无噪声梯度下降和有噪声梯度下降?
平均梯度减小了方差。
泄漏平均值(leaky average)
算法
v t = β v t − 1 + g t , t − 1 \mathbf{v}_t = \beta \mathbf{v}_{t-1} + \mathbf{g}_{t, t-1} vt=βvt−1+gt,t−1
v t = β 2 v t − 2 + β g t − 1 , t − 2 + g t , t − 1 = … , = ∑ τ = 0 t − 1 β τ g t − τ , t − τ − 1 . \begin{aligned} \mathbf{v}_t = \beta^2 \mathbf{v}_{t-2} + \beta \mathbf{g}_{t-1, t-2} + \mathbf{g}_{t, t-1} = \ldots, = \sum_{\tau = 0}^{t-1} \beta^{\tau} \mathbf{g}_{t-\tau, t-\tau-1}. \end{aligned} vt=β2vt−2+βgt−1,t−2+gt,t−1=…,=τ=0∑t−1βτgt−τ,t−τ−1.
x t ← x t − 1 − η t v t . \begin{aligned} \mathbf{x}_t &\leftarrow \mathbf{x}_{t-1} - \eta_t \mathbf{v}_t. \end{aligned} xt←xt−1−ηtvt.
需要一组辅助变量来记录速度 v t \mathbf{v}_t vt
5.AdaGrad算法
训练语言模型——稀疏特征的模型训练。只有在这些不常见特征出现时,与其相关的参数才会得到有意义的更新。
学习率:对于常见特征来说降低的太慢,对于不常见特征来说下降的太快。——想到可以用记录特征出现的次数,然后调整学习率。即使用
η
i
=
η
0
s
(
i
,
t
)
+
c
\eta_i = \frac{\eta_0}{\sqrt{s(i, t) + c}}
ηi=s(i,t)+cη0的学习率,而不是
η
=
η
0
t
+
c
\eta = \frac{\eta_0}{\sqrt{t + c}}
η=t+cη0,
s
(
i
,
t
)
s(i, t)
s(i,t)计下了我们截至
t
t
t 时观察到特征
i
i
i的次数。
AdaGrad算法通过将计数器替换为先前观测所得到的梯度平方之和,即
s
(
i
,
t
+
1
)
=
s
(
i
,
t
)
+
(
∂
i
f
(
x
)
)
2
s(i, t+1) = s(i, t) + \left(\partial_i f(\mathbf{x})\right)^2
s(i,t+1)=s(i,t)+(∂if(x))2。
两个好处
- 不再需要决定梯度何时算足够大。
- 会随着梯度的大小自动变化。
AdaGrad中使用了一个代理来表示Hessian矩阵
算法
g t = ∂ w l ( y t , f ( x t , w ) ) , s t = s t − 1 + g t 2 , w t = w t − 1 − η s t + ϵ ⋅ g t . \begin{aligned} \mathbf{g}_t & = \partial_{\mathbf{w}} l(y_t, f(\mathbf{x}_t, \mathbf{w})), \\ \mathbf{s}_t & = \mathbf{s}_{t-1} + \mathbf{g}_t^2, \\ \mathbf{w}_t & = \mathbf{w}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \cdot \mathbf{g}_t. \end{aligned} gtstwt=∂wl(yt,f(xt,w)),=st−1+gt2,=wt−1−st+ϵη⋅gt.
6.RMSProp算法
坐标自适应是什么?——我的理解是每一个参数都有其对应的计算?主要是在
s
t
−
1
与
s_{t-1}与
st−1与
g
t
2
g_t^2
gt2中,是一一对应的。
将速率调度与坐标自适应分离?
AdaGrad算法中中的
S
t
S_t
St的更新缺乏规范化,没有约束力,
S
t
S_t
St持续增长,是持续递增的。
- 解决1.使用 S t t \frac{S_t}{t} tSt,是合理的,可以收敛。但是生效时间可能会很长。
- 使用泄漏平均值。 s t ← γ s t − 1 + ( 1 − γ ) g t 2 \mathbf{s}_t \leftarrow \gamma \mathbf{s}_{t-1} + (1-\gamma) \mathbf{g}_t^2 st←γst−1+(1−γ)gt2
算法
s
t
←
γ
s
t
−
1
+
(
1
−
γ
)
g
t
2
,
x
t
←
x
t
−
1
−
η
s
t
+
ϵ
⊙
g
t
.
\begin{aligned} \mathbf{s}_t & \leftarrow \gamma \mathbf{s}_{t-1} + (1 - \gamma) \mathbf{g}_t^2, \\ \mathbf{x}_t & \leftarrow \mathbf{x}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \odot \mathbf{g}_t. \end{aligned}
stxt←γst−1+(1−γ)gt2,←xt−1−st+ϵη⊙gt.
常数
ϵ
>
0
\epsilon > 0
ϵ>0通常设置为
1
0
−
6
10^{-6}
10−6
7.Adadelta
是Adagrad的一种变体:主要区别是减少了学习率适应坐标的数量。
没有学习率?从公式中就可以看出来
算法
s t = ρ s t − 1 + ( 1 − ρ ) g t 2 . \begin{aligned} \mathbf{s}_t & = \rho \mathbf{s}_{t-1} + (1 - \rho) \mathbf{g}_t^2. \end{aligned} st=ρst−1+(1−ρ)gt2.
g
t
′
=
Δ
x
t
−
1
+
ϵ
s
t
+
ϵ
⊙
g
t
,
\begin{aligned} \mathbf{g}_t' & = \frac{\sqrt{\Delta\mathbf{x}_{t-1} + \epsilon}}{\sqrt{{\mathbf{s}_t + \epsilon}}} \odot \mathbf{g}_t, \\ \end{aligned}
gt′=st+ϵΔxt−1+ϵ⊙gt,
它使用参数本身的变化率来调整学习率。
x
t
=
x
t
−
1
−
g
t
′
.
\begin{aligned} \mathbf{x}_t & = \mathbf{x}_{t-1} - \mathbf{g}_t'. \\ \end{aligned}
xt=xt−1−gt′.
Δ
x
t
=
ρ
Δ
x
t
−
1
+
(
1
−
ρ
)
g
t
′
2
,
\begin{aligned} \Delta \mathbf{x}_t & = \rho \Delta\mathbf{x}_{t-1} + (1 - \rho) {\mathbf{g}_t'}^2, \end{aligned}
Δxt=ρΔxt−1+(1−ρ)gt′2,
其中
Δ
x
0
\Delta \mathbf{x}_0
Δx0初始化为零。
需要记录 s t \mathbf{s}_t st和 Δ x t \Delta\mathbf{x}_t Δxt。上面公式的顺序就是参数计算的顺序。
8.Adam算法
- SGD解决优化问题比梯度下降更有效。
- mini-batch中,在一个小批量中使用更大的观测值集,可以通过项量化提供额外的效率。并行处理
- 动量法中:添加了一种机制使得可以利用过去的梯度以加速收敛。
- AdaGrad:处理稀疏特征值的时候,学习力的问题,通过对每个坐标(参数的学习率)实行缩放
- RMSProp,通过学习率的调整来分离每个坐标的缩放(泄漏平均值)
- Adam:将所有技术汇总到一起。
算法
使用指数加权平均移动值来估计梯度的动量和二次矩。
v
t
←
β
1
v
t
−
1
+
(
1
−
β
1
)
g
t
,
s
t
←
β
2
s
t
−
1
+
(
1
−
β
2
)
g
t
2
.
\begin{aligned} \mathbf{v}_t & \leftarrow \beta_1 \mathbf{v}_{t-1} + (1 - \beta_1) \mathbf{g}_t, \\ \mathbf{s}_t & \leftarrow \beta_2 \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2. \end{aligned}
vtst←β1vt−1+(1−β1)gt,←β2st−1+(1−β2)gt2.
为什么要改成下面这样,因为如果s,v初始化为零的时候,初始偏差就会比较大
v ^ t = v t 1 − β 1 t and s ^ t = s t 1 − β 2 t . \hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_1^t} \text{ and } \hat{\mathbf{s}}_t = \frac{\mathbf{s}_t}{1 - \beta_2^t}. v^t=1−β1tvt and s^t=1−β2tst.
g t ′ = η v ^ t s ^ t + ϵ . \mathbf{g}_t' = \frac{\eta \hat{\mathbf{v}}_t}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon}. gt′=s^t+ϵηv^t.
x t ← x t − 1 − g t ′ . \mathbf{x}_t \leftarrow \mathbf{x}_{t-1} - \mathbf{g}_t'. xt←xt−1−gt′.
动量和规模都在里面了。
问题与改进 Yogi
即使在凸环境下,当
s
t
\mathbf{s}_t
st的二次矩估计值爆炸时,它可能无法收敛。
建议改成
s
t
←
s
t
−
1
+
(
1
−
β
2
)
(
g
t
2
−
s
t
−
1
)
.
\mathbf{s}_t \leftarrow \mathbf{s}_{t-1} + (1 - \beta_2) \left(\mathbf{g}_t^2 - \mathbf{s}_{t-1}\right).
st←st−1+(1−β2)(gt2−st−1).
g太大s会很快忘记过去,改成下面
s
t
←
s
t
−
1
+
(
1
−
β
2
)
g
t
2
⊙
s
g
n
(
g
t
2
−
s
t
−
1
)
.
\mathbf{s}_t \leftarrow \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2 \odot \mathop{\mathrm{sgn}}(\mathbf{g}_t^2 - \mathbf{s}_{t-1}).
st←st−1+(1−β2)gt2⊙sgn(gt2−st−1).
还建议使用更大初始batch
学习率调度器
前面关心的都是怎么更新权重,不是更新的速率,学习率更新的速率也重要。
学习率本身也可以进行更新。
降低学习率可以减少过拟合。
- 大小问题。
- 衰减速率问题。
- 初始化问题——warmup——防止发散
- 还可以周期性质调整学习率
AdamW

v t ← β 1 v t − 1 + ( 1 − β 1 ) g t , s t ← β 2 s t − 1 + ( 1 − β 2 ) g t 2 . \begin{aligned} \mathbf{v}_t & \leftarrow \beta_1 \mathbf{v}_{t-1} + (1 - \beta_1) \mathbf{g}_t, \\ \mathbf{s}_t & \leftarrow \beta_2 \mathbf{s}_{t-1} + (1 - \beta_2) \mathbf{g}_t^2. \end{aligned} vtst←β1vt−1+(1−β1)gt,←β2st−1+(1−β2)gt2.
v ^ t = v t 1 − β 1 t and s ^ t = s t 1 − β 2 t . \hat{\mathbf{v}}_t = \frac{\mathbf{v}_t}{1 - \beta_1^t} \text{ and } \hat{\mathbf{s}}_t = \frac{\mathbf{s}_t}{1 - \beta_2^t}. v^t=1−β1tvt and s^t=1−β2tst.
x t ← x t − 1 − η t ( α v ^ t s ^ t + ϵ + λ x t − 1 ) . \mathbf{x}_t \leftarrow \mathbf{x}_{t-1} - \eta_t(\frac{\alpha\hat{\mathbf{v}}_t}{\sqrt{\hat{\mathbf{s}}_t} + \epsilon} + \lambda \mathbf{x}_{t-1}). xt←xt−1−ηt(s^t+ϵαv^t+λxt−1).
LABM
其中,
ϕ
\phi
ϕ 是一个可选择的映射函数,一种是
ϕ
(
z
)
=
z
\phi(z)=z
ϕ(z)=z,另一种则为起到归一化作用的
ϕ
(
z
)
=
min
(
max
(
z
,
γ
l
)
,
γ
u
)
\phi (z) = \min (\max(z, \gamma_l),\gamma_u)
ϕ(z)=min(max(z,γl),γu) ,
γ
l
\gamma_l
γl and
γ
u
\gamma_u
γu is the lower and upper bound
adamw的时候batchsize超过512模型效果就下降了
batch size 可以到32,000
























 1028
1028

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








