Dijkstra算法详解

算法简介

• 用于计算从一个顶点到其余各顶点的最短路径算法
• 适用于权值为非负的图的单源最短路径，用斐波那契堆的复杂度O(E+VlgV)
• 主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止

算法思想

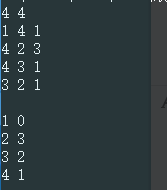
这里我们以这组例子为列

1 4 1
4 2 3
4 3 1
3 2 1

在这里我们使用数组vis数组来标记未走过的节点

以dis数组来存储从 1 到 到 1 2 3 4 每个点的最短路径

代码实现:

import java.util.*;
import java.io.*;
public class Dijkstra {
    private static final int  MAX = 1 << 29;//两点间没有距离 则设为最大值
    private static Scanner scanner ;
    private static int[][] map ;
    private static int[] dis ,vis;
    private static int num ,mum;
    static {
        map = new int[100][100];
        dis = new int[100];//记录最短路径
        vis = new int[100];//标记被走过的点
        scanner = new Scanner(new BufferedInputStream(System.in));
    }
    public static void main(String[] args) {
        while(scanner.hasNext()) {
            num = scanner.nextInt();
            mum = scanner.nextInt();
            /*初始化邻接矩阵 */
            for (int i = 1 ; i<=num ; i++) {
                for (int j = 1; j<= num ; j++) {
                    if (i!=j) {
                        map[i][j] = MAX;
                    }else {
                        map[i][j] = 0;
                    }
                }
            }
            /*初始化两点距离*/
            for (int i = 1; i<=mum; i++ ) {
                int x,y,z;
                x = scanner.nextInt();
                y = scanner.nextInt();
                z = scanner.nextInt();
                map[x][y] = z;
            }

            dij(1);
            System.out.println();
            for (int i = 1;  i<=num; i++) {
                System.out.printf("%d %d\n",i,dis[i]);
            }
        }
    }

    private static void dij(int s) {
        for (int i = 1; i<=num ;i++ ) {
            /*初始化起点未走过 */
            vis[i] = 0;
            /*初始化 dis数组*/
            dis[i] = map[s][i];

        }
        /*标记起点已被走过*/
        vis[s] = 1;
        dis[s] = 0;
        /* 遍历所有的顶点*/
        for (int i = 1;i<=num ; i++) {
            /*to 用于记住满足条件的点的下标*/
            int to = 1;
            int d = MAX;
            for (int j = 1; j<=num ; j++) {
                /*满足此顶点未被走过 且 此顶点没有权值(未表明距离)*/
                if (vis[j]==0 && d > dis[j]) {
                    d = dis[j];
                    to = j;
                }
            } 
            /* 标记此点被走过*/
            vis[to] = 1;
            for (int j = 1;j<=num ;j++) {
                /* 获得当前最短路径存入dis数组*/
                if (vis[j]==0 && dis[j] > dis[to]+map[to][j]) {
                    dis[j] = dis[to] + map[to][j];
                }
            }
        }
    }
}

* 现在我们来分析dij函数，首先我们初始化了dis数组与vis数组，然后标记了第一个点，进入for循环来遍历每个点，然后在第二层for循环中找到未被走过的点，然后对其进行标记，然后通过一个for循环来找到当前点与其他点的最短路径然后记录在dis数组中*

* 这里的结果就是从 1 到 1 2 3 4 的每个的最短距离了*