机器学习十大算法之SVM

最新推荐文章于 2024-09-01 19:21:12 发布

zlinxi

最新推荐文章于 2024-09-01 19:21:12 发布

阅读量572

点赞数

分类专栏：机器学习文章标签：分类 SVM 机器学习

机器学习专栏收录该内容

12 篇文章 5 订阅

订阅专栏

一、概述

支持向量机（SVM）是一种二类分类模型，属于监督学习的方法，广泛用于统计分类以及回归分析。它是在特征空间上的间隔最大的线性分类器，支持向量机还包括核技巧，从而使该模型可以使用于非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。

二、算法原理

1、线性分类器

这里我们需要了解一个很重要的分类标准，Logistic回归。

给定一些数据点，分别属于两个不同的类别，现在需要一个线性分类器将这些数据点分成两类。这里x表示数据点，y表示分类标签（1或0代表两个类别），我们需要找到一个超平面将数据点分成两类，将超平面的方程表示为： $w^{T}x+b=0$ ，接下来我们就需要用到Logistic回归模型（称为Sigmoid函数）将自变量映射到（0,1）上，这里函数表示为： $h_{\theta }(x)=g(\theta ^{T}x)=1/(1+e^{-\theta ^{T}x})$ ，即为logistic函数，如下图像：

è¿éåå¾çæè¿°

可以看出，sigmoid函数连续，光滑，严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。当x趋近负无穷时，y趋近于0；趋近于正无穷时，y趋近于1；x=0时，y=0.5。于是有如下公式：

当我们要判别一个新来的特征属于哪个类时，只需求即可，若大于0.5就是y=1的类，反之属于y=0类。Logistic回归就是要学习得到，使得正例的特征远大于0，负例的特征远小于0，而且要在全部训练实例上达到这个目标。

接下来，尝试把logistic回归做个变形。首先，将使用的结果标签y = 0和y = 1替换为y = -1,y = 1，然后将（）中的替换为b，最后将后面的替换为（即）。如此，则有了。也就是说除了y由y=0变为y=-1外，线性分类函数跟logistic回归的形式化表示没区别。进一步，可以将假设函数中的g(z)做一个简化，将其简单映射到y=-1和y=1上。映射关系如下：

因此，我们可以利用sigmoid函数作为SVM分类的分类器。

2、最大间隔的引出

知道了线性分类器，下面我们举一个线性分类的例子来说明SVM间隔最大化的原理。如下图，在一个二维平面中，有红蓝两种不同的点，为不同的两个类别，红色直线为一个可行的超平面。

从上图中可以看出超平面将不同颜色的两种数据点分开，超平面一边数据点对应的y为-1，另一边的y为1。接着我们定义分类函数为 $f(x)=w^{T}x+b$ ，由此可以得到如下图形：

注：上图中，定义特征到结果的输出函数 u = w· ⃗x − b，与我们之前定义的f(x) = wT x + b 实质是一样的，不影响最终的优化结果。

这里位于wx + b = 1与wx + b = -1的直线上的点就是支持向量我们在前面乘上一个该点所属的类别y（y=1或-1），就可以得到支持向量的表达式为：y(wx + b) = 1，这样就可以更简单的将支持向量表示出来了，这样支持向量后面的点就不用参与计算了。因此，我们就要确定分类函数的两个参数w和b。如何求w和b呢？这里我们寻找两条边界端或极端划分直线中间的最大间隔，从而确定最终的最大间隔分类超平面 hyper plane 和分类函数，进而把寻求分类函数 f(x) = w · x + b 的问题转化为对 w，b 的最优化问题，最终化为对偶因子的求解。即从最大间隔出发（目的本就是为了确定法向量 w），转化为求对变量 w 和 b 的凸二次规划问题。

通过几何学的知识，我们知道点到超平面 $(\beta, \beta_{0})$ 的距离为:

特别的，对于超平面, 表达式中的分子为1，因此支持向量到超平面的距离是: $\gamma =1/\left \| w \right \|$

接下来，给出优化求解的表达式：

||w||的意思是w的二范数，最大化这个式子等价于最小化||w||, 另外由于||w||是一个单调函数，我们可以对其加入平方，这个式子是为了方便求导。这个式子有还有一些限制条件，完整的写下来，应该是这样的：

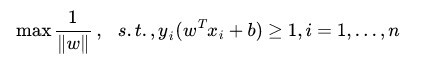
3、拉格朗日优化

通过上面的分析，我们得到了目标函数，要求解该式子，我们可以通过求对偶问题得到最优解。这里我们将优化问题用拉格朗日乘子法求解，使用KKT（Karush–Kuhn–Tucker conditions）理论，这里给出拉格朗日目标函数：

这里让L关于w和b最小化，分别令L关于w，b的偏导数为0，得到如下表达式：

代入原式得：

加上限制条件，对 $\alpha$ 最大化，得到如下式子：

容易验证，当某个约束条件不满足时，例如，那么显然有（只要令即可）。而当所有约束条件都满足时，则最优值为，亦即最初要最小化的量。因此，在要求约束条件得到满足的情况下最小化，实际上等价于直接最小化（当然，这里也有约束条件，就是≥0,i=1,…,n），因为如果约束条件没有得到满足，会等于无穷大，自然不会是我们所要求的最小值。具体写出来，目标函数变成了：，这样就得到了线性可分问题的优化式子。