规模为n的问题通过分治,得到a个规模为n/b的问题,每次递归带来的额外计算为c(n^d)
T(n) <= aT(n/b)+c(n^d)
那么就可以得到问题的复杂度为:
T(n) = O(n^d log(n)), if a = b^d
T(n) = O(n^d ), if a < b^d
T(n) = O(n^logb(a))), if a > b^d
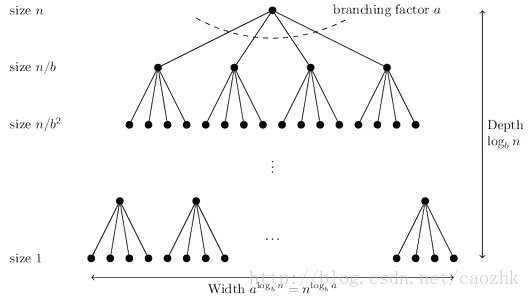
可见,每次递归把问题分为a个规模为n/b的子问题。从根节点开始,共有logb(n)+1层,叶子节点数为a(logb(n))。那么,第j层共有aj个子问题,每个问题规模为n/bj,每个子问题运算量为c*(n/bj)^d需要完成的计算量为:
求和得到整个问题的运算量:
那么,根据a与b^d的关系,很容易得到主定理。
应用
二分搜索
每次问题规模减半,a=1,b=2,d=0
复杂度为n^0 log(n) = log(n)。
快速排序
随机选择待排序序列中的一个数字作为划分字问题的标准,划分是否平均影响算法复杂度
每次问题规模减半,a=2,b=2,d=1
复杂度为n^2 log(n)
最差情况下,复杂度为O(n^2)
归并排序
数据列均分为两部分,分别排序,之后以O(n)的复杂度进行合并,空间复杂度O(n)
每次问题规模减半,a=2,b=2,d=1
复杂度为n log(n)
基数排序(Radix sort)
对于待排序的整数序列,从最低位到最高位每次按照相应的位排序一次
每次递归问题规模变为原来的1/10,但需要求解10个子问题,额外运算为O(n)的,a=10,b=10,d=1
复杂度为n^1 log(n) = n log(n),近似为O(kN),k为整数的位数
快速傅里叶变换:FFT
每次问题规模减半,a=2,b=2,d=1
复杂度为n log(n)
Karatsuba快速乘法
正常两个n位数乘法为n^2
算法把两个乘数各分为高低位两部分,如X*Y = (a+b) * (c+d) = ac+bd + (bc+ad) = ac+bd+(ac+bd - (a-b)(c-d))
只需要ac,bd,(a-b)(c-d)三次乘法
每次问题规模减半,但需要解3个子问题,加法是O(n)的,a=3,b=2,d=1
复杂度为n^log2(3)







 本文探讨了使用分治策略解决问题时的算法复杂度分析,特别是通过主定理推导出的时间复杂度。当问题规模为n,分成a个规模为n/b的子问题,额外计算量为c(n^d)时,根据a与b^d的关系,复杂度可表示为:T(n) = O(n^d log(n))、O(n^d)或O(n^logb(a))。主定理广泛应用于二分搜索、快速排序、归并排序、基数排序和快速傅里叶变换等算法中。
本文探讨了使用分治策略解决问题时的算法复杂度分析,特别是通过主定理推导出的时间复杂度。当问题规模为n,分成a个规模为n/b的子问题,额外计算量为c(n^d)时,根据a与b^d的关系,复杂度可表示为:T(n) = O(n^d log(n))、O(n^d)或O(n^logb(a))。主定理广泛应用于二分搜索、快速排序、归并排序、基数排序和快速傅里叶变换等算法中。

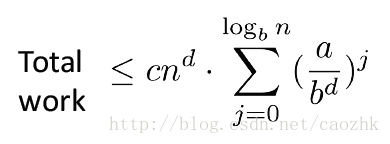














 639
639

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








