现代计算机图形学入门学习笔记-Leture03-变换

隋义2022

于 2021-11-11 19:34:03 发布

阅读量315

点赞数

分类专栏：现代计算机图形学入门学习笔记文章标签：图形学

本文链接：https://blog.csdn.net/qq_33811591/article/details/121274601

版权

现代计算机图形学入门学习笔记专栏收录该内容

9 篇文章 1 订阅

订阅专栏

GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibili

变换分为缩放、旋转、平移

缩放

如下图从左边变换到右边

$x^{'}=s_{x}x$

$y^{'}=s_{y}y$

$\begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}=\begin{bmatrix} s_{x} & 0\\ 0 & s_{y} \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$

切变

如下图从左边变换到右边

$y^{'}=y$

$x^{'}=x+ya$

$\begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}=\begin{bmatrix} 1 & a\\ 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$

旋转

如下图从左边变换到右边，正方形边长为1

$(x,y)\approx >(x^{'}, y^{'})$

$\begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}=\begin{bmatrix} A & B\\ C & D\end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$

根据正方形右下顶点可得出

$\begin{bmatrix} \cos \theta \\\sin \theta \end{bmatrix}=\begin{bmatrix} A & B\\ C & D\end{bmatrix}\begin{bmatrix} 1\\ 0 \end{bmatrix}$

$\cos \theta =A$

$\sin \theta = C$

根据正方形左上顶点同理可得出

$\begin{bmatrix} -\sin \theta\\ \cos \theta \end{bmatrix}=\begin{bmatrix} A & B\\ C & D\end{bmatrix}\begin{bmatrix} 0\\ 1 \end{bmatrix}$

$-\sin \theta = B$

$\cos \theta = D$

所以旋转矩阵为：

$R_{\theta }=\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}$

$R_{-\theta }=\begin{bmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{bmatrix} = R_{\theta }^{T}$

根据定义可知：

$R_{-\theta } = R_{\theta }^{-1}$

所以旋转矩阵的逆矩阵等于其转置矩阵：

$R_{-\theta } = R_{\theta }^{-1} = R_{\theta }^{T}$

线性变换可以统一成一个矩阵变换

$x^{'}=ax+by$

$y^{'}=cx+dy$

$\begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}=\begin{bmatrix} A & B\\ C & D\end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$

$X^{'}=MX$

平移

如下图

$x^{'}=x+t_{x}$

$y^{'}=y+t_{y}$

$\begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}=\begin{bmatrix} x\\ y \end{bmatrix}+\begin{bmatrix} t_{x}\\ t_{y} \end{bmatrix}$

缩放、旋转、平移组合变换

Affine Map = Linear Map + Translation

仿射变换 = 线性变换 + 平移变换

$\begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}=\begin{bmatrix} a & b\\ c & d\end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}+\begin{bmatrix} t_{x}\\ t_{x} \end{bmatrix}$

目前无法使用一个矩阵变换，为了可以使用一个矩阵进行变换，引入齐次坐标。

齐次坐标

增加w坐标

2D $point = (x, y, 1)^{T}$

2D $vector = (x, y, 0)^{T}$

vector + vector = vector

point - point = vector

point + vector = point

point + point = middle point

$\begin{bmatrix} x_{1}\\ y_{1}\\ 1 \end{bmatrix}+\begin{bmatrix} x_{2}\\ y_{2}\\ 1 \end{bmatrix} = \begin{bmatrix} x_{1}+x_{2}\\ y_{1}+y_{2}\\ 2 \end{bmatrix} = \begin{bmatrix} x^{'}\\ y^{'}\\ w^{'} \end{bmatrix} = \begin{bmatrix} x^{'}/w^{'}\\ y^{'}/w^{'}\\ 1 \end{bmatrix} = \begin{bmatrix} ( x_{1}+x_{2})/2\\ ( y_{1}+y_{2})/2\\ 1 \end{bmatrix}$

齐次坐标下矩阵表示平移

$\begin{bmatrix} x^{'}\\ y^{'} \\ w^{'} \end{bmatrix}=\begin{bmatrix} 1 & 0& t_{x}\\ 0& 1& t_{y}\\ 0& 0& 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}=\begin{bmatrix} x+t_{x}\\ y+t_{y}\\ 1 \end{bmatrix}$

齐次坐标下仿射变换表示

$\begin{bmatrix} x^{'}\\ y^{'} \\ w^{'} \end{bmatrix}=\begin{bmatrix} a & b& t_{x}\\ c& d& t_{y}\\ 0& 0& 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}=\begin{bmatrix} ax+by+t_{x}\\ cx+dy+t_{y}\\ 1 \end{bmatrix}$

齐次坐标下缩放变换矩阵

$S(s_{x}, s_{y}) = \begin{bmatrix} s_{x}& 0& 0\\ 0& s_{y}& 0\\ 0& 0& 1 \end{bmatrix}$

齐次坐标下旋转变换矩阵

$R_{\alpha }=\begin{bmatrix} \cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha& 0\\ 0& 0& 1 \end{bmatrix}$

齐次坐标下平移变换矩阵

$T(t_{x}, t_{y}) = \begin{bmatrix} 1 & 0 & t_{x}\\ 0& 1& t_{y}\\ 0& 0& 1 \end{bmatrix}$

结合顺序

矩阵相乘不满足交换律，运算意义为自右向左结合。

$R_{\alpha }\cdot T_{(x, y)} \neq T_{(x, y)} \cdot R_{\alpha }$

点P先平移后旋转表示如下：

$P^{'} = R_{\alpha }\cdot T_{(x, y)}\cdot P$

点P先旋转后平移表示如下：

$P^{'} = T_{(x, y)}\cdot R_{\alpha }\cdot P$

分解复杂变换

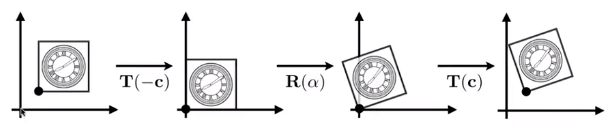
如下图要以图形左下顶点c为中心旋转，分解为3步：

1，平移图形至左下顶点c到原点，T(-c)。

2，旋转图形, R(a)。

3，平移图形至左下顶点回到原来位置, T(c)。

组合矩阵为：

$T_{(c)}\cdot R_{(\alpha )}\cdot T_{(-c)}$

3D变换

3D $point = (x, y, z, 1)^{T}$

3D $vector = (x, y, z, 0)^{T}$

(x, y, z, w)表示3D顶点(x/w, y/w, z/w)

3D仿射变换

$\begin{bmatrix} x^{'}\\ y^{'} \\ z^{'} \\ 1\end{bmatrix}=\begin{bmatrix} a & b& c&t_{x}\\ d& e& f&t_{y}\\ g& h& i&t_{z}\\0& 0& 0& 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\1 \end{bmatrix}$