动手学习深度学习笔记——PyTorch版（一）

torch基本操作

import torch

# 创建
x = torch.arange(12, dtype=torch.float32)	# 创建值为0-11的向量
y = torch.tensor([[1,2,3],[4,5,6]]) 		# 通过数组创建张量
torch.zeros((2,3,4))    					# 形状为 2*3*4 的全0张量
torch.ones((2,3,4))   						# 形状为 2*3*4 的全1张量
# 操作
x.shape  									# 查看张量形状
type(x)										# 查看x的数据类型
x.numel() 									# 查看张量元素个数
x = x.reshape(3, 4)      					# 改变张量形状 1*12 改为 3*4
torch.cat((x,y), dim=0)						# 按第0维连结张量
x.type(torch.float)							# 转换数据类型

# 计算：加减乘除，幂运算，指数运算 —— 均可按元素计算，可通过广播机制计算
# 广播机制：用于计算的张量形状如果对应某一个维度, 缺失的维度会自动复制填充
x+y, x-y,x*y,x/y,x**y, torch.exp(x)
# 生成逻辑张量 —— 必须对应一个或所有维度
x == torch.tensor([[0, 4, 5]])
x == torch.tensor([[1], [3]])
x == 2
x == torch.arange(12, dtype=torch.float32)
# 元素求和 —— 可按照多维, 结果形状相当于去除进行求和的维度
x.sum(axis=0)
x.sum(axis=[0, 1])
x.cumsum(axis=0)		# 累加求和
# 求均值
x.mean(axis=0)

# 内存
id(x)					# 类似c的指针
x = x+1 				# x的id会改变
x += 1					# x的id不变 —— 减少内存开销
x[:] = 1				# x的id不变
# 创建形状相同张量
z = torch.zeros_like(x)	# 创建一个大小与x相同的张量 

# torch转换为numpy数组
z = x.numpy()

# numpy数组转torch
torch.tensor(z)

# 大小为1的张量转python标量
a = torch.tensor([10])
a.item()

数据预处理

数据生成

import os

os.makedirs(os.path.join('.', 'data'), exist_ok=True)   # 创建文件夹 exist_ok=True表示文件存在时继续
data_file = os.path.join('.', 'data', 'test.csv')       # 创建文件
with open(data_file, 'w') as f:
    f.write('a,b,c\n')      # 列名
    f.write('NA,PC,362\n')  # 以下为各行数据
    f.write('4,NA,3110\n')
    f.write('5,NA,35\n')
    f.write('NA,NA,31\n')
    f.close()

数据预处理

import os
import pandas as pd

data_file = os.path.join('.', 'data', 'test.csv')
data = pd.read_csv(data_file)
print(data)

# 处理缺失数据 —— 常用删除和差值，以下通过平均值插值
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]	# 通过index location 分离首行和数据
inputs = inputs.fillna(inputs.mean())					# 通过平均值填充（非数值型不会填充）
# 将非数值单独分列（通过0-1表示），dummy_na=True 表示非数值列的NAN数据也单独分成一列
inputs = pd.get_dummies(inputs, dummy_na=True)	

# inputs.values 将 pandas 格式转为 numpy 数组格式，之后将其转为张量
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, y

线性代数

• 矩阵相乘代表一种空间扭曲

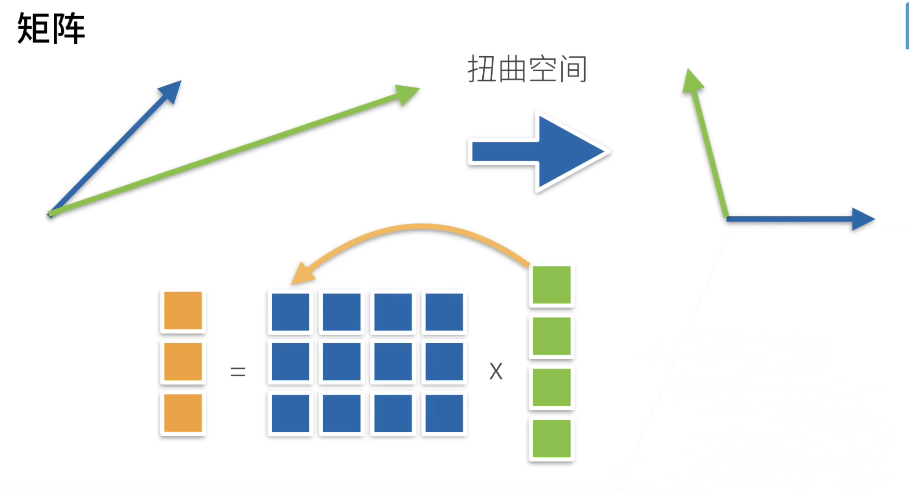
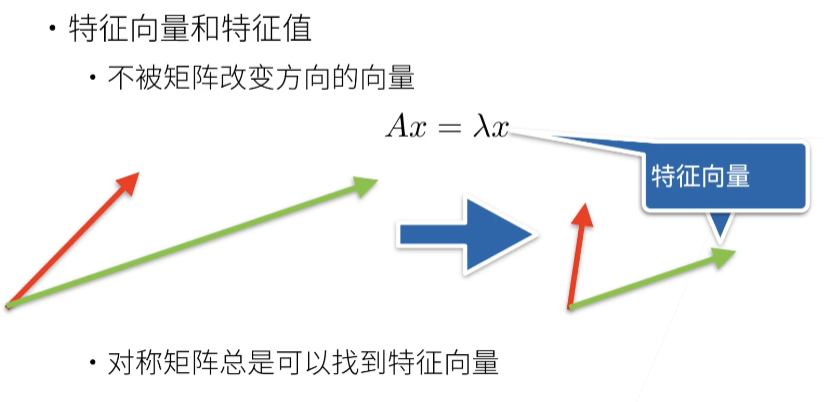
# 线性代数的实现
A = torch.arange(20).reshape(4,5)
B = torch.arange(15).reshape(5,3)
x = torch.arange(5)
A.T						# 矩阵的转置
A.clone()				# 得到A的副本，如果使用B=A，id(A)==id(B)
# 向量点积,
x.dot(x)								
torch.dot(x, x)
torch.sum(x*x)
# 矩阵与向量点积
torch.mv(A,x)
# 矩阵与矩阵点积
torch.mm(A,B)
# L1范数 —— 向量元素绝对值求和
torch.abs(u).sum()
# L2范数 —— 向量元素平方和的平方根
u = torch.tensor([3.0, 4.0])
torch.norm(u)
# 矩阵的 弗罗贝尼乌斯范数 —— 元素平方和的平方根
torch.norm(A.type(torch.float))

微积分

• 求导
  • 标量求导
  • 向量求导——梯度
  • 矩阵求导

标量对向量求导

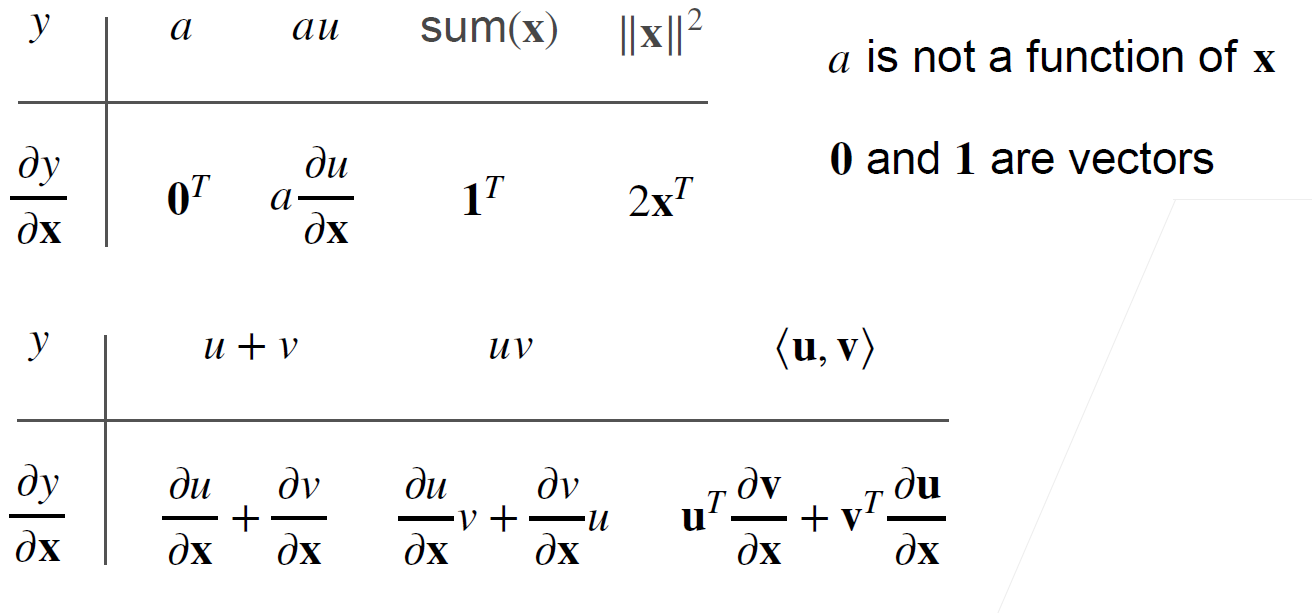
向量对向量求导

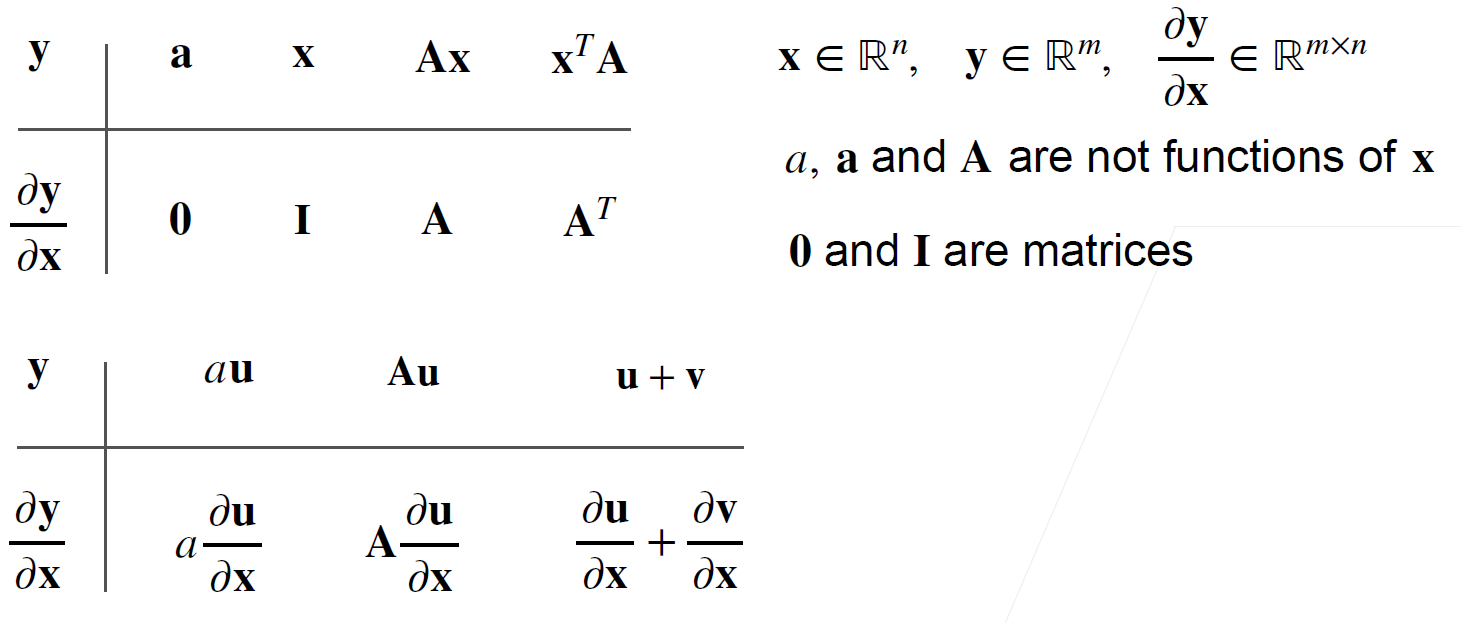
例一

例二

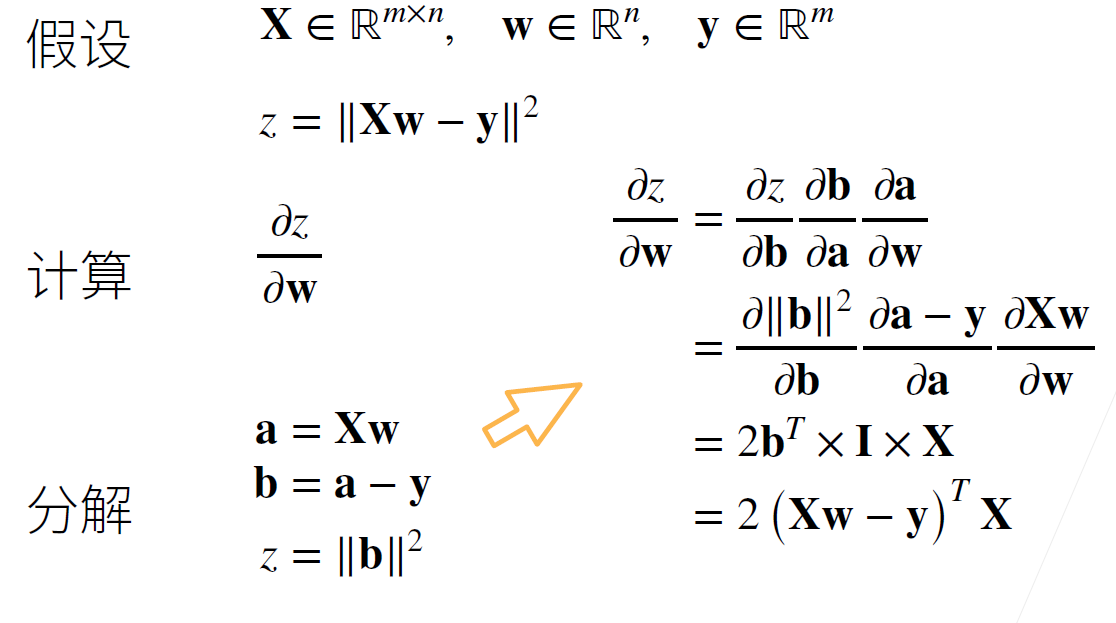
向量链式求导法则

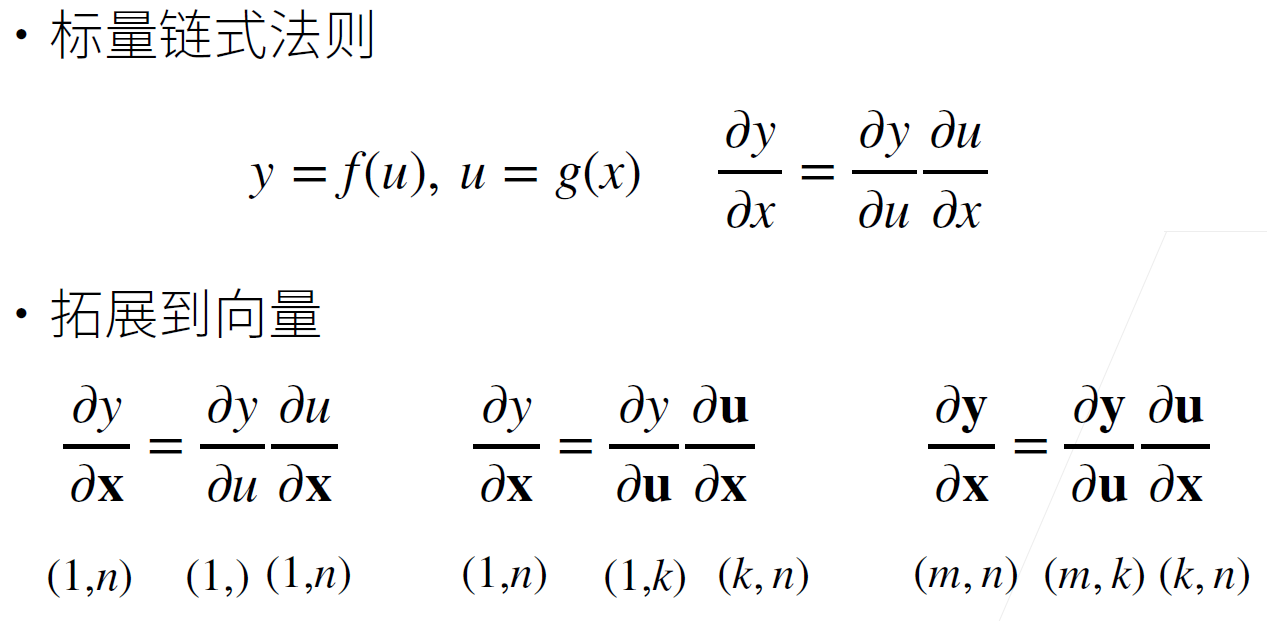
正向累积，反向累计（反向传递）

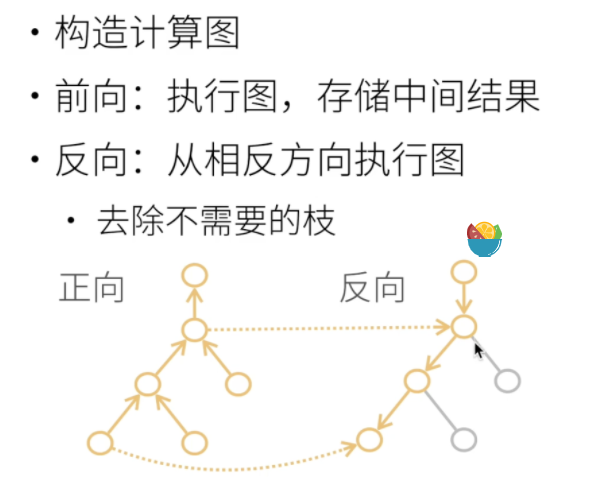
计算图

显式构造

• 有变量 a、b，公式 c = a + b；=> a=1，b=2 时，c=3

隐式构造

• 系统先记住 a=1，b=2；=> 有公式 c = a + b，则 c=3

正向累积：计算原函数结果和中间值

• 时间复杂度O(n)：操作子个数
• 空间复杂度O(1)

反向传递：计算梯度

• 时间复杂度O(n)：操作子个数
• 空间复杂度O(n)：需要先进行正向累积储存所有中间结果（耗资源）

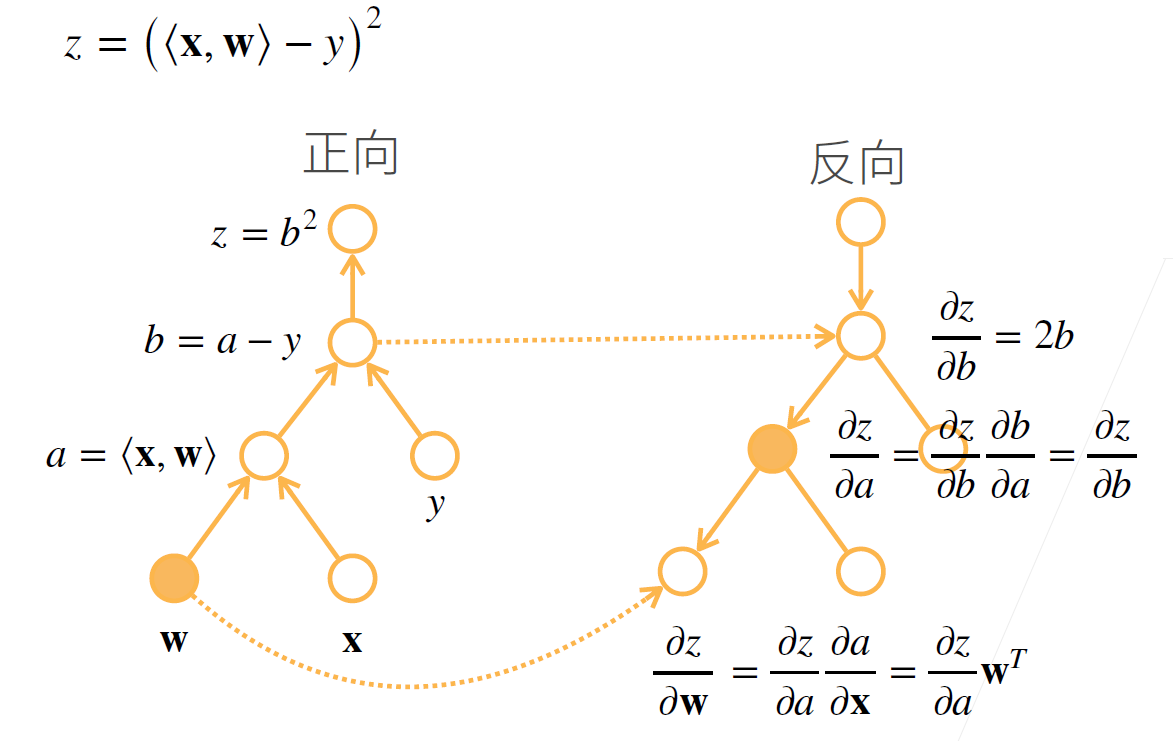
自动求导实现

标量求导

import torch

x = torch.arange(4.0, requires_grad=True)  # requires_grad 用于存储梯度
# x = torch.arange(4.0)
# x.requires_grad_(True) 	# 同等效果
x.grad == None  			# 初始默认为None
y = 2 * torch.dot(x, x)  	# 隐式构造计算图并执行 —— grad_fn
y.backward()				# 隐式调用反向传播函数自动计算y关于x每个分量的梯度
x.grad  					# 结果，默认累计梯度
x.grad.zero_()  			# 清零之前的值
y = x.sum() 			 	# 新函数
y.backward()
x.grad

• y.backward()

  • 若结果非标量

    • 通过 sum，例：y.sum().backward()
    • 显式调用 例：y.backward(torch.tensor([1, 1]))，1为梯度系数

    x = torch.tensor([1.,2],requires_grad=True)
    y = 2 * x
    y.backward(torch.tensor([1.0, 1]))
    print(x.grad)  # tensor([2., 2.])
    

  • $y=x1+x2=>\frac{dy}{dx}=\frac{dx1}{dx}+\frac{dx2}{dx}=>[\frac{dx1}{dx},\frac{dx2}{dx}]$

  • 默认执行后清空中间值，所以如果需要多次使用，需要加上retain_graph=True保存

    • y.backward(retain_graph=True)

向量对向量求导的自动求导示例——雅可比矩阵

$$\begin{gathered} y=[y_1,y_2,y_3]=[x_1^2+2x_2,x_2^2+4x_1,x_3^2+2x_1+x_2] \\ x=[x_1,x_2,x_3]=[1,2,3] \\ Jacobian=\left[\begin{array}{c}\frac{\partial y_1}{\partial x_1},\frac{\partial y_2}{\partial x_1},\frac{\partial y_3}{\partial x_1}\\ \frac{\partial y_1}{\partial x_2},\frac{\partial y_2}{\partial x_2},\frac{\partial y_3}{\partial x_2}\\ \frac{\partial y_1}{\partial x_3},\frac{\partial y_2}{\partial x_3},\frac{\partial y_3}{\partial x_3}\end{array}\right]=\left[\begin{array}{ccc}2x_1& 4& 2\\ 2& 2x_2& 1\\ 0& 0& 2x_3\end{array}\right]=\left[\begin{array}{ccc}2& 4& 2\\ 2& 4& 1\\ 0& 0& 6\end{array}\right] \end{gathered}$$

import torch

x = torch.tensor([[1.0, 2, 3]], requires_grad=True)
Jacobian = torch.zeros(3, 3)
y = torch.zeros(1, 3)
y[0, 0] = x[0, 0] ** 2 + 2 * x[0, 1]
y[0, 1] = x[0, 1] ** 2 + 4 * x[0, 0]
y[0, 2] = x[0, 2] ** 2 + 2 * x[0, 0] + x[0, 1]

y.backward(torch.tensor([[1, 0, 0]]), retain_graph=True)  # 第一列
Jacobian[:, 0] = x.grad
x.grad.zero_()

y.backward(torch.tensor([[0, 1, 0]]), retain_graph=True)  # 第二列
Jacobian[:, 1] = x.grad
x.grad.zero_()

y.backward(torch.tensor([[0, 0, 1]]), retain_graph=True)  # 第三列
Jacobian[:, 2] = x.grad
x.grad.zero_()

print(Jacobian)
# tensor([[2., 4., 2.],
#         [2., 4., 1.],
#         [0., 0., 6.]])

• 高阶求导需要分步计算，且每次计算前梯度需要清零

课程：动手学深度学习课程 (d2l.ai)