Concolic Testing for Deep Neural Networks
文章目录
DeepConcolic: Testing and Debugging Deep Neural Networks
简介
论文标题
- Concolic Testing for Deep Neural Networks
- 深度神经网络的符号测试
- 2018.9
贡献
- 我们开发了第一种DNNs的Concolic测试方法。
- 我们使用广泛的测试覆盖要求来评估该方法,包括Lipschitz连续性[1,3,20,29,30]和几个结构覆盖度量[15,18,23]。我们的实验表明,我们的新算法以一致的方式支持这种广泛的属性。
- 在软件工具DeepConcolic中实现了Concolic测试方法。实验结果表明,DeepConcolic具有较高的覆盖率,能够发现大量的对抗性实例。
工具地址: https://github.com/TrustAI/DeepConcolic
工具论文翻译: DeepConcolic: Testing and Debugging Deep Neural Networks
MC/DC论文翻译:Testing Deep Neural Networks
渣翻,尽力了...但这篇没怎么看懂
摘要
Concolic测试将程序执行和符号分析相结合,以探索软件程序的执行路径。本文提出了第一种深度神经网络(DNNs)的Concolic测试方法。更具体地说,我们将文献中研究的DNN的覆盖标准形式化,然后开发一种连贯的方法来执行Concolic测试,以增加测试覆盖。我们的实验结果表明,Concolic测试方法在获得高覆盖率和发现对抗性实例方面都是有效的。
介绍
深度神经网络(DNNs)在解决人工智能中的一系列难题方面发挥了重要作用,例如古老的围棋游戏、图像分类和自然语言处理。因此,许多潜在的应用被设想出来。然而,人们对这项技术是否适用于安全和安保关键系统提出了重大担忧,在这些系统中,错误的行为有危及人类生命或经济损失的风险。为了解决这些问题,需要对包含基于DNN的组件的(安全或安保)关键系统进行彻底验证。
软件行业依赖测试作为向涉众提供有关被测试软件产品或服务质量的信息的主要手段[12]。到目前为止,对DNN进行系统测试的尝试很少[15,18,23,25,30]。这些是基于具体执行的,例如,蒙特卡洛树搜索[30]或基于梯度的搜索[15,18,25],或者结合线性算术的解算器的符号执行[23]。与这些测试输入生成算法一起,提出了几个测试覆盖标准,包括神经元覆盖[18],一个受MC/DC[23]启发的标准,以及捕获特定神经元激活值以识别角落情况的标准[15]。这些方法都没有实现Concolic测试[8,22],它结合了具体的执行和符号分析来探索程序的执行路径,而这些路径是随机测试等技术很难覆盖的。
我们假设Concolic检测特别适用于DNNs。DNN的输入空间通常是高维的,这给随机测试带来了困难。例如,用于图像分类的DNN需要数万个像素作为输入。此外,由于隐含神经元的RELU激活函数的广泛使用,DNN中“执行路径”的数量太多而不能完全被符号执行所覆盖,Concolic测试可以通过具体地评估DNN的给定属性来将符号分析引导到特定的执行路径来降低这种复杂性。
在这篇文章中,我们提出了第一种DNNs的Concolic测试方法。该方法使用一组覆盖要求来参数化,我们使用有理数量化线性算术(QLAR)来表达这些要求。对于给定的覆盖率需求集合R,我们增量地生成一组测试输入,通过在具体执行和符号分析之间交替来提高覆盖率。在给定未满足的测试需求r的情况下,我们在当前测试套件中标识测试输入t,以便根据基于具体执行的评估,t接近满足r。之后,应用符号分析来获得满足r的新的测试输入t‘,然后将该测试输入t’添加到测试套中。这个过程反复进行,直到我们达到令人满意的覆盖率水平。
最后,将生成的测试套件传递给健壮性预言,其确定测试套件是否包括对抗性示例[24],即当相对于给定距离度量彼此接近时在其分类标签上不一致的测试用例对。健壮性的缺乏一直被认为是DNNs的一个主要弱点,敌意示例的发现和健壮性问题在机器学习、自动验证、网络安全和软件测试等领域都得到了积极的研究。
相关工作
我们简要回顾了现有的评估DNNs稳健性的努力和Concolic测试的最新进展
DNNs的鲁棒性
目前关于DNN健壮性的研究可以分为攻击性和防御性两类。攻击性方法侧重于启发式搜索算法(主要由DNN的前向梯度或代价梯度指导),以找到尽可能接近正确分类输入的对抗性示例。另一方面,防御工作的目标是增加DNNs的健壮性。进攻技术和防守技术之间存在着军备竞赛。
在本文中,我们将重点放在防御方法上。自动验证是一种很有前途的方法,其目的是为DNNs提供健壮性保证。主要的相关技术包括逐层穷举搜索[11]、使用约束求解器[14]的方法、全局优化方法[20]和抽象解释[7,16]来过度逼近DNN的行为。穷举搜索存在状态空间爆炸问题,蒙特卡罗树搜索可以缓解这一问题[30]。基于约束的方法仅限于具有数百个神经元的小型DNN。全局优化通过其处理大型DNN的能力改进了基于约束的方法,但其容量对需要扰动的输入维度的数量很敏感。过度近似分析的结果可能会因为错误警报而变得悲观。
将传统测试技术应用于DNN是困难的,并且尝试这样做的工作是较新的,例如[15,18,23,25,30]。受软件测试方法启发的方法通常使用覆盖标准来指导测试用例的生成;然后通过查询Oracle来搜索得到的测试套件中的对抗性示例。考虑的覆盖标准包括神经元覆盖[18],这类似于传统的语句覆盖。在[23]中使用了一组受MD/DC覆盖[10]启发的标准;Ma等人。[15]提出旨在捕捉神经元激活特定值的标准。田等人。[25]研究神经元覆盖率在Udacity-滴滴自动驾驶汽车挑战赛DNNs中检测敌意示例的效用。
我们现在讨论测试输入生成的算法。Wicker等人。[30]目的通过穷举变异测试来覆盖输入空间,这是有理论保证的,而在[15,18,25]中采用基于梯度的搜索算法来解决优化问题,Sun等人对此进行了研究。[23]应用线性规划。所有这些都不像我们在本文中所做的那样考虑Concolic测试和建模测试覆盖需求的一般方法。
Concolic测试
通过使用包括随机测试的特定输入来具体执行程序,可以低成本地测试大量输入。然而,在没有指导的情况下,生成的测试用例可能被限制在程序的执行路径的子集,并且探索包含错误的执行路径的概率可能非常低。在符号执行[5、26、32]中,对执行路径进行符号编码。现代约束求解器可以有效地确定编码的可行性,尽管性能仍然随着符号表示的大小的增加而降低。Concolic test[8,22]是一种自动生成测试输入的有效方法。它是一种混合软件测试技术,在具体执行(即对特定输入进行测试)和符号执行(将程序变量视为符号值的经典技术)之间交替[13]。
Concolic测试已经在软件测试中被常规应用,并且有广泛的工具可用,例如[4,8,22]。它从使用具体输入执行程序开始。在具体运行结束时,必须启发式地选择另一个执行路径。然后对这个新的执行路径进行符号化编码,并通过约束求解器求解得到的公式,以产生新的具体输入。具体执行和符号分析交替进行,直到达到所需的结构覆盖率。
影响Concolic测试性能的关键因素是用来选择下一条执行路径的启发式算法。虽然有一些简单的方法,如随机搜索和深度优先搜索,但更仔细设计的启发式算法可以实现更好的覆盖[4,9]。自动生成用于Concolic测试的搜索启发式是一个活跃的研究领域[6,27]。
与相关工作对比
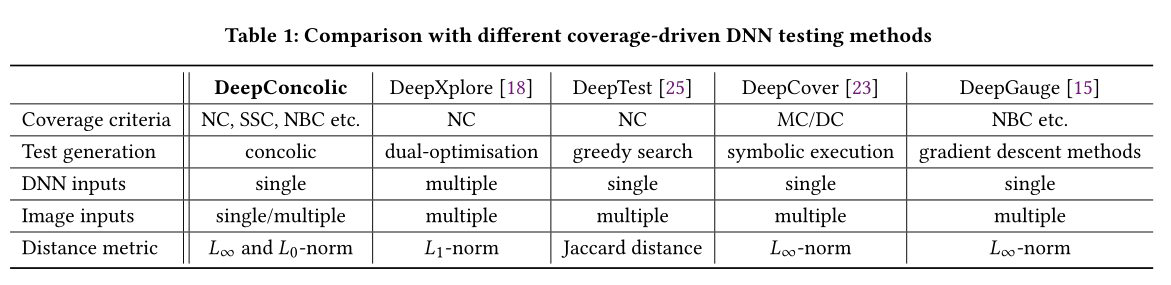
我们简要总结了我们的Concolic测试方法DeepConcolic与其他现有的覆盖驱动的DNN测试方法DeepXplore[18]、DeepTest[25]、DeepCover[23]和DeepGauge[15]之间的异同。详细信息如表1所示,其中NC、SSC和NBC分别是神经元覆盖、SS覆盖和神经元边界覆盖的缩写。除了DeepConcolic的Concolic本质外,我们还观察到以下不同之处。
- DeepConcolic是通用的,能够将覆盖需求作为输入;其他方法是特别的,并且根据特定的需求进行定制。
- DeepXplore需要一组DNN来探索多个渐变方向。其他方法,包括DeepConcolic,只需要一个DNN。
- 与其他方法相比,DeepConcolic可以通过从单个输入开始实现良好的覆盖;其他方法需要一组非常重要的输入。
- 到目前为止,最佳距离度量还没有结论。DeepConcolic可以用期望的范数距离度量||·||参数化。
此外,DeepConcolic的特点是在测试输入生成和测试预言之间进行了清晰的分离。这非常适合传统测试用例生成。其他方法使用Oracle作为其目标的一部分,以指导测试输入的生成。
深度神经网络
(前馈和深度)神经网络,或称DNN,是一个元组
N
=
\mathcal{N}=
N=
(
L
,
T
,
Φ
)
(L, T, \Phi)
(L,T,Φ) ,使得
L
=
{
L
k
∣
k
∈
{
1
,
…
,
K
}
}
L=\left\{L_{k} | k \in\{1, \ldots, K\}\right\}
L={Lk∣k∈{1,…,K}} 是层的集合,
T
⊆
T \subseteq
T⊆
L
×
L
L \times L
L×L 是层之间的连接集合,
Φ
=
{
ϕ
k
∣
k
∈
\Phi=\left\{\phi_{k} | k \in\right.
Φ={ϕk∣k∈
{
2
,
…
,
K
}
}
\{2, \ldots, K\}\}
{2,…,K}} 是一组激活函数。每层
L
k
L_{k}
Lk 由
s
k
s_{k}
sk 个神经元组成,第l层神经元记为
n
k
,
l
n_{k, l}
nk,l。我们用
v
k
,
l
v_{k, l}
vk,l 表示$n_{k, l} $的值。隐层的神经元的值需要通过一个校正线性单元(RELU)[17]。为方便起见,我们使用
u
k
,
l
u_{k, l}
uk,l 表示在RELU激活之前的值
v
k
,
l
=
ReLU
(
u
k
,
l
)
=
{
u
k
,
l
if
u
k
,
l
≥
0
0
otherwise
v_{k, l}=\operatorname{ReLU}\left(u_{k, l}\right)=\left\{\begin{array}{ll} u_{k, l} & \text { if } u_{k, l} \geq 0 \\ 0 & \text { otherwise } \end{array}\right.
vk,l=ReLU(uk,l)={uk,l0 if uk,l≥0 otherwise
除了输入之外,每个神经元通过预定义的权重连接到前一层中的神经元,使得
∀
1
<
k
≤
K
\forall 1<k \leq K
∀1<k≤K,
∀
1
≤
l
≤
s
k
\forall 1 \leq l \leq s_{k}
∀1≤l≤sk
u
k
,
l
=
∑
1
≤
h
≤
s
k
−
1
{
w
k
−
1
,
h
,
l
⋅
v
k
−
1
,
h
}
+
b
k
,
l
u_{k, l}=\sum_{1 \leq h \leq s_{k-1}}\left\{w_{k-1, h, l} \cdot v_{k-1, h}\right\}+b_{k, l}
uk,l=1≤h≤sk−1∑{wk−1,h,l⋅vk−1,h}+bk,l
其中
w
k
−
1
,
h
,
l
w_{k-1, h, l}
wk−1,h,l是用于
n
k
−
1
,
h
n_{k-1, h}
nk−1,h(即,第k层−1的第h个神经元)和
n
k
,
l
n_{k, l}
nk,l即,第k层的第l个神经元)之间的连接的预训练权重,
b
k
,
l
b_{k, l}
bk,l是偏置。
最后,对于任何输入,神经网络分配一个标签,即,具有最大值的输出层的神经元的索引,即, label = argmax 1 ≤ l ≤ s K { v K , l } \text { label }=\operatorname{argmax}_{1 \leq l \leq s_{K}}\left\{v_{K, l}\right\} label =argmax1≤l≤sK{vK,l}
-
由于RELU的存在,神经网络是一个高度非线性的函数。在本文中,我们使用变量x对输入域 D L 1 D_{L_{1}} DL1中所有可能的输入进行取值,并使用t,t1,t2,.。表示具体的输入。给定特定的输入t,我们说DNN N \mathcal{N} N 是实例化的,并且我们使用 N [ t ] \mathcal{N}[t] N[t] 来表示该网络实例。
-
当给出输入时,确定DNN中每个RELU操作符的激活或非激活。
我们注意到,虽然为了简单起见,该定义集中在具有全连通和卷积层的DNN上,如实验(第10节)所示,我们的方法也适用于其他流行的层,例如,在最新的DNN中使用的MaxPooling。
DNNS的覆盖测试
激活模式
软件程序有一组具体的执行路径。类似地,DNN有一组称为激活模式的线性行为[23]。
定义4.1(激活模式)。给定网络
N
\mathcal{N}
N 和输入t,
N
[
t
]
\mathcal{N}[t]
N[t] 的激活模式是将隐藏神经元集合映射到{true,false}的函数
a
p
[
N
,
t
]
a p[\mathcal{N}, t]
ap[N,t] 。如果N是上下文中清晰明了的,我们将
a
p
[
N
,
t
]
a p[\mathcal{N}, t]
ap[N,t]写为
a
p
[
t
]
a p[t]
ap[t] 。对于激活模式
a
p
[
t
]
a p[t]
ap[t] ,我们用
a
p
[
t
]
k
,
i
a p[t]_{k, i}
ap[t]k,i 表示神经元
n
k
,
i
n_{k, i}
nk,i 的RELU算子是否被激活。正式地说,
a
p
[
t
]
k
,
l
=
false
≡
u
[
t
]
k
,
l
<
v
[
t
]
k
,
l
a
p
[
t
]
k
,
l
=
true
≡
u
[
t
]
k
,
l
=
v
[
t
]
k
,
l
\begin{array}{l} a p[t]_{k, l}=\text { false } \quad \equiv \quad u[t]_{k, l}<v[t]_{k, l} \\ a p[t]_{k, l}=\text { true } \quad \equiv \quad u[t]_{k, l}=v[t]_{k, l} \end{array}
ap[t]k,l= false ≡u[t]k,l<v[t]k,lap[t]k,l= true ≡u[t]k,l=v[t]k,l
直观地,如果神经元
n
k
,
l
n_{k, l}
nk,l的REU被激活,则
a
p
[
t
]
k
,
l
=
a p[t]_{k, l}=
ap[t]k,l= true,否则
a
p
[
t
]
k
,
l
=
a p[t]_{k, l}=
ap[t]k,l= false。
给定DNN实例 N [ t ] \mathcal{N}[t] N[t],每个RELU操作符的行为是固定的,并且这导致特定的激活模式映射 a p [ t ] , a p[t], ap[t],,其可以通过使用线性规划(LP)模型[23]来编码。
由于在实际相关的DNN中有大量的神经元,所以计算覆盖DNN的所有激活模式的测试套件是困难的。因此,我们根据特定的覆盖标准识别激活模式的子集,然后生成覆盖这些激活模式的测试输入。
形式化测试覆盖标准
我们使用有理数量化线性算术(QLAR)的特定片段来表示给定DNN的测试集上的覆盖要求。这使我们能够为各种覆盖标准提供单一的测试输入生成算法(第8节)。我们将片段中的公式集表示为DR。
定义4.2。给定一个网络
N
\mathcal{N}
N,我们将
I
V
=
{
x
,
x
1
,
x
2
,
…
}
I V=\left\{x, x_{1}, x_{2}, \ldots\right\}
IV={x,x1,x2,…} 写为一组范围在网络的所有输入
D
L
1
D_{L_{1}}
DL1 上的变量。我们定义
V
=
{
u
[
x
]
k
,
l
,
v
[
x
]
k
,
l
∣
1
≤
k
≤
K
,
1
≤
l
≤
s
k
,
x
∈
I
V
}
V=\left\{u[x]_{k, l}, v[x]_{k, l} | 1 \leq k \leq K, 1 \leq l \leq\right. \left.s_{k}, x \in I V\right\}
V={u[x]k,l,v[x]k,l∣1≤k≤K,1≤l≤sk,x∈IV} 为一组取值于有理数上的变量。我们修复了DR公式的以下语法:
r
:
:
=
Q
x
.
e
∣
Q
x
1
,
x
2
.
e
e
:
:
=
a
⋈
0
∣
e
∧
e
∣
¬
e
∣
∣
{
e
1
,
…
,
e
m
}
∣
⋈
q
a
:
:
=
w
∣
c
⋅
w
∣
p
∣
a
+
a
∣
a
−
a
\begin{array}{l} r::=Q x . e | Q x_{1}, x_{2} . e \\ e::=a \bowtie 0|e \wedge e| \neg e||\left\{e_{1}, \ldots, e_{m}\right\} | \bowtie q \\ a::=w|c \cdot w| p|a+a| a-a \end{array}
r::=Qx.e∣Qx1,x2.ee::=a⋈0∣e∧e∣¬e∣∣{e1,…,em}∣⋈qa::=w∣c⋅w∣p∣a+a∣a−a
其中
Q
∈
{
∃
,
∀
}
,
w
∈
V
,
c
,
p
∈
R
,
q
∈
N
,
⋈
∈
{
≤
,
<
,
=
,
>
,
≥
}
Q \in\{\exists, \forall\}, w \in V, c, p \in \mathbb{R}, q \in \mathbb{N}, \bowtie \in\{\leq,<,=,>, \geq\}
Q∈{∃,∀},w∈V,c,p∈R,q∈N,⋈∈{≤,<,=,>,≥} 并且
x
,
x
1
,
x
2
∈
I
V
.
x, x_{1}, x_{2} \in I V .
x,x1,x2∈IV. 我们称r为覆盖要求,e为布尔公式,a为算术公式。如果不允许使用否定运算符,我们称逻辑为DR+。我们用R表示一组覆盖要求公式。
公式∃x.e表示存在输入x使得e为真,而∀x.e表示对于所有输入x ,e为真。公式∃x1、x2.e和∀x1、x2.e具有类似的含义,除了它们在两个输入x1和x2上量化。如果集合{e1,.,em}中的真布尔表达式的数量与q相关,则布尔表达式 ∣ { e 1 , … , e m } ∣ ⋈ q \left|\left\{e_{1}, \ldots, e_{m}\right\}\right| \bowtie q ∣{e1,…,em}∣⋈q 为TRUE。布尔公式和算术公式中的其他运算符都有其标准含义。
尽管V不包括指定激活模式ap[x]的变量,但我们可以编写
a
p
[
x
1
]
k
,
l
=
a
p
[
x
2
]
k
,
l
and
a
p
[
x
1
]
k
,
l
≠
a
p
[
x
2
]
k
,
l
a p\left[x_{1}\right]_{k, l}=a p\left[x_{2}\right]_{k, l} \text { and } a p\left[x_{1}\right]_{k, l} \neq a p\left[x_{2}\right]_{k, l}
ap[x1]k,l=ap[x2]k,l and ap[x1]k,l=ap[x2]k,l
要求x1和x2在神经元
n
k
,
l
n_{k, l}
nk,l上分别具有相同和不同的激活行为。这些条件可以使用公式(3)中的表达式以上述语法表示。此外,两个输入之间的一些基于范数的距离可以使用我们的语法来表示。例如,我们可以使用约束集
{
x
1
(
i
)
−
x
2
(
i
)
≤
q
,
x
2
(
i
)
−
x
1
(
i
)
≤
q
∣
i
∈
{
1
,
…
,
s
1
}
}
\left\{x_{1}(i)-x_{2}(i) \leq q, x_{2}(i)-x_{1}(i) \leq q | i \in\left\{1, \ldots, s_{1}\right\}\right\}
{x1(i)−x2(i)≤q,x2(i)−x1(i)≤q∣i∈{1,…,s1}}
表示||x1−x2||∞≤q,即,我们可以约束两个输入x1和x2之间的切比雪夫距离L∞,其中x(I)是输入向量x的第i维。
语义学。我们通过测试集T定义覆盖需求r的可满足性
定义4.3。给定测试输入集合T和覆盖要求r,可满足性关系T|=r定义如下。
- T ∣ = ∃ x . e \mathcal{T}|=\exists x . e T∣=∃x.e 如果存在某种测试 t ∈ T t \in \mathcal{T} t∈T 使得 T = \mathcal{T}= T= e [ x ↦ t ] , e[x \mapsto t], e[x↦t], 其中 e [ x ↦ t ] e[x \mapsto t] e[x↦t] 表示用t代替x的出现的表达式e
- T = ∃ x 1 , x 2 . e \mathcal{T}=\exists x_{1}, x_{2} . e T=∃x1,x2.e 如果存在两个测试 t 1 , t 2 ∈ T t_{1}, t_{2} \in \mathcal{T} t1,t2∈T 使得 T = e [ x 1 ↦ t 1 ] [ x 2 ↦ t 2 ] \mathcal{T}=e\left[x_{1} \mapsto t_{1}\right]\left[x_{2} \mapsto t_{2}\right] T=e[x1↦t1][x2↦t2]
∀公式的情况类似。对于对输入t的布尔表达式e的求值,我们有
T = a ⋈ 0 if a ⋈ 0 T ∣ = e 1 ∧ e 2 if T ∣ = e 1 and T ∣ = e 2 T ∣ = ¬ e if not T ∣ = e T ∣ = ∣ { e 1 , … , e m } ∣ ⋈ q if ∣ { e i ∣ T = e i , i ∈ { 1 , … , m } } ∣ ⋈ q \begin{array}{l} \mathcal{T}=a \bowtie 0 \text { if } a \bowtie 0 \\ \mathcal{T} |=e_{1} \wedge e_{2} \text { if } \mathcal{T} |=e_{1} \text { and } \mathcal{T} |=e_{2} \\ \mathcal{T} |=\neg e \text { if not } \mathcal{T} |=e \\ \mathcal{T}|=|\left\{e_{1}, \ldots, e_{m}\right\} | \bowtie q \text { if }\left|\left\{e_{i} | \mathcal{T}=e_{i}, i \in\{1, \ldots, m\}\right\}\right| \bowtie q \end{array} T=a⋈0 if a⋈0T∣=e1∧e2 if T∣=e1 and T∣=e2T∣=¬e if not T∣=eT∣=∣{e1,…,em}∣⋈q if ∣{ei∣T=ei,i∈{1,…,m}}∣⋈q
对于对输入t的算术表达式a的求值
- u [ t ] k , l u[t]_{k, l} u[t]k,l 和 v [ t ] k , l v[t]_{k, l} v[t]k,l 测试t的DNN的激活模式中导出它们的值,并且 c ⋅ u [ t ] k , l c \cdot u[t]_{k, l} c⋅u[t]k,l 和 c ⋅ v [ t ] k , l c \cdot v[t]_{k, l} c⋅v[t]k,l 具有标准含义,其中c是系数,
- p、a1+a2和a1−a2具有标准语义。
请注意,T是有限的。将满足关系的定义推广到输入子空间是微不足道的。
复杂性。在给定网络N、DR需求公式和测试集T的情况下,可以在大小为T的多项式的时间内完成检查T|=r。确定是否存在具有T|=r的测试集T是NP-complete的。
测试覆盖率指标
现在,我们可以通过提供测试套件的一组需求来定义测试覆盖标准。覆盖率度量以标准方式定义为测试套件T中的测试用例满足的测试需求的百分比
定义4.4(Coverage Metric))。给定网络N、表示为DR公式的测试覆盖要求集合R和测试套件T,测试覆盖度量M(R,T)如下:
M
(
R
,
T
)
=
∣
{
r
∈
R
∣
T
∣
=
r
}
∣
∣
R
∣
M(\mathfrak{R}, \mathcal{T})=\frac{|\{r \in \mathfrak{R}|\mathcal{T}|=r\}|}{|\mathfrak{R}|}
M(R,T)=∣R∣∣{r∈R∣T∣=r}∣
覆盖率用作测试中的DNN的安全性置信度的代理度量。
具体覆盖要求
在这一部分中,我们给出了DNNs的几个重要覆盖准则的DR+公式,包括文献中的Lipschitz连续性[1,3,20,29,30]和测试覆盖准则[15,18,23]。我们考虑的标准在句法上与传统软件测试中的结构测试覆盖标准有相似之处。Lipschitz连续性是语义的,特定于DNNs,并且已经被证明与卷积DNNs的理论理解[29]以及DNNs[20,30]和生成性对抗性网络[1]的健壮性密切相关。这些标准已经在文献中使用各种形式主义和方法进行了研究。
每个测试覆盖标准都会产生一组测试覆盖要求。下面,我们将分别讨论[15,18,23]中的三个覆盖标准。我们使用||t1(−)t2||q来表示两个输入t1和t2相对于给定距离度量||·||q之间的距离。度量||·||q可以是例如基于范数的度量,例如L0范数(汉明距离)、L2范数(欧几里得距离)或L切比雪夫范数(∞距离),或者结构相似距离,例如SSIM[28]。在下面,我们固定一个距离度量,并简单地写为||t1−t2||。第10节详细介绍了我们在实验中使用的特定度量标准。
我们可以考虑对一组输入子空间的要求。给定实数b,我们可以生成DL1的子空间的有限集合S(DL1,b),使得对于所有的输入x1,x2∈DL1,如果||x1−x2||≤b,则存在一个子空间X∈S(DL1,b)使得x1,x2∈X。子空间可以重叠。通常,每个子空间X∈S(dl1,b)可以用盒约束来表示,例如,X=[l,u]s1,因此t∈X可以用如下的布尔表达式来表示。
⋀
i
=
1
s
1
x
(
i
)
−
u
≤
0
∧
x
(
i
)
−
l
≥
0
\bigwedge_{i=1}^{s_{1}} x(i)-u \leq 0 \wedge x(i)-l \geq 0
i=1⋀s1x(i)−u≤0∧x(i)−l≥0
Lipschitz连续性
在[20,24]中,Lipschitz连续性已被证明适用于一大类DNN,包括用于图像分类的DNN
定义5.1(Lipschitz连续性)。如果存在实常数c≥0,使得对于所有x1,x2∈dl1,网络N称为李普希茨连续的:
∥
v
[
x
1
]
1
−
v
[
x
2
]
1
∥
≤
c
⋅
∥
x
1
−
x
2
∥
\left\|v\left[x_{1}\right]_{1}-v\left[x_{2}\right]_{1}\right\| \leq c \cdot\left\|x_{1}-x_{2}\right\|
∥v[x1]1−v[x2]1∥≤c⋅∥x1−x2∥
回想一下,v[x]1表示输入层中神经元激活值的向量。值c称为Lipschitz常数,这样的最小常数称为最佳Lipschitz常数,记为
c
b
e
s
t
c_{b e s t}
cbest。
由于 c b e s t c_{b e s t} cbest的计算是NP-hard问题,较小的c可以显著提高验证算法的性能[20,30,31],因此确定给定的c是否对于整个输入空间DL1或某些子空间是Lipschitz常数是有趣的。可以使用以下要求指导Lipschitz连续性测试。
定义5.2(Lipschitz Coverage)。给定实数c>0和整数b>0,Lipschitz覆盖的要求集合
ℜ
L
i
p
(
b
,
c
)
\Re_{L i p}(b, c)
ℜLip(b,c)为
{
∃
x
1
,
x
2
⋅
(
∥
v
[
x
1
]
1
−
v
[
x
2
]
1
∥
−
c
⋅
∥
x
1
−
x
2
∥
>
0
)
∧
x
1
,
x
2
∈
X
∣
X
∈
S
(
D
L
1
,
b
)
}
\begin{array}{l} \left\{\exists x_{1}, x_{2} \cdot\left(\left\|v\left[x_{1}\right]_{1}-v\left[x_{2}\right]_{1}\right\|-c \cdot\left\|x_{1}-x_{2}\right\|>0\right)\right. \\ \left.\quad \wedge x_{1}, x_{2} \in X | X \in \mathcal{S}\left(D_{L_{1}}, b\right)\right\} \end{array}
{∃x1,x2⋅(∥v[x1]1−v[x2]1∥−c⋅∥x1−x2∥>0)∧x1,x2∈X∣X∈S(DL1,b)}
其中
S
(
D
L
1
,
b
)
\mathcal{S}\left(D_{L_{1}}, b\right)
S(DL1,b)被赋予输入子空间。
直观地,对于每个X∈S(DL1,b),该要求表示存在两个输入x1和x2,它们驳斥了c是N的Lipschitz常数。通常不可能获得完全的Lipschitz覆盖,因为可能存在不一致的 r ∈ ℜ L i p ( b , c ) r \in \Re_{L i p}(b, c) r∈ℜLip(b,c)。因此,测试用例生成算法的目标是生成尽可能满足标准的测试用例集T。
神经元覆盖率
神经元覆盖率(NC)[18]是传统软件测试中语句覆盖率在DNNs上的改编。它的定义如下。
定义5.3。DNN的神经元覆盖需要测试套件T,使得对于任何隐藏的神经元k,i,存在测试用例t∈T,使得AP[t]k,i=TRUE
这是用以下要求 ℜ N C \Re_{N C} ℜNC来形式化的,每个要求 ℜ N C \Re_{N C} ℜNC都表示存在具有激活神经元nk,i,即AP[x]k,i=真的输入x的测试。
定义5.4(NC Requirements).。设置神经元覆盖的
ℜ
N
C
\Re_{N C}
ℜNC覆盖要求为
{
∃
x
.
a
p
[
x
]
k
,
i
=
true
∣
2
≤
k
≤
K
−
1
,
1
≤
i
≤
s
k
}
\left\{\exists x . a p[x]_{k, i}=\text { true } | 2 \leq k \leq K-1,1 \leq i \leq s_{k}\right\}
{∃x.ap[x]k,i= true ∣2≤k≤K−1,1≤i≤sk}
修改条件/决策(MC/DC)覆盖范围
在[23]中,受传统软件测试中MC/DC覆盖的启发,提出了一个由四个测试标准组成的家族。我们将在这里仅讨论Sign-Sign Coverage(SSC)。根据[23],可以将每个神经元nk+1,j视为其中前一层(即,第k层)中的神经元是定义其激活值的条件的判定,如公式(2)中所示。使MC/DC适应DNNs,我们必须证明所有条件神经元都能独立地决定决策神经元的结果。在SSC覆盖的情况下,我们说,如果一个判决或条件神经元的激活函数的符号改变,那么它的值就会改变。因此,SSC覆盖的要求由以下集合定义。
定义 5.5 (SSC Requirements). 对于 SCC 覆盖,我们对于一对儿神经元 α = ( n k , i , n k + 1 , j ) \alpha=\left(n_{k, i}, n_{k+1, j}\right) α=(nk,i,nk+1,j)定义覆盖要求 R e S S C ( α ) Re_{S S C}(\alpha) ReSSC(α)
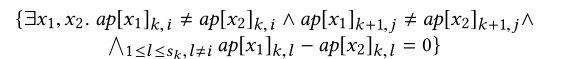
我们就会得到
ℜ
S
S
C
=
⋃
2
≤
k
≤
K
−
2
,
1
≤
i
≤
s
k
,
1
≤
j
≤
s
k
+
1
ℜ
S
S
C
(
(
n
k
,
i
,
n
k
+
1
,
j
)
)
\Re_{S S C}=\bigcup_{2 \leq k \leq K-2,1 \leq i \leq s_{k}, 1 \leq j \leq s_{k+1}} \Re_{S S C}\left(\left(n_{k, i}, n_{k+1, j}\right)\right)
ℜSSC=2≤k≤K−2,1≤i≤sk,1≤j≤sk+1⋃ℜSSC((nk,i,nk+1,j))
也就是说,对于相邻的两层k和k+1中的每对神经元(nk,i,nk+1,j),我们需要两个输入x1和x2,使得nk,i的符号变化独立地影响nk+1,j的符号变化。要求k层的其他神经元保持它们的符号在x1和x2之间,以确保该变化是独立的。SS覆盖的想法(以及[23]中的所有其他标准)是为了确保不仅需要测试特征的存在,而且必须测试较不复杂的特征对较复杂的特征的影响。
神经元边界覆盖
神经元边界覆盖(NBC)[15]旨在覆盖超过给定界限的神经元激活值。它可以用以下公式表示。
Definition 5.6 (Neuron Boundary Coverage Requirements). 给与两个边界
h
=
{
h
k
,
i
∣
2
≤
k
≤
K
−
1
,
1
≤
i
≤
s
k
}
h=\left\{h_{k, i} | 2 \leq k \leq K-1,1 \leq i \leq s_{k}\right\}
h={hk,i∣2≤k≤K−1,1≤i≤sk} 和
l
=
l=
l=
{
l
k
,
i
∣
2
≤
k
≤
K
−
1
,
1
≤
i
≤
s
k
}
,
\left\{l_{k, i} | 2 \leq k \leq K-1,1 \leq i \leq s_{k}\right\},
{lk,i∣2≤k≤K−1,1≤i≤sk}, 覆盖要求
ℜ
N
B
C
(
h
,
l
)
\Re_{N B C}(h, l)
ℜNBC(h,l) 为
{
∃
x
.
u
[
x
]
k
,
i
−
h
k
,
i
>
0
,
∃
x
.
u
[
x
]
k
,
i
−
l
k
,
i
<
0
∣
2
≤
k
≤
K
−
1
,
1
≤
i
≤
s
k
}
\begin{array}{c} \left\{\exists x . u[x]_{k, i}-h_{k, i}>0, \exists x . u[x]_{k, i}-l_{k, i}<0 |\right. \\ \left.2 \leq k \leq K-1,1 \leq i \leq s_{k}\right\} \end{array}
{∃x.u[x]k,i−hk,i>0,∃x.u[x]k,i−lk,i<0∣2≤k≤K−1,1≤i≤sk}
其中,hk,i和lk,i是神经元激活值nk的上界和下界。
我们的方法概述
本节概述了我们为给定DNN生成测试套件的方法。我们的方法在DNN激活模式的具体评估和新输入的符号生成之间交替。我们方法的伪代码如算法1所示,如图1所示。
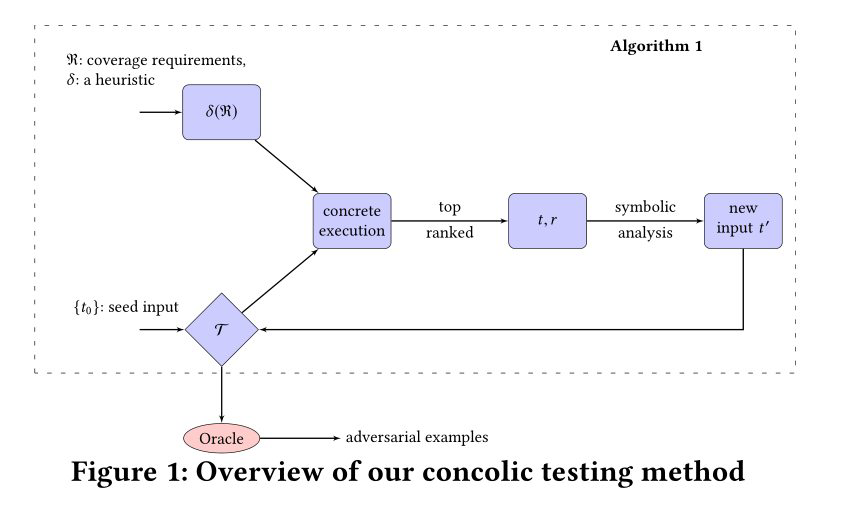
算法1将DNN N \mathcal{N} N、DNN的输入 t 0 t_{0} t0 、启发式 δ \delta δ,和覆盖要求的集合 ℜ \Re ℜ 作为输入,并产生测试集 T \mathcal{T} T 作为输出。测试套件 T \mathcal{T} T 最初仅包含给定的测试输入$t_{0} $。一旦需求 r ∈ R r \in \mathfrak{R} r∈R 被 T \mathcal{T} T满足,即 T ∣ = r \mathcal{T} |=r T∣=r,该算法就从 ℜ \Re ℜ 中移除它。

函数REQUIRED_EVALUATION(第7行)(其详细信息在第7节中给出)查找一对(t,r)的输入和需求,根据我们的具体评估,这对输入和需求是最有希望的符合要求的新测试用例的候选者。启发式δ是将带有运算符∃的公式r映射到优化问题的转换函数。这一步有赖于具体的执行。
在获得(t,r)之后,应用Symbol_Analysis(第8行)(其详细信息在第8节中)来获得新的具体输入t‘。然后应用函数VALIDATION_CHECK(第9行),其详细信息在第9节中给出,以检查新输入是否有效。如果是,则将该测试添加到测试套件中。否则,重复排序和符号输入生成,直到超过给定的计算成本,之后认为需求的测试生成失败。这记录在集合F中。
当已经满足所有测试要求(即,R=∅)或不能满足R中的其他要求(即,F=R)时,该算法终止。然后,该算法返回当前测试套件T。
最后,如图1所示,算法1生成的测试套件T被传递给Oracle,以评估DNN的健壮性。oracle的详细内容在第9节。
排名覆盖要求
本节介绍我们针对算法1第7行的方法。给定一组尚未满足的要求R、启发式δ和当前的测试输入集合T,目标是选择具体输入t∈T和要求r∈R,这两个都将在稍后的符号方法中用于计算下一个具体输入t‘(将在第8节中给出)。t和r的选择是通过一系列具体执行来完成的。
总体思路如下。对于所有需求
r
∈
ℜ
r \in \Re
r∈ℜ ,我们通过将运算符 argopt opt∈
{
max
,
min
}
\{\max , \min \}
{max,min} 用于将通过在
T
\mathcal{T}
T中具体执行测试来将r转换为
δ
(
r
)
\delta(r)
δ(r) 。由于R可能包含多个需求,我们返回(t,r)对,使得
r
=
arg
max
r
{
v
a
l
(
t
,
δ
(
r
)
)
∣
r
∈
ℜ
}
r=\arg \max _{r}\{v a l(t, \delta(r)) | r \in \Re\}
r=argrmax{val(t,δ(r))∣r∈ℜ}
请注意,在评估argopt公式(例如,argminx a:e)时,如果返回输入t∈T,我们可能还需要该值(minx a:e)。我们使用val(t,δ®)来表示返回的输入t和需求公式r的这样一个值。
公式 δ ( r ) \delta(r) δ(r) 与一组约束一起是优化目标。稍后我们将在7.1节中给出几个示例。在下文中,我们对定义4.3中的语义进行了扩展,以使用opt ∈ { max , min } \in\{\max , \min \} ∈{max,min}的argopt运算符的公式,包括 arg opt x a : e \arg \operatorname{opt}_{x} a: e argoptxa:e和 $\arg \operatorname{opt}{x{1}, x_{2}} a: e 直 观 地 , 直观地, 直观地,\arg \max _{x} a: e$在满足使算术公式a的值最大化的布尔公式e的那些中确定输入x。形式上,
- arg min x a : e \arg \min _{x} a: e argminxa:e在 T \mathcal{T} T 的求值返回输入 t ∈ T t \in \mathcal{T} t∈T ,使得 T ∣ = e [ x ↦ t ] \mathcal{T}|=e[x \mapsto t] T∣=e[x↦t] ,并且对于所有 t ′ ∈ T t^{\prime} \in \mathcal{T} t′∈T 使得 T ∣ = e [ x ↦ t ′ ] \mathcal{T}|=e\left[x \mapsto t^{\prime}\right] T∣=e[x↦t′],我们有 a [ x ↦ t ] ≤ a [ x ↦ t ′ ] a[x \mapsto t] \leq a\left[x \mapsto t^{\prime}\right] a[x↦t]≤a[x↦t′]。
启发法
我们提出了启发式δ,我们使用了第5节中讨论的覆盖要求。我们注意到,由于δ是一个启发式的,所以存在替代方案。下面的定义在我们的实验中工作得很好
7.1.1 Lipschitz连续性。当公式(10)中的李普希茨要求r不被T满足时,我们将其变换为δ®,如下所示:
arg
max
x
1
,
x
2
⋅
∥
v
[
x
1
]
1
−
v
[
x
2
]
1
∥
−
c
∗
∥
x
1
−
x
2
∥
:
x
1
,
x
2
∈
X
\arg \max _{x_{1}, x_{2}} \cdot\left\|v\left[x_{1}\right]_{1}-v\left[x_{2}\right]_{1}\right\|-c *\left\|x_{1}-x_{2}\right\|: x_{1}, x_{2} \in X
argx1,x2max⋅∥v[x1]1−v[x2]1∥−c∗∥x1−x2∥:x1,x2∈X
即,目标是在T中找到最佳t1和t2,以使||v[t1]1−v[t2]1||−c·||t1−t2||尽可能大。如上所述,我们还需要计算Val(t1,t2,r)=||v[t1]1−v[t2]1||−c·||t1−t2||
7.1.2神经元覆盖。当公式(11)中的需求r不被T满足时,我们将其转换为以下需求δ®:
arg
max
x
c
k
⋅
u
k
,
i
[
x
]
:
true
\arg \max _{x} c_{k} \cdot u_{k, i}[x]: \text { true }
argxmaxck⋅uk,i[x]: true
我们得到了具有最大值
c
k
⋅
u
k
,
i
[
x
]
c_{k} \cdot u_{k, i}[x]
ck⋅uk,i[x]的输入t∈T
系数Ck是每层常数。它的动机是下面的观察。随着信号在DNN中的传播,每一层的激活值可以具有不同的大小。例如,如果k层和k+1层神经元的最小激活值分别为−10和−100,则即使当神经元 u [ x ] k , i = − 1 > − 2 = u [ x ] k + 1 , j u[x]_{k, i}=-1>-2=u[x]_{k+1, j} u[x]k,i=−1>−2=u[x]k+1,j时,我们仍然可以认为 n k + 1 , j n_{k+1, j} nk+1,j比 n k , i n_{k, i} nk,i更接近被激活。因此,我们为每一层定义了一个层因子Ck,它将不同层神经元的平均激活值归一化到相同的幅度水平。它是通过对足够大的输入数据集进行采样来估计的。
7.1.3 SS Coverage。这是通过以下δ®实现的
arg
max
x
−
c
k
⋅
∣
u
[
x
]
k
,
i
∣
:
true
\arg \max _{x}-c_{k} \cdot\left|u[x]_{k, i}\right|: \text { true }
argxmax−ck⋅∣u[x]k,i∣: true
直观地,给定判定神经元
n
k
+
1
,
j
n_{k+1, j}
nk+1,j,等式(18)选择最接近激活符号变化的条件(即,产生最小的|u[x]k,i|)。
新的具体投入的符号化生成
本节介绍了算法1的第8行的方法,即给定一个具体的输入t和一个要求r,我们需要通过符号分析找到下一个具体的输入t‘。这个新的t‘将被添加到测试套件中(算法1的第10行)。要考虑的符号分析技术包括[23]中的线性规划,[21]中对L0范数的全局优化,以及下面将介绍的新的优化算法。我们将优化算法视为符号分析方法,因为与约束求解方法类似,它们在一次运行中处理一组测试用例。
为了简化演示,对于每个算法,下面的描述可能集中在一些特定的覆盖要求上,但我们要注意的是,所有算法都可以与第5节中给出的所有要求一起工作。
利用线性规划进行符号分析
如第4节所述,给定输入x,DNN实例N[x]映射到可以使用线性编程(LP)建模的激活模式AP[x]。具体地说,以下线性约束[23]产生表现出与x相同的RELU行为的一组输入:
{
u
k
,
i
=
∑
1
≤
j
≤
s
k
−
1
{
w
k
−
1
,
j
,
i
⋅
v
k
−
1
,
j
}
+
b
k
,
i
∣
k
∈
[
2
,
K
]
,
i
∈
[
1..
s
k
]
}
\left\{\mathbf{u}_{\mathbf{k}, \mathbf{i}}=\sum_{1 \leq j \leq s_{k-1}}\left\{w_{k-1, j, i} \cdot \mathbf{v}_{\mathbf{k}-1, j}\right\}+b_{k, i} | k \in[2, K], i \in\left[1 . . s_{k}\right]\right\}
⎩⎨⎧uk,i=1≤j≤sk−1∑{wk−1,j,i⋅vk−1,j}+bk,i∣k∈[2,K],i∈[1..sk]⎭⎬⎫
{ u k , i ≥ 0 ∧ u k , i = v k , i ∣ a p [ x ] k , i = true, k ∈ [ 2 , K ) , i ∈ [ 1.. s k ] } ∪ { u k , i < 0 ∧ v k , i = 0 ∣ a p [ x ] k , i = false, k ∈ [ 2 , K ) , i ∈ [ 1.. s k ] } \begin{array}{l} \left\{\mathbf{u}_{\mathbf{k}, \mathbf{i}} \geq 0 \wedge \mathbf{u}_{\mathbf{k}, \mathbf{i}}=\mathbf{v}_{\mathbf{k}, \mathbf{i}} | a p[x]_{k, i}=\text { true, } k \in[2, K), i \in\left[1 . . s_{k}\right]\right\} \\ \cup\left\{\mathbf{u}_{\mathbf{k}, \mathbf{i}}<0 \wedge \mathbf{v}_{\mathbf{k}, \mathbf{i}}=0 | a p[x]_{k, i}=\text { false, } k \in[2, K), i \in\left[1 . . s_{k}\right]\right\} \end{array} {uk,i≥0∧uk,i=vk,i∣ap[x]k,i= true, k∈[2,K),i∈[1..sk]}∪{uk,i<0∧vk,i=0∣ap[x]k,i= false, k∈[2,K),i∈[1..sk]}
线性规划模型中的连续变量用粗体强调。
- 每个神经元的激活值由(20)中的线性约束编码,这是计算神经元激活值的公式(2)的符号版本。
- 给定特定输入x,已知激活模式(定义4.1)AP[x]:AP[x]k,i为真或假,其指示REU对于神经元nk,i是否被激活,i。遵循(3)和(1)中REU的定义,对于每个神经元k,i,(21)中的线性约束编码REU激活(当AP[x]k,i=TRUE时)或去激活(当AP[x]k,i=FALSE时)
由(20)和(21)给出的线性模型(表示为C)表示导致与编码的激活模式相同的输入集合。因此,从输入和需求对(t,r)中寻找新输入的符号分析等价于寻找新的激活模式。注意,为了确保所获得的测试用例是有意义的,向LP模型添加了最小化t和t‘之间的距离的目标。因此,使用LP要求距离度量是线性的。例如,这适用于(6)中的L-∞-范数,但不适用于L2-范数。
8.1.1神经元覆盖率。神经元覆盖的符号分析取输入测试用例t和对神经元k的激活的要求r,i,并返回新的测试T‘,使得网络实例N[t’]满足测试要求。我们具有给定N[t]的激活模式AP[t],并且可以建立新的激活模式AP‘,从而
{
a
p
k
,
i
′
=
¬
a
p
[
t
]
k
,
i
∧
∀
k
1
<
k
:
⋀
0
≤
i
1
≤
s
k
1
a
p
k
1
,
i
1
′
=
a
p
[
t
]
k
1
,
i
1
}
\left\{a p_{k, i}^{\prime}=\neg a p[t]_{k, i} \wedge \forall k_{1}<k: \bigwedge_{0 \leq i_{1} \leq s_{k_{1}}} a p_{k_{1}, i_{1}}^{\prime}=a p[t]_{k_{1}, i_{1}}\right\}
⎩⎨⎧apk,i′=¬ap[t]k,i∧∀k1<k:0≤i1≤sk1⋀apk1,i1′=ap[t]k1,i1⎭⎬⎫
此激活模式指定以下条件。
- nk,i的激活符号被否定:这编码了激活nk,i的目标。
- 在新的激活模式Ap‘中,k层之前的神经元将其激活信号保留为ap[t]。尽管可能存在使Nk被激活的多个激活模式,但是对于LP建模的使用,必须预先确定激活信号的一个特定组合。
- 其他神经元是无关的,因为nk,i的符号只受前一层神经元激活值的影响
最后,LP模型C使用(20)和(21)对(22)中定义的新激活模式Ap‘进行编码,并且如果存在可行解,则可以从该解中提取满足要求r的新测试输入t’。
8.1.2 SS覆盖。为了满足SS覆盖要求r,我们需要找到一个新的测试用例,使得对于输入t,nk+1,j和nk,i的激活符号被否定,而层k处的其他神经元的其他符号等于输入t的那些符号。
为了实现这一点,构建了以下激活模式AP‘。
{
a
p
k
,
i
′
=
¬
a
p
[
t
]
k
,
i
∧
a
p
k
+
1
,
j
′
=
¬
a
p
[
t
]
k
+
1
,
j
∧
∀
k
1
<
k
:
A
p
k
1
,
i
1
′
=
a
p
[
t
]
k
1
,
i
1
}
\begin{aligned} \left\{a p_{k, i}^{\prime}=\neg a p[t]_{k, i} \wedge a p_{k+1, j}^{\prime}=\right.& \neg a p[t]_{k+1, j} \\ \wedge \forall k_{1}<k: &\left.A p_{k_{1}, i_{1}}^{\prime}=a p[t]_{k_{1}, i_{1}}\right\} \end{aligned}
{apk,i′=¬ap[t]k,i∧apk+1,j′=∧∀k1<k:¬ap[t]k+1,jApk1,i1′=ap[t]k1,i1}
8.1.3 神经元边界覆盖率。在神经元边界覆盖的情况下,符号分析的目的是找到一个输入t‘,使得神经元nk,i的激活值超过其上界hk,i或其下界lk,i。
为了实现这一点,在保留DNN激活模式AP[t]的同时,我们向LP程序添加了以下约束之一。
If
u
[
x
]
k
,
i
−
h
k
,
i
>
l
k
,
i
−
u
[
x
]
k
,
i
:
u
k
,
i
>
h
k
,
i
otherwise:
u
k
,
i
<
l
k
,
i
\begin{array}{l} \text { If } u[x]_{k, i}-h_{k, i}>l_{k, i}-u[x]_{k, i}: u_{k, i}>h_{k, i} \\ \text { otherwise: } u_{k, i}<l_{k, i} \end{array}
If u[x]k,i−hk,i>lk,i−u[x]k,i:uk,i>hk,i otherwise: uk,i<lk,i
基于全局优化的符号分析
寻找新输入的符号分析也可以通过求解[21]中的全局优化问题来实现。也就是说,通过将测试需求指定为优化目标,我们应用全局优化来计算满足测试覆盖需求的测试用例
-
对于神经元覆盖,目标是找到一个 t ′ t^{\prime} t′,使得指定的神经元 n k , i n_{k, i} nk,i有 a p [ t ′ ] k , i = a p\left[t^{\prime}\right]_{k, i}= ap[t′]k,i= true
-
在SS覆盖的情况下,给定神经元对 ( n k , i , n k + 1 , j ) \left(n_{k, i}, n_{k+1, j}\right) (nk,i,nk+1,j)和原始输入t,优化目标变为
a p [ t ′ ] k , i ≠ a p [ t ] k , i ∧ a p [ t ′ ] k + 1 , j ≠ a p [ t ] k + 1 , j ∧ ⋀ i ′ ≠ i a p [ t ′ ] k , i ′ = a p [ t ] k , i \begin{array}{l} a p\left[t^{\prime}\right]_{k, i} \neq a p[t]_{k, i} \wedge a p\left[t^{\prime}\right]_{k+1, j} \neq \\ a p[t]_{k+1, j} \wedge \bigwedge_{i^{\prime} \neq i} a p\left[t^{\prime}\right]_{k, i^{\prime}}=a p[t]_{k, i} \end{array} ap[t′]k,i=ap[t]k,i∧ap[t′]k+1,j=ap[t]k+1,j∧⋀i′=iap[t′]k,i′=ap[t]k,i -
对于神经元边界覆盖,根据激活 n k , i n_{k, i} nk,i的上界或下界,寻找新的输入t‘的目标是 u [ t ′ ] k , i > h k , i u\left[t^{\prime}\right]_{k, i}>h_{k, i} u[t′]k,i>hk,i or u [ t ′ ] k , i < l k , i u\left[t^{\prime}\right]_{k, i}<l_{k, i} u[t′]k,i<lk,i。
有关算法的详细信息,读者请参阅[21]。
Lipschitz测试用例生成
给定对子空间X的覆盖要求,如公式(10)所示,我们设
t
0
∈
R
n
t_{0} \in \mathbb{R}^{n}
t0∈Rn为t1和t2所属的子空间X的代表点。优化问题是生成两个输入t1和t2,使得
∥
v
[
t
1
]
1
−
v
[
t
2
]
1
∥
D
1
−
c
⋅
∥
t
1
−
t
2
∥
D
1
>
0
s.t.
∥
t
1
−
t
0
∥
D
2
≤
Δ
,
∥
t
2
−
t
0
∥
D
2
≤
Δ
\begin{array}{r} \left\|v\left[t_{1}\right]_{1}-v\left[t_{2}\right]_{1}\right\|_{D_{1}}-c \cdot\left\|t_{1}-t_{2}\right\|_{D_{1}}>0 \\ \text { s.t. }\left\|t_{1}-t_{0}\right\|_{D_{2}} \leq \Delta,\left\|t_{2}-t_{0}\right\|_{D_{2}} \leq \Delta \end{array}
∥v[t1]1−v[t2]1∥D1−c⋅∥t1−t2∥D1>0 s.t. ∥t1−t0∥D2≤Δ,∥t2−t0∥D2≤Δ
其中||∗||D1和||∗||D2表示范数度量,例如L0范数、L2范数或L∞范数,∆是范数球(对于L1和L2范数)的半径或以t0为中心的超立方体的大小(对于l∞范数)。常量∆是该算法的超参数。
提出了一种新颖的交替式罗盘搜索方案,有效地解决了上述问题。具体地说,我们通过松弛[19]交替解决以下两个优化问题,即最大化原始Lipschitz常数的下界,而不是直接最大化Lipschitz常数本身。为此,当范数||∗||D1和||∗||D2都是L-∞范数时,我们将原来的非线性比例优化重新表示为线性问题。
8.3.1第一阶段。我们解决
min
t
1
F
(
t
1
,
t
0
)
=
−
∣
∣
v
[
t
1
]
1
−
v
[
t
0
]
1
∥
D
1
s.t.
∥
t
1
−
t
0
∥
D
2
≤
Δ
\begin{aligned} \min _{t_{1}} F\left(t_{1}, t_{0}\right)=-|| v\left[t_{1}\right]_{1}-v\left[t_{0}\right]_{1} \|_{D_{1}} \\ & \text { s.t. }\left\|t_{1}-t_{0}\right\|_{D_{2}} \leq \Delta \end{aligned}
t1minF(t1,t0)=−∣∣v[t1]1−v[t0]1∥D1 s.t. ∥t1−t0∥D2≤Δ
如果方程(24)收敛,并且我们可以找到最优t1
t
1
∗
=
arg
min
t
1
F
(
t
1
,
t
0
)
s.t.
∥
t
1
−
t
0
∥
D
2
≤
Δ
t_{1}^{*}=\arg \min _{t_{1}} F\left(t_{1}, t_{0}\right) \text { s.t. }\left\|t_{1}-t_{0}\right\|_{D_{2}} \leq \Delta
t1∗=argt1minF(t1,t0) s.t. ∥t1−t0∥D2≤Δ
但是我们仍然找不到一个令人满意的输入对,我们执行第二阶段的优化。
8.3.2 第二阶段。我们解决
min
t
2
F
(
t
1
∗
,
t
2
)
=
−
∥
v
[
t
2
]
1
−
v
[
t
1
∗
]
1
∥
D
1
s.t.
∥
t
2
−
t
0
∥
D
2
≤
Δ
\begin{aligned} \min _{t_{2}} F\left(t_{1}^{*}, t_{2}\right)=-\left\|v\left[t_{2}\right]_{1}-v\left[t_{1}^{*}\right]_{1}\right\|_{D_{1}} & \\ & \text { s.t. }\left\|t_{2}-t_{0}\right\|_{D_{2}} \leq \Delta \end{aligned}
t2minF(t1∗,t2)=−∥v[t2]1−v[t1∗]1∥D1 s.t. ∥t2−t0∥D2≤Δ
8.3.3第三阶段。如果函数lip(t∗1,t∗2)在第二阶段没有取得进展,我们认为整个搜索过程是收敛的,并且没有找到能够驳斥给定Lipschitz常数c的输入对。在这种情况下,我们返回到目前为止找到的最佳输入对,即t∗1和t∗2,以及所观察到的最大Lipschitz常数Lip(t∗1,T2)。请注意,返回的常量小于c。
总之,该方法是一种基于指南针搜索的交替优化方案。基本上,我们从给定的t0开始在范数球或超立方体中搜索图像t1,其中范数球空间上的优化轨迹表示为S(t0,∆(T0)),使得lip(t0,t1)>c(此步骤是符号执行);如果找不到,则通过用t∗1(在此优化运行中找到的最佳具体输入)替换t0来修改优化目标函数,以启动空间上的另一优化轨迹,即S(t∗。重复这个过程,直到我们逐渐覆盖了范数球的整个空间S(∆(T0))。
这节略了一些
测试Oracle
我们详细介绍了对生成的测试输入执行的有效性检查(算法1的第9行),以及最终如何使用测试套件来量化DNN的安全性。
定义9.1(有效测试输入)。我们被给予输入的集合O,我们假设其具有正确的分类(例如,训练数据集)。给定实数b,如果满足以下条件,则测试输入t‘∈T被认为是有效的
∃
t
∈
O
:
∥
t
−
t
′
∥
≤
b
\exists t \in O:\left\|t-t^{\prime}\right\| \leq b
∃t∈O:∥t−t′∥≤b
直观地说,如果一个测试用例t接近我们有分类的一些输入,那么它就是有效的。给定测试输入t‘∈T,我们将O(t‘)写为O中所有输入t∈O中到t’的距离最小的输入t。
为了使用测试套件T来量化DNN的质量,我们使用以下健壮性标准。
定义9.2(健壮性Oracle)。给定分类输入的集合O,测试用例t‘通过健壮性预言,如果
arg
max
j
v
[
t
′
]
K
,
j
=
arg
max
j
v
[
O
(
t
′
)
]
K
,
j
\arg \max _{j} v\left[t^{\prime}\right]_{K, j}=\arg \max _{j} v\left[O\left(t^{\prime}\right)\right]_{K, j}
argjmaxv[t′]K,j=argjmaxv[O(t′)]K,j
只要我们发现一个测试输入没有通过这个预言,那么它就是DNN缺乏健壮性的证据。
实验结果
与DeepXplore的比较

图2:由DeepConcolic和DeepXplore生成的对抗性图像,具有用于MNIST(顶行)的L∞-Norm和用于CIFAR-10(底行)的L0-Norm,后者具有图像约束“光”、“遮挡”和“暗”。
现在,我们在从MNIST和CIFAR-10数据集获得的DNN上比较DeepConcolic和DeepXplore[18]。我们注意到DeepXplore已经应用于更多的数据集。
对于每个工具,我们从随机采样的图像输入开始神经元覆盖测试。请注意,由于DeepXplore需要多个DNN,因此我们将经过训练的DNN指定为目标模型,并使用DeepXplore提供的另外两个默认模型。表2给出了这两个工具获得的神经元覆盖率。我们观察到,在DeepConcolic的三种操作模式(“亮”、“遮挡”和“熄灭”)中,DeepConcolic产生的神经元覆盖率比DeepXplore高得多。另一方面,DeepXplore的速度要快得多,并且在几秒钟内终止。
图2给出了DeepConcolic(具有L∞范数和L0范数)和DeepXplore发现的几个对抗性示例。虽然DeepConcolic不像DeepXplore那样对原始图像施加特定领域的约束,但Concolic测试生成的图像类似于“人类感知”。例如,基于L∞范数,它生成逐渐反转黑白颜色的对抗性示例(图2,顶行)。对于L0范数,DeepConcolic生成类似于DeepXplore在“中断”约束下的对抗性示例,这本质上是像素操作
NC、SCC和NBC的结果
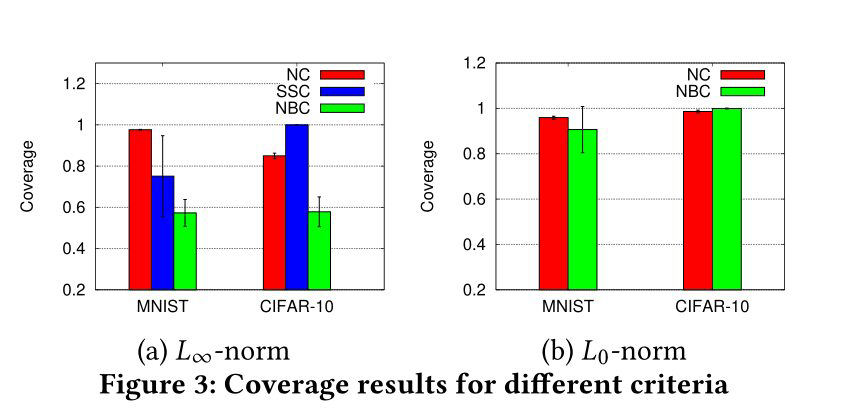
我们给出了使用覆盖标准NC、SSC和NBC使用DeepConcolic获得的结果。DeepConcolic使用单个种子输入开始NC测试。对于SSC和NBC,为了提高性能,将对初始的1000幅图像进行采样。此外,我们只测试SSC和NBC神经元的一个子集。建立了0.3(L∞范数)和10 0像素(L0范数)的距离上界,用于收集对抗性实例。
完整的覆盖报告,包括平均覆盖和标准推导,如图3所示。表3包含对抗性示例结果。我们观察到,使用全局优化进行符号分析的开销太高(第8.2节)。因此,具有L0范数的SSC结果被排除在外。
总体而言,DeepConcolic实现了高覆盖率,并使用健壮性检查(定义9.2)检测到大量的对抗性示例。然而,角例激活值(即,NBC)的覆盖范围是有限的
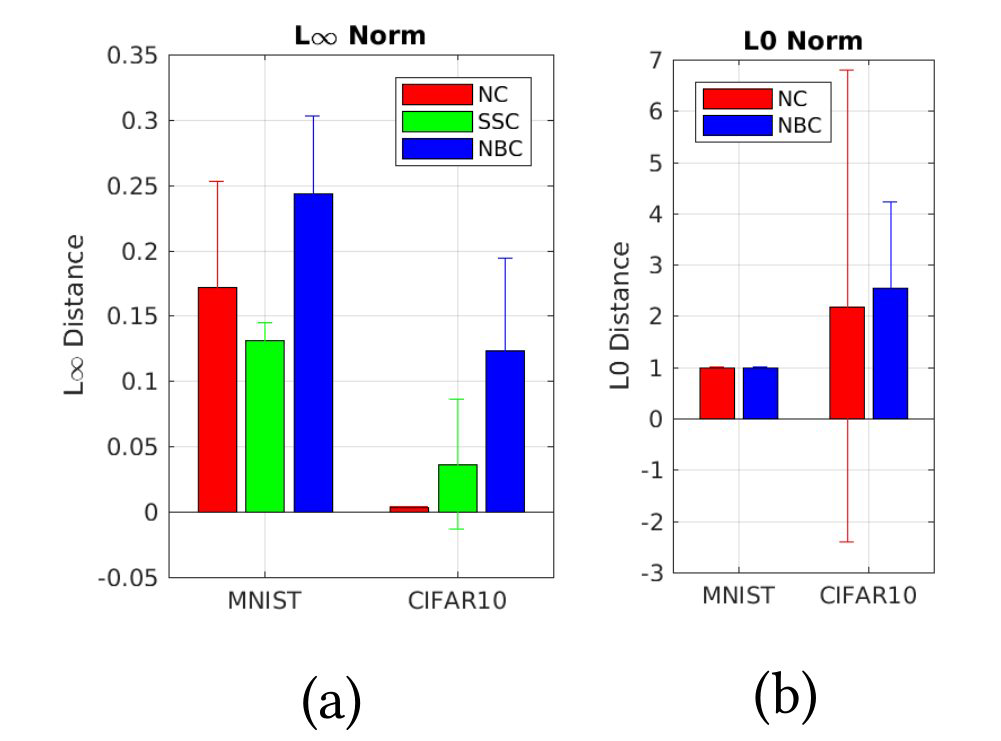
Concolic测试能够找到具有最小可能距离的对抗性示例:即,1255≈0.0039用于L∞范数,1像素用于L0范数。图4给出了对抗性示例的平均距离(来自一次DeepConcolic运行)。值得注意的是,对于同一网络,当距离度量改变时,使用NC发现的对抗性示例的数量可能会有很大变化。这一观察结果表明,在设计DNN的覆盖标准时,需要使用各种距离度量来检查它们。
关于Lipschitz常数检验的结果
10.3.1基线方法。由于本文首次测试了DNN的Lipschitz常数,因此我们将我们的方法与随机测试用例生成方法进行了比较。对于这个特定的测试要求,给定预定义的Lipschitz常数c、输入t0和范数球(例如,对于L1和L2范数)或超立方体空间(对于L∞-范数)∆的半径,我们随机生成满足空间约束的两个测试对t1和t2(即,||t1−t0||d2≤∆和||t2−t0||d2≤∆),然后检查lip(t1,t2)>c是否成立。我们重复随机生成,直到找到令人满意的测试对或重复次数大于预定义的阈值。我们设定了这样的门槛,即Nr_d=1,000,000。也就是说,如果我们随机生成1,000,000个测试对,并且它们都不能满足Lipschitz常数要求>c,则我们将此测试视为失败,并返回找到的最大Lipschitz常数和相应的测试对;否则,我们将其视为成功,并返回满意的测试对。
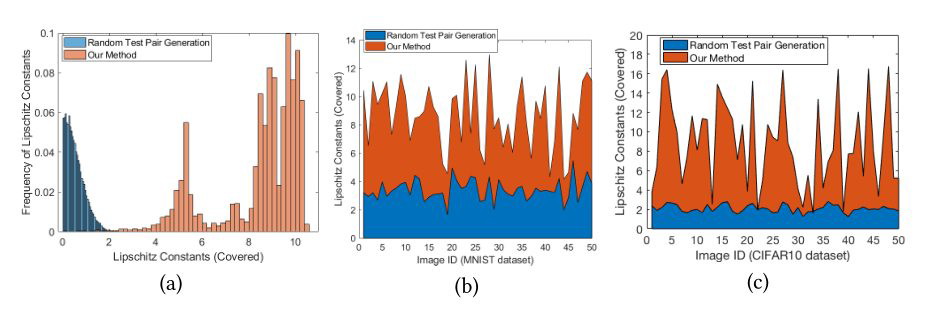
10.3.2实验结果。图5(A)描述了由1,000,000个随机测试对生成的Lipschitz常数覆盖,以及我们在MNIST
DNN上为image-1生成的Concolic测试生成方法。正如我们所看到的,即使我们通过随机测试生成的方式产生了100万个测试对,但最大Lipschitz转换率只达到了3.23,并且大多数测试对都在[0.01,2]的范围内。另一方面,我们的Concolic方法可以覆盖[0.01,10.38]的Lipschitz范围,其中大多数情况位于[3.5,10],而随机测试生成很难覆盖这一范围。
图5(B)和©比较了MNIST和CIFAR-10模型上随机方法和Concolic方法测试对的Lipschitz常数覆盖率。我们的方法的性能明显优于随机测试用例生成。我们注意到,覆盖DNNs的较大Lipschitz常数范围是一个具有挑战性的问题,因为大多数图像对(在某个高维空间内)都可以产生较小的Lipschitz常数(如1到2)。这就解释了为什么随机生成的测试对集中在小于3的范围内。然而,对于自动驾驶汽车等安全关键应用,Lipschitz常数较大的DNN本质上表明它更容易受到对手的扰动[20,21]。因此,可以覆盖较大Lipschitz常数的测试方法为训练的DNN提供了有用的鲁棒性指标。我们认为,对于DNNs的安全测试,Lipschitz常数覆盖的Concolic测试方法可以补充现有的方法来实现更好的覆盖。
结论
在本文中,我们提出了第一种DNNs的Concolic测试方法。我们在一个软件工具中实现了该工具,并将该工具应用于评估知名DNN的健壮性。测试输入的生成可以由包括Lipschitz连续性在内的各种覆盖度量来指导。我们的实验结果证实,具体执行和符号分析的结合既提供了覆盖率,又自动发现了对抗性示例。





 本文提出了一种针对深度神经网络(DNNs)的符号测试方法,通过结合具体执行和符号分析来探索DNN的执行路径,提高了测试覆盖率并自动发现了大量对抗性实例。该方法在软件工具DeepConcolic中实现,实验结果表明,Concolic测试在获取高覆盖率和发现对抗性实例方面是有效的。
本文提出了一种针对深度神经网络(DNNs)的符号测试方法,通过结合具体执行和符号分析来探索DNN的执行路径,提高了测试覆盖率并自动发现了大量对抗性实例。该方法在软件工具DeepConcolic中实现,实验结果表明,Concolic测试在获取高覆盖率和发现对抗性实例方面是有效的。
















 2510
2510

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








