题目链接:[HAOI2011]Problem b
妈妈我终于会反演啦【雾
其实我就是来码个公式复习一下QwQ
前置技能:
那么按照题意,我们令
首先明确我们为什么要反演,因为我们要求一个不好直接算的东西,而他和一个容易计算的东西有关系,所以我们要同过那个容易计算的东西来反向计算出我们真正要求的东西
于是我们令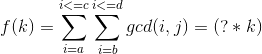
根据前置技能得
这时候发现d/k求起来很麻烦,换个元,令d'=d/k
于是
再来化简f函数得到
所以
所以
然后分块求就好了,线性筛出莫比乌斯函数并求出前缀和,注意容斥一下
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
const int maxn=100010;
int a,b,c,d,k;
int p[maxn],N=0,mu[maxn];
bool vis[maxn];
void get_pre(){
mu[1]=1;
for (int i=2;i<=maxn-5;++i){
if (!vis[i]){
p[++N]=i;
mu[i]=-1;
}
for (int j=1;j<=N&&p[j]*i<=maxn-5;++j){
vis[p[j]*i]=1;
if (i%p[j]==0){mu[p[j]*i]=0;break;}
mu[p[j]*i]=-mu[i];
}
}
for (int i=2;i<=maxn;++i) mu[i]+=mu[i-1];
}
LL solve(int l,int r){
int last; LL ret=0;
l/=k; r/=k;
for (int i=1;i<=l&&i<=r;i=last+1){
last=min(l/(l/i),r/(r/i));
ret+=1LL*(l/i)*(r/i)*(mu[last]-mu[i-1]);
}return ret;
}
int main(){
get_pre(); int T; scanf("%d",&T);
while (T--){
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
printf("%lld\n",solve(b,d)-solve(a-1,d)-solve(b,c-1)+solve(a-1,c-1));
}
}










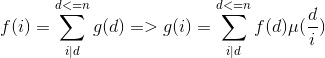

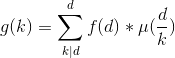
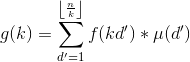
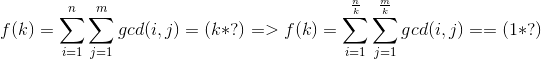
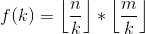
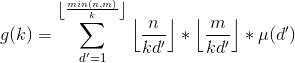














 347
347

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








