本文详细介绍了CCMboost转换器的建模过程，包括平均模型和交流小信号模型的建立，并探讨了右半平面零点（RHPZ）对系统性能的影响。通过KCL和KVL推导出传递函数，分析了占空比变化对输出电压瞬态响应的影响，揭示了RHPZ如何导致相位裕量恶化。
CCM boost建模和右半平面零点（RHPZ）
CCM DC-DC建模流程
经过上次buck建模，感觉这种方法还是比较方便直观的。
-
用受控源代替开关和二极管，获得平均模型
-
开关：求电流的开关周期平均，等效为受控电流源
-
二极管：求电压的开关周期平均，等效为受控电压源
-
-
受控源存在耦合项（比如占空比和电感电流
D(t)*iL(t)），进行全微分后，分解成多个线性的受控源，获得交流小信号模型 -
根据交流小信号模型
- 通过KCL和KVL，获得各个传递函数：输入到输出、控制（占空比）到输出
- 通过仿真，获得开环波特图
这次再以CCM boost为例，主要看下传递函数怎么写。
平均模型
模型
把MOS电流和二极管电压做开关周期平均：
（包含了二极管的正向压降Vd，假设为恒定值）
i
M
O
S
=
D
(
t
)
i
L
(
t
)
v
d
i
o
d
e
=
−
D
(
t
)
V
o
(
t
)
+
(
1
−
D
)
V
d
i_{MOS} = D(t)i_L(t) \\ v_{diode} = -D(t)V_o(t) + (1-D)V_d
iMOS=D(t)iL(t)vdiode=−D(t)Vo(t)+(1−D)Vd
对应的模型：
验证
输入电压跳变时，开关模型和平均模型的电感电流和输出电压的暂态过程基本一致。
交流小信号模型
模型
受控源存在耦合项，进行全微分后，分解成多个线性的受控源，获得交流小信号模型
Δ
i
M
O
S
=
D
Δ
i
L
(
t
)
+
I
L
Δ
d
(
t
)
Δ
v
d
i
o
d
e
=
−
(
V
o
−
V
d
)
Δ
d
(
t
)
−
D
Δ
v
o
(
t
)
\Delta i_{MOS} = D\Delta i_L(t) + I_L \Delta d(t) \\ \Delta v_{diode} = -(V_o-V_d) \Delta d(t) - D\Delta v_o(t)
ΔiMOS=DΔiL(t)+ILΔd(t)Δvdiode=−(Vo−Vd)Δd(t)−DΔvo(t)
其中，考虑二极管压降Vd，输出电压和电感电流为，
V
o
=
V
i
1
−
D
−
V
d
I
L
=
I
o
1
−
D
=
V
o
R
L
(
1
−
D
)
V_o = \frac{V_i}{1-D}-V_d \\ I_L = \frac{I_o}{1-D} = \frac{V_o}{R_L(1-D)}
Vo=1−DVi−VdIL=1−DIo=RL(1−D)Vo
模型为：
验证
占空比只能变化很小范围（例如10%以内），范围变大就不准确了。
例如，占空比在0.3和0.33之间跳变。开关模型和交流小信号模型的电感电流对比。
尝试减去直流偏置后，形状是基本一致的。
传递函数
基于交流小信号模型，用KVL和KCL写电感和电容的方程（s域）：
s
L
i
L
(
s
)
=
v
i
(
s
)
−
(
1
−
D
)
v
o
(
s
)
+
(
V
o
+
V
d
)
d
(
s
)
s
C
v
o
(
s
)
=
(
1
−
D
)
i
L
(
s
)
−
I
L
d
(
s
)
−
v
o
(
s
)
/
R
sLi_L(s) = v_i(s) - (1-D)v_o(s) + (V_o+V_d)d(s) \\ sCv_o(s) = (1-D)i_L(s) - I_L d(s) - v_o(s) / R
sLiL(s)=vi(s)−(1−D)vo(s)+(Vo+Vd)d(s)sCvo(s)=(1−D)iL(s)−ILd(s)−vo(s)/R
例如，求控制到输出的传递函数
v
o
(
s
)
/
d
(
s
)
v_o(s)/d(s)
vo(s)/d(s)时，令
v
i
(
s
)
=
0
v_i(s)=0
vi(s)=0，消去
i
L
(
s
)
i_L(s)
iL(s)：
v o ( s ) d ( s ) = ( V o + V d ) ( 1 − D ) − I L L s L C s 2 + L R s + ( 1 − D ) 2 = V i − I L L s L C s 2 + L R s + ( 1 − D ) 2 \frac{v_o(s)}{d(s)}=\frac{(V_o+V_d)(1-D)-I_L Ls}{LCs^2+\frac{L}{R}s+(1-D)^2}=\frac{V_i-I_L Ls}{LCs^2+\frac{L}{R}s+(1-D)^2} d(s)vo(s)=LCs2+RLs+(1−D)2(Vo+Vd)(1−D)−ILLs=LCs2+RLs+(1−D)2Vi−ILLs
其中，根据之前的结果，输出电压和电感电流为：
V
o
=
V
i
1
−
D
−
V
d
I
L
=
I
o
1
−
D
=
V
o
R
L
(
1
−
D
)
=
V
i
−
(
1
−
D
)
V
d
R
L
(
1
−
D
)
2
V_o = \frac{V_i}{1-D}-V_d \\ I_L = \frac{I_o}{1-D} = \frac{V_o}{R_L(1-D)} = \frac{V_i-(1-D)V_d}{R_L(1-D)^2}
Vo=1−DVi−VdIL=1−DIo=RL(1−D)Vo=RL(1−D)2Vi−(1−D)Vd
代入后，
v o ( s ) d ( s ) = ( V o + V d ) ( 1 − D ) − I L L s L C s 2 + L R s + ( 1 − D ) 2 = V i − V i − ( 1 − D ) V d R ( 1 − D ) 2 L s L C s 2 + L R s + ( 1 − D ) 2 \frac{v_o(s)}{d(s)}=\frac{(V_o+V_d)(1-D)-I_L Ls}{LCs^2+\frac{L}{R}s+(1-D)^2}=\frac{V_i-\frac{V_i-(1-D)V_d}{R(1-D)^2}Ls}{LCs^2+\frac{L}{R}s+(1-D)^2} d(s)vo(s)=LCs2+RLs+(1−D)2(Vo+Vd)(1−D)−ILLs=LCs2+RLs+(1−D)2Vi−R(1−D)2Vi−(1−D)VdLs
如果忽略二极管压降
V
d
=
0
V_d=0
Vd=0，理想情况下的控制到输出传递函数：
v
o
(
s
)
d
(
s
)
=
(
V
o
+
V
d
)
(
1
−
D
)
−
I
L
L
s
L
C
s
2
+
L
R
s
+
(
1
−
D
)
2
=
V
i
(
1
−
1
R
(
1
−
D
)
2
L
s
)
L
C
s
2
+
L
R
s
+
(
1
−
D
)
2
\frac{v_o(s)}{d(s)}=\frac{(V_o+V_d)(1-D)-I_L Ls}{LCs^2+\frac{L}{R}s+(1-D)^2}=\frac{V_i\left(1-\frac{1}{R(1-D)^2}Ls \right)}{LCs^2+\frac{L}{R}s+(1-D)^2}
d(s)vo(s)=LCs2+RLs+(1−D)2(Vo+Vd)(1−D)−ILLs=LCs2+RLs+(1−D)2Vi(1−R(1−D)21Ls)
可以看到传递函数有一个右半平面零点 s = R ( 1 − D ) 2 L s=\frac{R(1-D)^2}{L} s=LR(1−D)2。
右半平面零点（RHPZ）
右半平面零点Right Half Plane Zero (RHPZ)。RHPZ的幅频特性与一般的左半平面零点相同，但是相频特性与极点相同，给系统引入了-90°相位，恶化了相位裕量。一般开环增益的穿越频率需要设置为小于RHPZ所在频率。
对这篇博文中搭建的boost模型，在占空比较大时更容易观察到这个现象。比如占空比在0.5和0.55跳变：
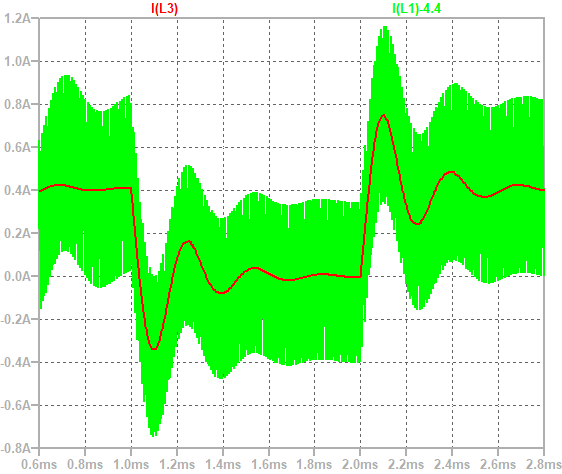
从boost二极管电流的角度直观理解一下这个现象。看D从0.8突变到0.5的情况，电阻负载。
- D=0.8时，输出电压高，电感电流I(L1)和负载电流都较大。
- D突变为0.5时，理论输出电压低于D=0.8的情况，因此最终电感电流和负载电流都会减小。
- 电感电流需要一定时间下降，而在这段时间里，因为(1-D)从0.2增大为0.5，实际上流过二极管的电流反而增大了，给输出电容充电，电压上升。因此在这段时间内，输出电压会先上升，再下降。
类似的RHPZ现象发生在变比与(1-D)有关的变换器中（或者说，在开关断开期间向输出侧传输能量），如buck-boost、flyback等。
扫一扫
461
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
