1 , 正态分布 :
- 公式 :
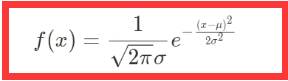
- 图 :

- 意义 :
μ : 平均数
derta : 标准差
2 ,期望 :
- 射手打中几环的概率 :

- 期望 : 假设打 100 次,他大概能射中的平均分数是多少 ?

- 总结 :
期望 = 求和(次数i × 概率i) / 总次数 - 期望是否等于平均数 : 正态分布等于,非正态分布不等于

3 ,方差 : ( 数据 - 期望 )^2 的加和
- 意义 : 数据的波动强度
- 例子 : 甲乙两个车间生产零件,产生次品的概率如下

- 问 : 各自生产 1000 件商品,平均次品数,方差,哪个车间的产品质量好
1 ,甲次品数,期望 : E(X) = 加和 ( 数量 × 概率 ) = 1.7
2 ,乙次品数,期望 : E(Y) = 1.7 - 分析 : 期望一样,那就求方差,看他的波动
- 求方差 : ( 数据 - 期望 )^2

- 哪个质量好 :
方差小的比较稳定,所以 : 乙厂质量更好




 本文深入解析正态分布的公式与意义,探讨期望与方差的概念,并通过实例对比两个车间的产品质量,揭示方差在衡量数据稳定性中的关键作用。
本文深入解析正态分布的公式与意义,探讨期望与方差的概念,并通过实例对比两个车间的产品质量,揭示方差在衡量数据稳定性中的关键作用。
















 5475
5475

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








