hdu 3070 Fibonacci && poj 1575 Tr A（矩阵快速幂模板题）

Fibonacci

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 13637		Accepted: 9669

Description

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, and F_n = F_{n − 1} + F_{n − 2} for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

Given an integer n, your goal is to compute the last 4 digits of F_n.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of F_n. If the last four digits of F_n are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print F_n mod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

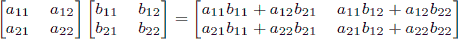Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int MOD = 1e4;
struct node
{
    int matrix[2][2];
    node() {}
    node(int a, int b, int c, int d)
    {
        matrix[0][0] = a;
        matrix[0][1] = b;
        matrix[1][0] = c;
        matrix[1][1] = d;
    }
};
node mul(node p, node q)
{
    node t = node(0, 0, 0, 0);
    for(int i = 0; i < 2; i++)
        for(int j = 0; j < 2; j++)
            for(int k = 0; k < 2; k++)
            t.matrix[i][j] = (t.matrix[i][j] + p.matrix[i][k] * q.matrix[k][j]) % MOD;
    return t;
}
node quick_matrix(node p, int n)
{
    node q = node(1, 0, 0, 1);
    while(n)
    {
        if(n & 1) q = mul(p,q);
        p = mul(p, p);
        n >>= 1;
    }
    return q;
}
int main()
{
    int n;
    node p;
    while(scanf("%d", &n), n+1)
    {
        p = node(1, 1, 1, 0);
        if(n == 0) {printf("0\n" ); continue;}
        p = quick_matrix(p, n-1);
        printf("%d\n", p.matrix[0][0]);
    }
    return 0;
}

Tr A

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4458    Accepted Submission(s): 3355

Problem Description

A为一个方阵，则Tr A表示A的迹（就是主对角线上各项的和），现要求Tr(A^k)%9973。

 

Input

数据的第一行是一个T，表示有T组数据。
每组数据的第一行有n(2 <= n <= 10)和k(2 <= k < 10^9)两个数据。接下来有n行，每行有n个数据，每个数据的范围是[0,9]，表示方阵A的内容。

 

Output

对应每组数据，输出Tr(A^k)%9973。

 

Sample Input

  
  

   
   2
2 2
1 0
0 1
3 99999999
1 2 3
4 5 6
7 8 9
  
  

 

Sample Output

  
  

   
   2
2686
  
  

 

Author

xhd

#include <iostream>
#include <cstdio>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MOD = 9973;
int n;
struct node
{
    int matrix[15][15];
};
node mul(node p, node q)
{
    node t;
    memset(t.matrix, 0, sizeof(t.matrix));
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
            for(int k = 0; k < n; k++)
            t.matrix[i][j] = (t.matrix[i][j] + p.matrix[i][k] * q.matrix[k][j]) % MOD;
    return t;
}
node quick_matrix(node p, int k)
{
    node q;
    memset(q.matrix, 0, sizeof(q.matrix));  //在栈里定义数组一定要清空下，因为他不会初始赋值0
    for(int i = 0; i < n; i++)
        q.matrix[i][i] = 1;
    while(k)
    {
        if(k & 1) q = mul(p,q);
        p = mul(p, p);
        k >>= 1;
    }
    return q;
}
int main()
{
    int t, k;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d%d", &n, &k);
        node p;
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                scanf("%d", &p.matrix[i][j]);
        p = quick_matrix(p, k);
        int ans = 0;
        for(int i = 0; i < n; i++)
            ans = (ans + p.matrix[i][i]) % MOD;
        printf("%d\n" ,ans);
    }
    return 0;
}