数据结构笔记--1.1.3关于算法效率 计算多项式值

秦九韶算法

• f(x)=a[n]x^n+a[n-1]x^(n-1)+…+a[1]x+a[0]
• f(x)=(…((a[n]x+a[n-1])x+a[n-2])x+…+a[1])x+a[0]. 　

---

clock() 计时函数的用法

#include "stdafx.h"
#include <iostream>
#include <time.h>

clock_t start, stop;
double duration;

int main()
{
    start = clock();
    //myfunction();
    stop = clock();
    duration = ((double)(stop - start)) / CLK_TCK;
    std::cout<<duration;
    return 0;
}

---

普通方法和秦九韶算法

#include "stdafx.h"
#include <iostream>
#include <time.h>
#include <math.h>
#define MAXK 1e7 //被测函数最大重复调用次数10的7次方
#define MAXN 10
double f1(int n, double a[], double x);
double f2(int n, double a[], double x);
clock_t start, stop;
double duration = 0.0;

double f1(int n, double a[], double x)
{
    int i;
    double p = a[0];
    for (i = 1;i <=n;i++)
        p += (a[i] * pow(x, i));
    //std::cout << p;
    //std::cout << std::endl;
    return p;
}

double f2(int n, double a[], double x)
{
    int i;
    double p = a[n];
    for (i = n;i > 0;i--)
        p = a[i-1] + p*x;//i-1
    //std::cout << p;
    //std::cout << std::endl;
    return p;
}

int main()
{
    int i;
    double a[MAXN];
    for (i = 0;i < MAXN;i++)
        a[i] = (double)i;

    start = clock();
    //myfunction();
    for (i = 0;i < MAXK;i++)
        f1(MAXN - 1, a, 1.1);
    stop = clock();
    duration = ((double)(stop - start)) / CLK_TCK/MAXK;
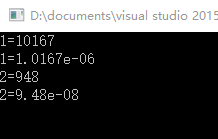
    std::cout << "1=" << ((double)(stop - start));
    std::cout << std::endl;
    std::cout <<"1="<< duration;
    std::cout << std::endl;

    start = clock();
    //myfunction();
    for (i = 0;i < MAXK;i++)
        f2(MAXN - 1, a, 1.1);
    stop = clock();
    duration = ((double)(stop - start)) / CLK_TCK/MAXK;
    std::cout << "2=" << ((double)(stop - start));
    std::cout << std::endl;
    std::cout << "2="<<duration;
    return 0;
}

相差大约一个数量级