二分图匹配的一点说明

       看了看网上的博客，没几篇讲得好的，介于我自己也无法描述清楚，就凑合看看吧。

      （以下源自百度百科）

       二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

       简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。

       无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。

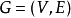
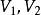
       设是一个无向图。如顶点集V可分割为两个互不相交的子集，选择这样的子集中边数最大的子集称为图的最大匹配问题（maximal matching problem)。

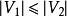
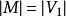
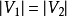
       如果一个匹配中，且匹配数，则称此匹配为完全匹配，也称作完备匹配。特别的当称为完美匹配。

       在介绍匈牙利算法之前还是先提一下几个概念，下面M是G的一个匹配。

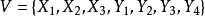
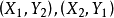
       若，，其中边已经在匹配M上。

       M-交错路：p是G的一条通路，如果p中的边为属于M中的边与不属于M但属于G中的边交替出现，则称p是一条M-交错路。如：路径 ，。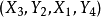

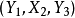
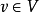
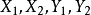
       M-饱和点：对于，如果v与M中的某条边关联，则称v是M-饱和点，否则称v是非M-饱和点。如都属于M-饱和点，而其它点都属于非M-饱和点。

       M-可增广路：p是一条M-交错路，如果p的起点和终点都是非M-饱和点，则称p为M-可增广路。如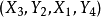（不要和流网络中的增广路径弄混了）。

       求最大匹配的一种显而易见的算法是：先找出全部匹配，然后保留匹配数最多的。但是这个算法的时间复杂度为边数的指数级函数。因此，需要寻求一种更加高效的算法。下面介绍用增广路求最大匹配的方法（称作匈牙利算法，匈牙利数学家Edmonds于1965年提出）。

       增广路的定义（也称增广轨或交错轨）：

       若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边（即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。

       由增广路的定义可以推出下述三个结论：

       （1）P的路径个数必定为奇数，第一条边和最后一条边都不属于M。

       （2）将M和P进行取反操作可以得到一个更大的匹配。

       （3）M为G的最大匹配当且仅当不存在M的增广路径。

       算法轮廓：

       （1）置M为空

       （2）找出一条增广路径P，通过异或操作获得更大的匹配代替M

       （3）重复（2）操作直到找不出增广路径为止

       如果不懂可以看这篇博客。

       我还是比较适合讲题目，那么看看HDU2063。裸的匈牙利算法模板题。

Code：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#define N 1005
using namespace std;
int flag[N][N],girl[N],used[N],n,k,m;
bool found(int x)
{
	for(int i=1;i<=n;i++)
		if(flag[x][i]&&!used[i])
		{
			used[i]=1;
			if(girl[i]==0||found(girl[i]))
			{
				girl[i]=x;
				return 1;
			}
		}
	return 0;
}
int main()
{
	scanf("%d",&k);
	while(k)
	{
		scanf("%d%d",&m,&n);
		memset(flag,false,sizeof(flag));
		memset(girl,0,sizeof(girl));
		for(int i=1;i<=k;i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			if(x>m||y>n)continue;
			flag[x][y]=true;
		}
		int ans=0;
		for(int i=1;i<=m;i++)
		{
			memset(used,0,sizeof(used));
			if(found(i))ans++;
		}
		printf("%d\n",ans);
		scanf("%d",&k);
	}
}

       下面讲一下二分图匹配的相关定理（不会证明，我的证明都是借鉴各位大神的）。

       1、二分图中最小顶点覆盖等于最大匹配数

       最小顶点覆盖：实质是个点集，点集里面的点能覆盖所有的边，最小顶点覆盖就是满足这个要求的点集中点数最小的那个。

       证明：首先，最小顶点覆盖一定>=最大匹配，因为假设最大匹配为n，那么我们就得到了n条互不相邻的边，光覆盖这些边就要用到n个点。这里事实上就可以看出最小顶点覆盖和最大匹配的不同了，最大匹配的点一定是两两成对的，而最小顶点覆盖还有相对孤立的点。注意是相对孤立，并不是他们之间肯定没有边，而是不属于匹配范围内的。那么匹配范围外的节点，一种就是有边和匹配范围内元素相连但是没有匹配到，一种就是没边。

       有边的话这个边就连在了匹配范围内，那这个顶点覆盖代表元素就是既可以连接上匹配元素，又可以连接到非匹配元素，相当于这个非匹配范围内的元素被这个“特殊顶点”覆盖，最小顶点覆盖数并没有增加；

       那么完全没边的孤立节点呢？好嘞，最小点集覆盖目的就是要覆盖所有的边，既然这个节点没有边相连，那还要你干毛？滚吧。这样依然没有影响最小顶点覆盖数。

       至此，匹配范围外的所有节点都不可能影响到最小顶点覆盖数，所以两者完全相等。

       2、二分图中最小边覆盖=顶点数-最小顶点覆盖（最大匹配）

最小边覆盖：实质是个边集，这个集合里的边能覆盖所有的点，最小边覆盖是满足这个要求的所有边集中边数最少的一个。

       这里顶点数等于总的顶点数，是二分图两边的顶点数，不是一边。

       证明：设最大匹配数为m，总顶点数为n。为了使边数最少，又因为一条边最多能干掉两个点，所以尽量用边干掉两个点。也就是取有匹配的那些边，当然这些边是越多越好，那就是最大匹配了，所以先用最大匹配数目的边干掉大多数点。剩下的解决没有被匹配的点，就只能一条边干掉一个点了，设这些数目为a，显然，2m+a=n，而最小边覆盖=m+a，所以最小边覆盖=（2m+a）-m=n-m。

       3、二分图中最大独立集+最小顶点覆盖（最大匹配）=顶点数

       最大独立集：实质是个点集，这个集合里的点无论怎样都两两相连不到一起，满足这个要求的点数最少的一个。

       证明：这个最好理解了，既然最小顶点覆盖就是最大匹配的那些顶点，那么剩下的节点就是相对孤立的点。而这些相对孤立的点两两肯定没有边(若有边，匹配数就该加一了，也就是这两点是匹配点)，不就是最大独立集吗？那这样所有的点就都考虑到了，两者一加就变成了所有顶点数。