机器学习笔记之高斯分布(三)——从几何角度观察多维高斯分布

引言

回顾：一维高斯分布

在使用极大似然估计计算高斯分布最优参数一节中介绍了一维高斯分布。具体表示如下：
$$x\sim \mathcal{N}(\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left\{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right\}$$

其中$x,\mu ,\sigma$均属于一维矩阵，即标量。

多维高斯分布

多维高斯分布与一维高斯分布的明显区别是：随机变量$x$，期望$\mu$以多维向量的形式出现，方差以多维矩阵的形式出现(方阵)。
随机变量定义：
数据集合$\mathcal{X}$包含$N$个样本：
$$\mathcal{X}=\left\{x^{(1)},x^{(2)},\cdots ,x^{(N)}\right\}$$
其中，$\mathcal{X}$中 任意样本 x ( i ) ( i ∈ { 1 , 2 , ⋯   , N } ) x^{(i)}(i \in \{1,2,\cdots,N\}) x(i)(i∈{1,2,⋯,N})均属于$p$维随机变量，记作$x^{(i)}\in {\mathbb{R}}^p$；
以样本$x^{(i)}$为例，其向量表示如下：
$$x^{(i)}={\left(x_1^{(i)},x_2^{(i)},\cdots ,x_p^{(i)}\right)}_{p\times 1}^T$$
期望$\mu$同样属于$p$维随机变量。每一维度值表示数据集合中所有样本对应该维度值的期望结果。$\mu$的向量表示如下：
$$\mu =({\mu }_1,{\mu }_2,\cdots ,{\mu }_p)$$

$\Sigma$表示协方差矩阵。它的定义表示如下：
$x$表示‘宏观意义’上的样本;任意样本。
$$\Sigma =\mathbb{E}[(x-\mu )(x-\mu {)}^T]$$
由于多维高斯分布中$x,\mu$均为$p$维向量。因此，将$x=(x_1,x_2,\cdots ,x_p),\mu =({\mu }_1,{\mu }_2,\cdots ,{\mu }_p)$带入上式：
$$\Sigma =\mathbb{E}\left[\begin{array}{c}(x_1-{\mu }_1{)}^2,(x_1-{\mu }_1)(x_2-{\mu }_2),\cdots ,(x_1-{\mu }_1)(x_p-{\mu }_p)\\ (x_2-{\mu }_2)(x_1-{\mu }_1),(x_2-{\mu }_2{)}^2,\cdots ,(x_2-{\mu }_2)(x_p-{\mu }_p)\\ ⋮\\ (x_p-{\mu }_p)(x_1-{\mu }_1),(x_p-{\mu }_p)(x_2-{\mu }_2),\cdots ,(x_p-{\mu }_p{)}^2\end{array}\right]={\left(\begin{array}{c}{\sigma }_{11},{\sigma }_{12},\cdots ,{\sigma }_{1p}\\ {\sigma }_{21},{\sigma }_{22},\cdots ,{\sigma }_{2p}\\ ⋮\\ {\sigma }_{p1},{\sigma }_{p2},\cdots ,{\sigma }_{pp}\end{array}\right)}_{p\times p}$$
观察上述矩阵，发现${\sigma }_{ij}={\sigma }_{ji}=\mathbb{E}[(x_i-{\mu }_i)(x_j-{\mu }_j)]$。因此，协方差矩阵$\Sigma$是 实对称矩阵。并且${\sigma }_{ii}=(x_i-{\mu }_i{)}^2\ge 0(i=1,2,\cdots ,p)$恒成立。因此$\Sigma$至少是半正定矩阵。
不排除${\sigma }_{ii}=0$的情况发生，因此这个协方差矩阵不一定是‘正定矩阵’。但在推导过程中暂时设定为‘正定矩阵’。

多维高斯分布的概率密度函数表示如下：
从‘概率模型’角度将高斯分布表示为$P(x\mid \mu ,\Sigma )$
$$x\sim \mathcal{N}(\mu ,\Sigma )=P(x\mid \mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{p}{2}}\cdot |\Sigma {|}^{\frac{1}{2}}}\exp \left\{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right\}$$
其中，$|\Sigma |$表示协方差矩阵的行列式结果；${\Sigma }^{-1}$表示协方差矩阵的逆矩阵。

观察：如果将$x$看作自变量/需要求解的量，$\mu ,\Sigma$看作多维高斯分布$\mathcal{N}(\mu ,\Sigma )$的参数，则整个概率密度函数公式中和$x$有关的部分只有：
$$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$$
首先观察它的维度：$(x-\mu )$是 $p\times 1$维向量，$(x-\mu {)}^T$自然是 $1\times p$维向量；协方差矩阵的逆不改变维度：${\Sigma }^{-1}\to p\times p$；因此，$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$本质上是一个一维矩阵，是个标量，是一个具体数值。

这里引进一个概念：马氏距离($\text{Mahalanobis distance}$)。它描述的是两个向量(高维空间内两个数据点)之间的距离描述。马氏距离传送门
例如$p$维空间的两个数据点：
$$\begin{gathered} x=(x_1,x_2,\cdots ,x_p{)}^T \\ y=(y_1,y_2,\cdots ,y_p{)}^T \end{gathered}$$
它们的马氏距离表示如下：
$${\mathcal{D}}_M(x,y)=\sqrt{(x-y{)}^T{\Sigma }^{-1}(x-y)}$$

在这里可以将$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$视作样本点$x$与样本均值向量$\mu$之间的马氏距离。

如果${\Sigma }^{-1}$是单位矩阵，马氏距离将退化为欧式距离($\text{Euclidean Distance}$)

假设协方差矩阵是正定矩阵，对协方差矩阵进行特征值分解：
如果协方差矩阵是一般情况下的‘半正定’，那么$\Sigma$自然是不能求逆的，${\Sigma }^{-1}$是不存在的。
$$\Sigma =U\Lambda U^T$$
根据特征值分解定义，$U$是一个正交矩阵，即：
$$U{U}^T=U^{T}U=I$$
其中$\mathcal{I}$表示单位矩阵，$U,I$矩阵格式均为$p\times p$。将正交矩阵$U$定义为$(u_1,u_2,\cdots ,u_p)$；其中$u_i(i=1,2,\cdots ,p)$看作$p\times 1$维向量。
$\Lambda$表示特征值向量，对角线上元素为$\Sigma$矩阵的特征值。
根据上式则有：
$$\begin{array}{rl}\Sigma & =U\Lambda U^T\\ & =(u_1,u_2,\cdots ,u_p)\left(\begin{array}{c}{\lambda }_0,0,\cdots ,0\\ 0,{\lambda }_1,\cdots ,0\\ ⋮\\ 0,0,\cdots ,{\lambda }_p\end{array}\right)\left(\begin{array}{c}{u}_1^T\\ u_2^T\\ ⋮\\ u_p^T\end{array}\right)\\ & =(u_1{\lambda }_1,u_2{\lambda }_2,\cdots ,u_p{\lambda }_p)\left(\begin{array}{c}{u}_1^T\\ u_2^T\\ ⋮\\ u_p^T\end{array}\right)\\ & =u_1{\lambda }_1{u}_1^T+u_2{\lambda }_2{u}_2^T+\cdots +u_p{\lambda }_p{u}_p^T\end{array}$$
由于${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_p$是特征值，是常数，因此可以提到前面，$u_i{u}_i^T$结果是$p\times p$的方阵；
$$\Sigma =\sum _{i=1}^p{\lambda }_i{u}_i{u}_i^T$$
基于上式，通过$\Sigma$求解${\Sigma }^{-1}$：
正交阵的性质，正交阵的转置等于该正交阵的逆。即：$U^T=U^{-1}$
$$\begin{array}{rl}{\Sigma }^{-1}& =(U\Lambda U^T{)}^{-1}\\ & =(U^T{)}^{-1}{\Lambda }^{-1}{U}^{-1}\\ & =U{\Lambda }^{-1}{U}^T\\ & =\sum _{i=1}^p\frac{1}{{\lambda }_i}{u}_i{u}_i^T\end{array}$$
将${\Sigma }^{-1}$带入$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$，则有：
$$\begin{array}{rl}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )& =(x-\mu {)}^T\left[\sum _{i=1}^p\frac{1}{{\lambda }_i}{u}_i{u}_i^T\right](x-\mu )\end{array}$$

观察，$(x-\mu {)}^T$是$1\times p$的向量；$\begin{array}{r}\sum _{i=1}^p\frac{1}{{\lambda }_i}{u}_i{u}_i^T\end{array}$是$p\times p$维向量；$(x-\mu )$是$p\times 1$维向量。
因此，$\begin{array}{r}(x-\mu {)}^T\left[\sum _{i=1}^p\frac{1}{{\lambda }_i}{u}_i{u}_i^T\right](x-\mu )\end{array}$仍然是一个标量、一个数值。
将$(x-\mu {)}^T,(x-\mu )$两个向量看成整体，不执行任何拆分，将$\begin{array}{r}\sum _{i=1}^p\frac{1}{{\lambda }_i}\end{array}$提出来：
$$\sum _{i=1}^p\frac{1}{{\lambda }_i}(x-\mu {)}^T\left[u_i{u}_i^T\right](x-\mu )$$
令向量$k={\left(\begin{array}{c}{k}_1\\ k_2\\ ⋮\\ k_p\end{array}\right)}_{p\times 1}$，$k_i(i=1,2,\cdots ,p)=(x-\mu {)}^T{u}_i$

上式可转化为：
$$\begin{array}{rl}\mathcal{I}& =\sum _{i=1}^p\frac{1}{{\lambda }_i}(x-\mu {)}^T{u}_i\cdot {\left[(x-\mu {)}^T{u}_i\right]}^T\\ & =\sum _{i=1}^p\frac{1}{{\lambda }_i}{k}_i{k}_i^T\end{array}$$

由于$k$的定义，因此，$k_i(i=1,2,\cdots ,p)$是标量、数值。即：
$$k_i^T=k_i$$
则有：
$$\begin{array}{rl}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )& =\sum _{i=1}^p\frac{1}{{\lambda }_i}{k}_i{k}_i^T\\ & =\sum _{i=1}^p\frac{k_i^2}{{\lambda }_i}(i=1,2,\cdots ,p)\end{array}$$

将上述结果展开：
$$\sum _{i=1}^p\frac{k_i^2}{{\lambda }_i}=\frac{k_1^2}{{\lambda }_1}+\frac{k_2^2}{{\lambda }_2}+\cdots +\frac{k_p^2}{{\lambda }_p}$$

如果给定上述结果一个具体的值：$\Delta$
则有：
$$\begin{array}{r}\frac{k_1^2}{{\lambda }_1}+\frac{k_2^2}{{\lambda }_2}+\cdots +\frac{k_p^2}{{\lambda }_p}=\Delta \\ \frac{1}{\Delta }(\frac{k_1^2}{{\lambda }_1}+\frac{k_2^2}{{\lambda }_2}+\cdots +\frac{k_p^2}{{\lambda }_p})=1\\ \frac{k_1^2}{\Delta {\lambda }_1}+\frac{k_2^2}{\Delta {\lambda }_2}+\cdots +\frac{k_p^2}{\Delta {\lambda }_p}=1\end{array}$$
它就是一个超椭圆形的标准方程。
令$p=2$：
$$\frac{k_1^2}{\Delta {\lambda }_1}+\frac{k_2^2}{\Delta {\lambda }_2}=1$$

它就是一个椭圆的标准方程，其中$a=\sqrt{\Delta {\lambda }_1},b=\sqrt{\Delta {\lambda }_2}$

至此，基于马氏距离$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$，它执行一次坐标系的映射：

• 原始$p$维坐标系$x_i(i=1,2,\cdots ,p)$;
• 经过一系列变换：$k_i=(x-\mu {)}^T{u}_i$
  将$x$坐标系先通过平移$\mu$个长度后，再映射到$u$坐标系中(矩阵乘法的特点)
• $k_i$表示在样本$x$在$u$坐标系中的映射结果。
• 而马氏距离$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$可理解为在$x$映射到$k$之后，构建一个椭圆，而椭圆上的值就是马氏距离的结果。
  
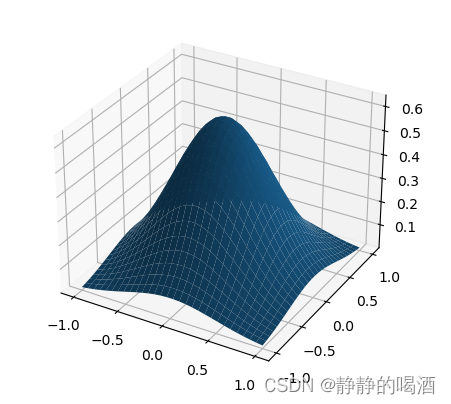
  上述表示$i=2$时的高斯分布图像，由于$x$只和$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$相关，和表示概率的$\begin{array}{r}\frac{1}{(2\pi {)}^{\frac{p}{2}}\cdot |\Sigma {|}^{\frac{1}{2}}}\end{array}$无关。

但是概率和$\Delta$相关，基于上述标准方程，椭圆的长轴和短轴长度分别是$\sqrt{\Delta {\lambda }_1},\sqrt{\Delta {\lambda }_2}$；选择的$\Delta$值直接影响椭圆的大小，从而影响获取横截面的位置。

因此，当概率被确定时，以上述图为例，在$z$轴对应概率值位置进行横切，而横切得到的横截面必然是椭圆形截面。而$(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )$表示椭圆形上的点。

高斯分布的局限性(2022/11/18)

回顾：协方差矩阵，马氏距离

回顾正常情况下(正定条件下) 协方差矩阵的表示：
$$\Sigma =\mathcal{U}\Lambda {\mathcal{U}}^T{\mathcal{U}}^T\mathcal{U}=\mathcal{U}{\mathcal{U}}^T=\mathcal{I}$$
其中$\mathcal{I}$是单位矩阵，由于协方差矩阵自身的性质，$\mathcal{U}$是各向量两两正交的正交矩阵：
$$\mathcal{U}=(u_1,u_2,\cdots ,u_p{)}_{p\times p}$$
某样本点$x$到对应分布的马氏距离$\Delta$表示如下：
需要补充的点：$k_i$并不是正交基，而是$x$坐标轴的元素$x-\mu$在$u$正交基上的投影坐标，是一个实数。
$$k_i=(x-\mu {)}^T\cdot u_i$$
$$\begin{array}{rl}\Delta & =(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\\ & =(x-\mu {)}^T\sum _{i=1}^p\frac{1}{{\lambda }_i}{u}_i{u}_i^T(x-\mu )\\ & =\sum _{i=1}^p\frac{1}{{\lambda }_i}\left[(x-\mu {)}^T\cdot u_i\right]\cdot {\left[(x-\mu {)}^T\cdot u_i\right]}^T\\ & =\sum _{i=1}^p\frac{1}{{\lambda }_i}{k}_i{k}_i^T\\ & =\sum _{i=1}^p\frac{k_i^2}{{\lambda }_i}(i=1,2,\cdots ,p)\end{array}$$
因此，马氏距离在正交基$\mathcal{U}=(u_1,u_2,\cdots ,u_p)$中的呈现的函数是一个标准椭圆形状。但是该椭圆仅在$\mathcal{U}$正交基下是标准的，但在$x$坐标轴中可能存在偏移：
这里图形均以二维坐标为例，下同。

局限性的具体体现

• 计算协方差矩阵参数的时间复杂度过高。
  协方差矩阵是一个$p\times p$的实对称矩阵，因此需要求解的元素包含上/下三角阵 + 对角阵的参数。具体参数数量$\delta$以及对应的时间复杂度为：
  $$\delta =\frac{p(p+1)}{2}\to O(p^2)$$
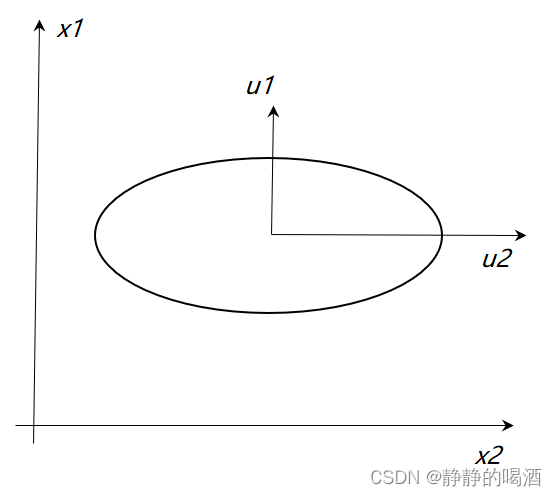
  为了减小时间复杂度，尝试对求解过程进行简化。
  • 假设协方差矩阵是对角矩阵。即：
    $$\Sigma =\mathcal{U}\Lambda {\mathcal{U}}^T\to \Lambda$$
    这意味着$\mathcal{U}$不仅仅是单纯的正交矩阵，并且是单位矩阵，矩阵内各向量均是两两相互正交的单位向量：
    $$\mathcal{U}={\mathcal{U}}^T=\mathcal{E}$$
    这使得正交基$u_i$和坐标轴$x_i$方向相同，此时仅需要计算 对角线上的$p$个特征值即可。
    $$\Delta =\sum _{i=1}^p\frac{1}{{\lambda }_i}{u}_i{u}_i^T$$
    协方差矩阵是对角阵对应在图中的表示如下：
    
  • 在上述假设的基础上，假设表示协方差矩阵$\Sigma$的对角阵中各元素均相同。即：
    $${\lambda }_1,={\lambda }_2=\cdots ={\lambda }_p=\lambda$$
    此时的马氏距离变化为：
    由于$\lambda$均相同，使得原始的超椭圆体的判别式变成一个超球体的判别式。
    $$\Delta =\frac{{\sum }_{i=1}^p{u}_i{u}_i^T}{\lambda }$$
    协方差矩阵是对角线元素相同的对角阵对应图像表示如下：
    
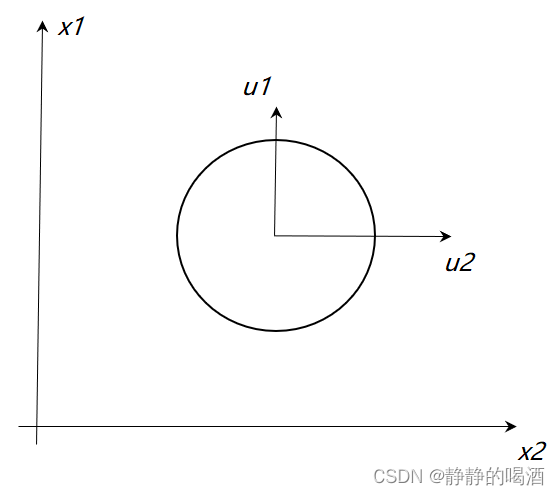
    此时的协方差矩阵仅需要计算一个特征值即可，大大简化了运算。将这种情况称为各向同性(isotropic)。具体的延伸方法有因子分析(Factor Analysis),概率性主成分分析(Probabilisitc PCA)等。
• 高斯分布自身的局限性——虽然高斯分布涉及范围很广泛，但是一些情况使用高斯分布建立概率模型 显得不足。最明显的如高斯混合模型的概率分布，其分布明显一个高斯分布无法进行表示。详见高斯混合模型——模型介绍。

总结

• 矩阵乘法——将当前变量的坐标系映射到其他坐标系中；
  在后续的线性判别分析中加深印象;
• 将$x$参考系被映射到新的参考系中，并将马氏距离映射为标准的超椭圆方程。

相关参考：
机器学习-数学基础-概率-高斯分布3-从概率密度角度观察
机器学习-数学基础-概率-高斯分布4-局限性