机器学习笔记之概率图模型——贝叶斯网络的结构表示
引言
上一节介绍了概率图模型的背景以及相关任务。本节将从有向图(贝叶斯网络)出发,介绍贝叶斯网络的结构表示(Representation)。
回顾:
概率图的本质
概率图模型这个概念想要表达的核心是:变量之间的相关性信息。实际上,在朴素贝叶斯分类器一节中,就已经对这个相关性信息进行了初步探索。
在介绍朴素贝叶斯假设与高斯判别分析之间的区别时,两者之间的主要区别在于:相比于高斯判别分析对整个数据集合的概率分布 P ( X ∣ Y ) \mathcal P(\mathcal X \mid \mathcal Y) P(X∣Y)进行假设,朴素贝叶斯分类器对 P ( X ∣ Y ) \mathcal P(\mathcal X \mid \mathcal Y) P(X∣Y)的假设更加细致,它的想法精确到了样本 X \mathcal X X的各个维度。
-
以二分类为例,高斯判别分析的假设表示如下:
Y ∼ B e r n o u l l i ( ϕ ) X ∣ Y = 0 ∼ N ( μ 1 , Σ ) X ∣ Y = 1 ∼ N ( μ 2 , Σ ) \mathcal Y \sim Bernoulli(\phi) \\ \mathcal X \mid \mathcal Y = 0 \sim \mathcal N(\mu_1,\Sigma) \\ \mathcal X \mid \mathcal Y = 1 \sim \mathcal N(\mu_2,\Sigma) Y∼Bernoulli(ϕ)X∣Y=0∼N(μ1,Σ)X∣Y=1∼N(μ2,Σ)这里关注的重点在于:无论样本集合 X \mathcal X X的维度是多少,在标签 Y \mathcal Y Y确定的条件下, X \mathcal X X的每个维度均服从相同的概率分布。
-
依然以二分类为例,朴素贝叶斯的假设表示如下:
x i ⊥ x j ∣ Y ( i , j ∈ { 1 , 2 , ⋯ , p } ; i ≠ j ; Y ∈ { 0 , 1 } ) P ( X ∣ Y ) = P ( x 1 , ⋯ , x p ∣ Y ) = ∏ i = 1 p P ( x i ∣ Y ) x_i \perp x_j \mid \mathcal Y \quad (i,j \in \{1,2,\cdots,p\};i\neq j;\mathcal Y \in \{0,1\}) \\ \begin{aligned} \mathcal P(\mathcal X \mid \mathcal Y) & = \mathcal P(x_1,\cdots,x_p \mid \mathcal Y) \\ & = \prod_{i=1}^p \mathcal P(x_i \mid \mathcal Y) \end{aligned} xi⊥xj∣Y(i,j∈{1,2,⋯,p};i=j;Y∈{0,1})P(X∣Y)=P(x1,⋯,xp∣Y)=i=1∏pP(xi∣Y)
虽然这个假设非常简单,以至于假设的条件非常苛刻,但是该模型确实对样本集合的维度进行了更加细致的假设。
而概率图模型相比于朴素贝叶斯假设以及马尔可夫性质,它对变量/特征们的约束更加宽松,基于条件独立性假设,将变量/特征们之间的关联关系表示为图结构:
- 若变量/特征们之间存在显示的因果关系(在概率图中结点之间可用箭头连接),则使用 贝叶斯网络构建概率图;
- 若变量/特征们之间仅知道存在相关性(在概率图中即结点之间存在边,但箭头方向未知),则使用 马尔可夫网络/马尔可夫随机场构建概率图。
条件独立性与链式法则
针对样本集合
X
\mathcal X
X的 概率分布/概率模型
P
(
X
)
\mathcal P(\mathcal X)
P(X),我们从维度角度观察,可将
P
(
X
)
\mathcal P(\mathcal X)
P(X)看作成各维度信息的联合概率分布形式:
P
(
X
)
=
P
(
x
1
,
x
2
,
⋯
,
x
p
)
\mathcal P(\mathcal X) = \mathcal P(x_1,x_2,\cdots,x_p)
P(X)=P(x1,x2,⋯,xp)
针对联合概率分布的求解,最朴素的方法是条件概率的链式法则:
P
(
x
1
,
x
2
,
x
3
)
=
P
(
x
1
)
⋅
P
(
x
2
∣
x
1
)
⋅
P
(
x
3
∣
x
1
,
x
2
)
P
(
x
1
,
⋯
,
x
p
)
=
P
(
x
1
)
⋅
∏
i
=
2
p
P
(
x
i
∣
x
1
,
⋯
,
x
i
−
1
)
\begin{aligned} \mathcal P(x_1,x_2,x_3) & = \mathcal P(x_1) \cdot \mathcal P(x_2 \mid x_1) \cdot \mathcal P(x_3 \mid x_1,x_2) \\ \mathcal P(x_1,\cdots,x_p) & = \mathcal P(x_1) \cdot \prod_{i=2}^p \mathcal P(x_i \mid x_1,\cdots,x_{i-1}) \end{aligned}
P(x1,x2,x3)P(x1,⋯,xp)=P(x1)⋅P(x2∣x1)⋅P(x3∣x1,x2)=P(x1)⋅i=2∏pP(xi∣x1,⋯,xi−1)
由于 X \mathcal X X维度过高的情况下,链式法则求解 P ( x 1 , ⋯ , x p ) \mathcal P(x_1,\cdots,x_p) P(x1,⋯,xp)的计算量极高,因为链式法则中,任意两个特征/变量我们都要求解其关联关系。
而条件独立性在 最小化约束特征之间关系的同时,还可以极大程度地简化运算:
x
A
⊥
x
B
∣
x
C
x_{\mathcal A} \perp x_{\mathcal B} \mid x_{\mathcal C}
xA⊥xB∣xC
其中
x
A
,
x
B
,
x
C
x_{\mathcal A},x_{\mathcal B},x_{\mathcal C}
xA,xB,xC表示一个或者多个变量/特征组成的集合,并且
x
A
,
x
B
,
x
C
x_{\mathcal A},x_{\mathcal B},x_{\mathcal C}
xA,xB,xC内元素互不相交。
而条件独立性的文字描述 即:在
x
C
x_{\mathcal C}
xC中变量给定的条件下,
x
A
,
x
B
x_{\mathcal A},x_{\mathcal B}
xA,xB变量之间相互独立。
贝叶斯网络与条件独立性
条件概率对边的方向性表达
贝叶斯网络根据条件独立性,通过有向图 对联合概率分布进行表达。
一个贝叶斯网络由结构表示
G
\mathcal G
G和参数集合
Θ
\Theta
Θ两部分构成,而
G
\mathcal G
G是一个 有向无环图,每个结点对应一个随机变量/特征;两个结点之间连接的边表示两结点之间存在显式的因果关系,从而使用
Θ
\Theta
Θ集合中两结点的对应结果表示这种关系。
注意关于结点的描述:无论是视频还是西瓜书,都对结点的描述是‘一个属性/特征’,而不是特征集合的形式。欢迎小伙伴一起讨论。
示例1:以两个结点的贝叶斯网络为例:
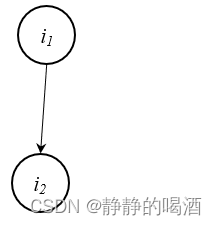
观察上述有向图,我们使用条件概率对该有向边的方向性进行表示。具体表示如下:
由于整个‘贝叶斯网络’只有一条有向边,因此‘参数集合’
Θ
\Theta
Θ表示该有向边的条件概率信息。
P
(
i
2
∣
i
1
)
=
Θ
\mathcal P(i_2 \mid i_1) = \Theta
P(i2∣i1)=Θ
假设特征
i
1
,
i
2
i_1,i_2
i1,i2均服从伯努利分布,参数集合
Θ
\Theta
Θ示例如下:
明显是一个‘右随机矩阵’~
| i 1 = 0 i_1 = 0 i1=0 | i 1 = 1 i_1 = 1 i1=1 | |
|---|---|---|
| i 2 = 0 i_2 = 0 i2=0 | 0.1 0.1 0.1 | 0.9 0.9 0.9 |
| i 2 = 1 i_2 = 1 i2=1 | 0.7 0.7 0.7 | 0.3 0.3 0.3 |
因此,上述概率图中有向边的方向性可以进行如下表达:
P
(
i
2
=
0
∣
i
1
=
1
)
=
0.9
\mathcal P(i_2 = 0 \mid i_1 = 1) = 0.9
P(i2=0∣i1=1)=0.9
基于贝叶斯网络列出联合概率分布
如何表示上述贝叶斯网络的联合概率分布,即 P ( i 1 , i 2 ) \mathcal P(i_1,i_2) P(i1,i2)?
- 首先找到入度为零的结点,并指定该特征的概率为边缘概率。在当前概率图中,入度为零的结点时
i
1
i_1
i1,它的概率结果表示为:
P
(
i
1
)
\mathcal P(i_1)
P(i1)。
由于‘入度为零’的结点的概率不需要其他结点作为条件而发生,因此时边缘概率。 - 找出图中的有向边,并对有向边的方向性进行表达:
P ( i 2 ∣ i 1 ) \mathcal P(i_2 \mid i_1) P(i2∣i1) - 此时,图中全部结点和有向边全部表示完成,联合概率分布表示如下:
P ( i 1 , i 2 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) \mathcal P(i_1,i_2) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) P(i1,i2)=P(i1)⋅P(i2∣i1)
示例2:构造一个稍复杂的贝叶斯网络如下:
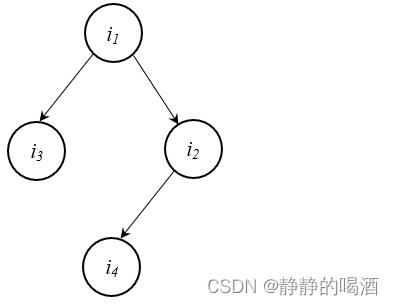
根据上述步骤,联合概率分布表示如下:
- 找出入度为零结点 i 1 → P ( i 1 ) i_1 \to \mathcal P(i_1) i1→P(i1);
- 图中一共包含
3
3
3条有向边,对应条件概率表示如下:
P ( i 2 ∣ i 1 ) , P ( i 3 ∣ i 1 ) , P ( i 4 ∣ i 2 ) \mathcal P(i_2 \mid i_1),\mathcal P(i_3 \mid i_1),\mathcal P(i_4 \mid i_2) P(i2∣i1),P(i3∣i1),P(i4∣i2) - 最终联合概率分布
P
(
i
1
,
i
2
,
i
3
,
i
4
)
\mathcal P(i_1,i_2,i_3,i_4)
P(i1,i2,i3,i4)表示如下:
P ( i 1 , i 2 , i 3 , i 4 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 ) ⋅ P ( i 4 ∣ i 2 ) \mathcal P(i_1,i_2,i_3,i_4) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1)\cdot \mathcal P(i_3 \mid i_1)\cdot \mathcal P(i_4 \mid i_2) P(i1,i2,i3,i4)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1)⋅P(i4∣i2)
基于联合概率分布构建概率图
如何基于给定的联合概率分布构建概率图?
使用拓扑排序的顺序进行构建。
示例3:已知联合概率分布表示如下:
P
(
i
1
,
i
2
,
i
3
,
i
4
,
i
5
)
=
P
(
i
1
)
⋅
P
(
i
2
)
⋅
P
(
i
3
∣
i
1
)
⋅
P
(
i
4
∣
i
1
,
i
2
)
⋅
P
(
i
5
∣
i
2
)
\mathcal P(i_1,i_2,i_3,i_4,i_5) = \mathcal P(i_1) \cdot \mathcal P(i_2) \cdot \mathcal P(i_3 \mid i_1) \cdot \mathcal P(i_4 \mid i_1,i_2) \cdot \mathcal P(i_5 \mid i_2)
P(i1,i2,i3,i4,i5)=P(i1)⋅P(i2)⋅P(i3∣i1)⋅P(i4∣i1,i2)⋅P(i5∣i2)
- 首先,找到入度为零的结点,即拓扑排序的初始结点,在联合概率分布中,该结点即 写成边缘概率分布形式的结点,这里是指
i
1
,
i
2
i_1,i_2
i1,i2,并将该结点存储起来:

- 基于该结点,分别找到以入度为零结点或者其联合概率分布作为条件的条件概率:这里是指
P
(
i
3
∣
i
1
)
,
P
(
i
5
∣
i
2
)
P
(
i
4
∣
i
1
,
i
2
)
\mathcal P(i_3 \mid i_1),\mathcal P(i_5 \mid i_2)\mathcal P(i_4 \mid i_1,i_2)
P(i3∣i1),P(i5∣i2)P(i4∣i1,i2)。并将探索到的结点
i
3
,
i
5
,
i
4
i_3,i_5,i_4
i3,i5,i4存储起来;
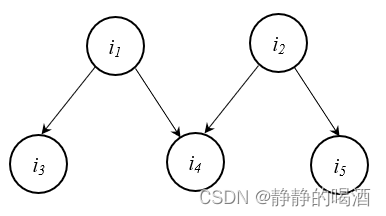
- 观察联合概率分布中的各项是否表示完成,若未完成,查找以存储结点或者其联合概率分布为条件,查找满足条件的项,从而找出新的结点。如果完成,则结束查找。
基于上述逻辑,如果给定贝叶斯网络的表达方式,我们可以根据贝叶斯网络写出各结点的联合概率分布:
称其为’因子分解‘。
P
(
x
1
,
x
2
,
⋯
,
x
p
)
=
∏
i
=
1
p
P
(
x
i
∣
x
p
a
(
i
)
)
\mathcal P(x_1,x_2,\cdots,x_p) = \prod_{i=1}^p \mathcal P(x_i \mid x_{pa(i)})
P(x1,x2,⋯,xp)=i=1∏pP(xi∣xpa(i))
其中
x
p
a
(
i
)
x_{pa(i)}
xpa(i)表示结点
x
i
x_i
xi的父结点组成的集合。所谓父结点,即通过有向边指向结点
x
i
x_i
xi的结点。可以看出,父结点可能不唯一,如上图中的
i
4
i_4
i4结点,其父结点包含两个:
i
1
,
i
2
i_1,i_2
i1,i2。
对比原始联合概率分布表达和基于概率图产生的联合概率分布:
{
P
(
x
1
,
⋯
,
x
p
)
=
P
(
x
1
)
⋅
∏
i
=
2
p
P
(
x
i
∣
x
1
,
⋯
,
x
i
−
1
)
P
(
x
1
,
x
2
,
⋯
,
x
p
)
=
∏
i
=
1
p
P
(
x
i
∣
x
p
a
(
i
)
)
\begin{cases} \mathcal P(x_1,\cdots,x_p) = \mathcal P(x_1) \cdot \prod_{i=2}^p \mathcal P(x_i \mid x_1,\cdots,x_{i-1}) \\ \mathcal P(x_1,x_2,\cdots,x_p) = \prod_{i=1}^p \mathcal P(x_i \mid x_{pa(i)}) \end{cases}
{P(x1,⋯,xp)=P(x1)⋅∏i=2pP(xi∣x1,⋯,xi−1)P(x1,x2,⋯,xp)=∏i=1pP(xi∣xpa(i))
明显可以看出基于概率图产生的联合概率分布,它的条件项部分明显减少了:
将原始条件中的
i
−
1
i-1
i−1个结点减少为若干个存在关联关系的’父结点‘。这种操作极大程度地简化了运算。
x
1
,
x
2
,
⋯
,
x
i
−
1
→
x
p
a
(
i
)
x_1,x_2,\cdots,x_{i-1} \to x_{pa(i)}
x1,x2,⋯,xi−1→xpa(i)
关于概率图的逻辑:
之所以可以使用 因子分解 的方式表达联合概率分布,是基于概率图能够表达概率模型
P
(
X
)
\mathcal P(\mathcal X)
P(X)中的条件独立性。如果概率图不能表达特征中的条件独立性,概率图自身无意义。
相反,并不是所有的概率模型都可以使用概率图进行表达,如果样本集合 X \mathcal X X的概率模型 P ( X ) \mathcal P(\mathcal X) P(X)自身没有条件独立性,概率图自然也无法构建出来。
概率图中条件独立性的识别
同父结构
假设已知存在一个概率图,该概率图内部存在如下形状:
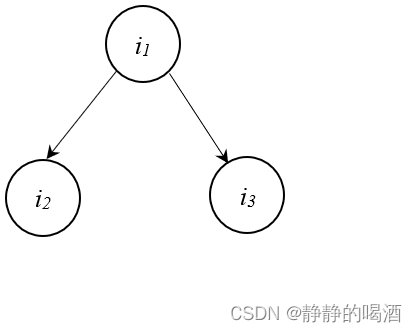
我们称该结构为同父结构(Common Parent),即结点 i 2 , i 3 i_2,i_3 i2,i3存在相同的父结点 i 1 i_1 i1。该结构中表现出的现象是:给定父结点 i 1 i_1 i1的取值,则 i 2 , i 3 i_2,i_3 i2,i3条件独立。具体推导如下:
- 首先通过因子分解描述该形状的联合概率分布
P
(
i
1
,
i
2
,
i
3
)
\mathcal P(i_1,i_2,i_3)
P(i1,i2,i3):
P ( i 1 , i 2 , i 3 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 ) \mathcal P(i_1,i_2,i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1) P(i1,i2,i3)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1) - 再通过联合概率分布的链式法则求解联合概率分布
P
(
i
1
,
i
2
,
i
3
)
\mathcal P(i_1,i_2,i_3)
P(i1,i2,i3):
链式法则就和’概率图‘没有什么关系了,它是一直成立的。
P ( i 1 , i 2 , i 3 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_1,i_2,i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) P(i1,i2,i3)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2) - 这两个公式描述的是同一个概率分布,则有:
P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) P(i1)⋅P(i2∣i1)⋅P(i3∣i1)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2)
消去 P ( i 1 ) , P ( i 2 ∣ i 1 ) \mathcal P(i_1),\mathcal P(i_2 \mid i_1) P(i1),P(i2∣i1),有:
但从该式观察,i 2 i_2 i2无论是否作为条件发生,都不会影响i 3 i_3 i3的条件概率结果,这实际上已经证明了i 2 , i 3 i_2,i_3 i2,i3相互独立。
P ( i 3 ∣ i 1 , i 2 ) = P ( i 3 ∣ i 1 ) \mathcal P(i_3 \mid i_1,i_2) = \mathcal P(i_3 \mid i_1) P(i3∣i1,i2)=P(i3∣i1) - 基于上述等式,最优两端同乘
P
(
i
2
∣
i
1
)
\mathcal P(i_2 \mid i_1)
P(i2∣i1):
P ( i 3 ∣ i 1 , i 2 ) ⋅ P ( i 2 ∣ i 1 ) = P ( i 3 ∣ i 1 ) ⋅ P ( i 2 ∣ i 1 ) P ( i 2 , i 3 ∣ i 1 ) = P ( i 3 ∣ i 1 ) ⋅ P ( i 2 ∣ i 1 ) \mathcal P(i_3 \mid i_1,i_2) \cdot \mathcal P(i_2 \mid i_1) = \mathcal P(i_3 \mid i_1) \cdot \mathcal P(i_2 \mid i_1) \\ \mathcal P(i_2,i_3 \mid i_1) = \mathcal P(i_3 \mid i_1) \cdot \mathcal P(i_2 \mid i_1) P(i3∣i1,i2)⋅P(i2∣i1)=P(i3∣i1)⋅P(i2∣i1)P(i2,i3∣i1)=P(i3∣i1)⋅P(i2∣i1)
该公式意味着:结点 i 1 i_1 i1给定的条件下, i 2 , i 3 i_2,i_3 i2,i3的联合概率分布结果等于各自条件概率的乘积结果。即 给定 i 1 i_1 i1条件下, i 2 , i 3 i_2,i_3 i2,i3相互独立:
i 2 ⊥ i 3 ∣ i 1 i_2 \perp i_3 \mid i_1 i2⊥i3∣i1
如果从概率图本身角度出发,同父结构 本身就蕴含了条件独立性。而并非是将条件独立性强加给同父结构产生的结果。后续结构同理。
顺序结构
假设概率图中存在如下形状:
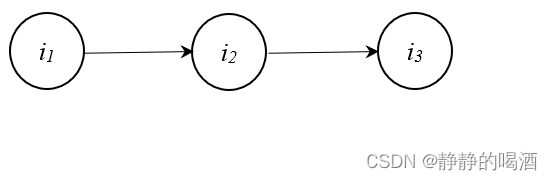
我们称该结构为顺序结构,即
i
1
,
i
2
,
i
3
i_1,i_2,i_3
i1,i2,i3三个结点首位相连。该结构表现的现象是:当
i
2
i_2
i2被观测时,
i
1
,
i
3
i_1,i_3
i1,i3相互独立。具体推导过程如下:
- 通过因子分解描述顺序结构情况下的联合概率分布:
将‘同父结构’与‘顺序结构’的联合概率分布进行对比,只是最后一项存在差异,但推导过程与‘同父结构’中完全相同。
{ P ( i 1 , i 2 , i 3 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 ) C o m m o n P a r e n t P ( i 1 , i 2 , i 3 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) S e q u e n c e \begin{cases} \mathcal P(i_1,i_2,i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1) \quad Common Parent \\ \mathcal P(i_1,i_2,i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \quad Sequence \end{cases} {P(i1,i2,i3)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1)CommonParentP(i1,i2,i3)=P(i1)⋅P(i2∣i1)⋅P(i3∣i2)Sequence - 对应的链式法则表示结果:
P ( i 1 , i 2 , i 3 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_1,i_2,i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) P(i1,i2,i3)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2) - 两联合概率取等,有:
P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 2 ) P ( i 3 ∣ i 1 , i 2 ) = P ( i 3 ∣ i 2 ) \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \\ \mathcal P(i_3 \mid i_1,i_2) = \mathcal P(i_3 \mid i_2) P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2)=P(i1)⋅P(i2∣i1)⋅P(i3∣i2)P(i3∣i1,i2)=P(i3∣i2) - 等式两边同乘
P
(
i
1
∣
i
2
)
\mathcal P(i_1 \mid i_2)
P(i1∣i2):
P ( i 1 ∣ i 2 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) = P ( i 3 ∣ i 2 ) ⋅ P ( i 1 ∣ i 2 ) P ( i 1 , i 3 ∣ i 2 ) = P ( i 3 ∣ i 2 ) ⋅ P ( i 1 ∣ i 2 ) \mathcal P(i_1 \mid i_2) \cdot \mathcal P(i_3 \mid i_1,i_2) = \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_1 \mid i_2) \\ \mathcal P(i_1,i_3 \mid i_2) = \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_1 \mid i_2) P(i1∣i2)⋅P(i3∣i1,i2)=P(i3∣i2)⋅P(i1∣i2)P(i1,i3∣i2)=P(i3∣i2)⋅P(i1∣i2)
该公式意味着:结点 i 2 i_2 i2给定的条件下, i 1 , i 3 i_1,i_3 i1,i3的联合概率分布结果等于各自条件概率的乘积结果。即 给定 i 2 i_2 i2条件下, i 1 , i 3 i_1,i_3 i1,i3相互独立:
i 1 ⊥ i 3 ∣ i 2 i_1 \perp i_3 \mid i_2 i1⊥i3∣i2
V \mathcal V V型结构
V
\mathcal V
V型结构(V-structure)也称冲撞结构,其对应形状表示如下:
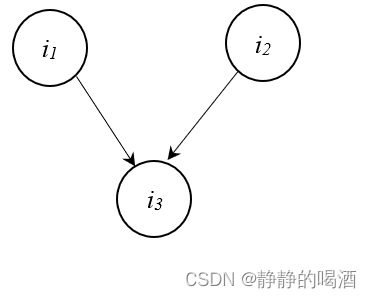
该结构表现的现象是:结点
i
3
i_3
i3给定的条件下,
i
1
,
i
2
i_1,i_2
i1,i2必不独立;若
i
3
i_3
i3结点取值未知,
i
1
,
i
2
i_1,i_2
i1,i2相互独立。
对该现象进行解释:
针对该现象的个人理解,只能解释后半部分,而前半部分是后半部分对立条件下产生的结果。
首先解释什么是给定,什么是未知?
回顾条件概率的定义式:
P
(
A
∣
B
)
\mathcal P(\mathcal A \mid \mathcal B)
P(A∣B)
上式是指事件
A
\mathcal A
A在另外一个事件
B
\mathcal B
B已经发生条件下的发生概率。这句话中,我们能够得到两个信息:
- 事件 B \mathcal B B是 已经发生的,是给定的;
- 事件 A \mathcal A A发生是以概率的形式表现的。因此,事件 A \mathcal A A是否发生是未知的。
回顾顺序结构和同父结构,它们的描述与对应的概率结果是同步的:
- 顺序结构:给定
i
2
i_2
i2条件下,则
i
1
,
i
3
i_1,i_3
i1,i3相互独立:
i 2 i_2 i2在‘|’后面,它是给定的。
P ( i 1 , i 3 ∣ i 2 ) = P ( i 3 ∣ i 2 ) ⋅ P ( i 1 ∣ i 2 ) \mathcal P(i_1,i_3 \mid i_2) = \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_1 \mid i_2) P(i1,i3∣i2)=P(i3∣i2)⋅P(i1∣i2) - 同父结构:给定
i
1
i_1
i1条件下,则
i
2
,
i
3
i_2,i_3
i2,i3条件独立:
i 1 i_1 i1在'|'后面,它是给定的。
P ( i 2 , i 3 ∣ i 1 ) = P ( i 3 ∣ i 1 ) ⋅ P ( i 2 ∣ i 1 ) \mathcal P(i_2,i_3 \mid i_1) = \mathcal P(i_3 \mid i_1) \cdot \mathcal P(i_2 \mid i_1) P(i2,i3∣i1)=P(i3∣i1)⋅P(i2∣i1)
根据上面的规律,有:
在条件概率的条件部分('|'后面),就是给定的;在条件概率的概率部分(‘|’前面),就是未知的。
至此,我们针对 V \mathcal V V型结构的推导如下:
- 通过因子分解描述
V
\mathcal V
V型结构情况下的联合概率分布:
P ( i 1 , i 2 , i 3 ) = P ( i 1 ) ⋅ P ( i 2 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_1,i_2,i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2) \cdot \mathcal P(i_3 \mid i_1,i_2) P(i1,i2,i3)=P(i1)⋅P(i2)⋅P(i3∣i1,i2) - 通过链式法则求解
V
\mathcal V
V型结构情况下的联合概率分布:
P ( i 1 , i 2 , i 3 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_1,i_2,i_3) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) P(i1,i2,i3)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2) - 上述两个联合概率分布取等。有:
P ( i 1 ) ⋅ P ( i 2 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) = P ( i 1 ) ⋅ P ( i 2 ∣ i 1 ) ⋅ P ( i 3 ∣ i 1 , i 2 ) P ( i 2 ) = P ( i 2 ∣ i 1 ) \mathcal P(i_1) \cdot \mathcal P(i_2) \cdot \mathcal P(i_3 \mid i_1,i_2) = \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_1,i_2) \\ \mathcal P(i_2) = \mathcal P(i_2 \mid i_1) P(i1)⋅P(i2)⋅P(i3∣i1,i2)=P(i1)⋅P(i2∣i1)⋅P(i3∣i1,i2)P(i2)=P(i2∣i1)
观察上述等式,
i
1
i_1
i1是否作为条件对
i
2
i_2
i2的概率均不产生影响,即
i
1
,
i
2
i_1,i_2
i1,i2相互独立。
但是此时的相互独立是建立在
i
3
i_3
i3给定还是未知的条件下成立的?
回头观察 i 3 i_3 i3在条件概率 P ( i 3 ∣ i 1 , i 2 ) \mathcal P(i_3 \mid i_1,i_2) P(i3∣i1,i2)的位置:在‘|’前面,说明 i 3 i_3 i3是未知的。因此有了结论的后半部分:若 i 3 i_3 i3结点取值未知, i 1 , i 2 i_1,i_2 i1,i2相互独立。
下一节将介绍贝叶斯网络结构表示中的有向分离,即 D \mathcal D D划分。
相关参考:
机器学习-周志华著
条件概率-百度百科
机器学习-概率图模型2-贝叶斯网络-Representation-条件独立性























 1048
1048











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










