非线性规划(NP)
定义:求一个函数min或max问题中,目标函数或约束条件至少有一个是非线性函数。
一般形式:
目标函数:
约束条件:
其中,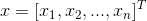
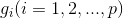
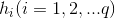
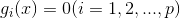
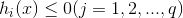
- Matlab标准形式
其中,f(x)是标量函数;A,B,Aeq,Beq是相应维数的矩阵和向量;C(x),Ceq(x)是非线性向量函数。
Matlab命令为
x=fmincon(fun,X0,A,B,Aeq,Beq,LB,UB,NONLCON,OPTIONS)
其返回值为向量 x 。其中,fun为需额外用M文件定义的目标函数;X0为x的初始值;A,B,Aeq,Beq对应线性不等约束








 本文介绍了Matlab在数学建模中的应用,主要聚焦于非线性规划(NP)和整数规划。非线性规划涉及目标函数和约束条件至少一个非线性的优化问题,Matlab通过fmincon函数进行求解。整数规划则是限制变量为整数的优化问题,包括分支定界法、割平面法、隐枚举法和匈牙利法等多种求解策略。
本文介绍了Matlab在数学建模中的应用,主要聚焦于非线性规划(NP)和整数规划。非线性规划涉及目标函数和约束条件至少一个非线性的优化问题,Matlab通过fmincon函数进行求解。整数规划则是限制变量为整数的优化问题,包括分支定界法、割平面法、隐枚举法和匈牙利法等多种求解策略。
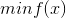
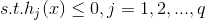
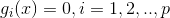
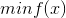
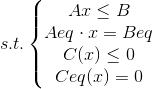
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1088
1088

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








