旋转卡壳——对踵点对（定义)

出自：http://blog.csdn.net/acmaker/article/details/3561145

对踵点对

切线

给定一个凸多边形  P ， 切线  l  是一条与  P  相交并且  P  的内部在  l  的一侧的线。 

这个概念与正交切线相似。 

对踵点对

如果两个点  p  和  q  （属于  P ） 在两条平行切线上， 那么他们就形成了一个对踵点对。 

两条不同的平行切线总是确定了至少一对的对踵点对。 根据线与多边形的相交方式， 呈现出三种情况：

1. “点-点”对踵点对
2. “点-边”对踵点对
3. “边-边”对踵点对

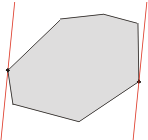情况1如图所示， 发生在切线对与多边形只有两个交点的时候。 途中的黑点构成了一个对踵点对。 

情况2如图所示，发生在其中一条切线与多边形交集为其一条边， 并且另一条切线与多边形的切点唯一的时候 。 此处注意这种切线的存在必然包含两个不同“点-点”对踵点对的存在。 

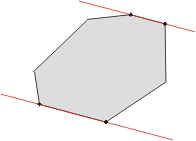情况3发生在切线与多边形交于平行边的时候。 这种情况下， 切线同样确定了四个不同的“点-点”对踵点对。