R语言--数据挖掘6--探索性分类建模分析

探索性分类建模分析

本报告的主要内容：

1. 对报告使用的iris数据和wine数据做介绍。
2. 简要介绍基本判别分析、朴素贝叶斯和k近邻的原理。
3. 结合原理进行建模分析。
4. 对本次报告的总结。
5. 代码以及参考。

数据介绍

本次报告主要使用两个数据：鸢尾花iris数据和酒wine的数据。

鸢尾花iris数据：主要有5个字段变量，150个观测数据。其中前4个变量分别是Speal.Length, Sepal.Width, Petal.Length, Petal.Width，它们是我们主要用这4个变量来进行分析，最后一个变量Species是花的类别。在本例中若用于聚类，可以用其作为最后分类结果的检测；若用于分类，可以作为有监督学习方法中的标签来训练数据，获得模型，并用于预测新数据的类型。

酒wine数据：主要有14个变量，178个观测数据。其中第一个变量是酒的品种cultivars，后面Alcohol, Malic acid, Ash, Alcalinity of ash, Magnesium等13个变量辨识这些葡萄酒的品种的主要成分变量。这些酒一共有三类，他们分别是从酒的化学分析中得到的，这些酒是生成在意大利的同一个地区中，但是却来源于三个品种。

基本原理介绍

判别分析

**简介：**判别分析是一个基于贝叶斯定理对观测数据进行分类的传统的分类方法。它适用于连续型自变量、名义型因变量的情形。

**假设：**我们的因变量$Y$有$K$类，对$l=1,\cdots ,K$，令${\xi }_l$表示类别$l$的先验概率。他们满足概率的完备性：${\sum }_{l=0}^K{\xi }_l=1$，设对属于类别$Y=l$的观测，自变量$X=(X_1,\cdots ,X_n)$的概率函数或概率密度函数为$f_l(x)$. 根据贝叶斯公式:
$$Pr(Y=l|\mathbf{X}=\mathbf{x})=\frac{Pr(Y=l)f(\mathbf{x}|Y=l)}{{\sum }_{l^{\prime }=1}^{K}Pr(Y=l^{\prime })f(\mathbf{x}|Y=l^{\prime })}=\frac{{\xi }_l{f}_l(\mathbf{x})}{{\sum }_{l^{\prime }=1}^K{\xi }_{l^{\prime }}{f}_{l^{\prime }}(\mathbf{x})}$$
**分类准则：**对于自变量为$\mathbf{x}$的观测，如果$Pr(Y=l^{\ast }|\mathbf{X}=\mathbf{x})$达到最大（因为分母等于事件$Pr(\mathbf{X}=\mathbf{x})$的概率，与$Y=l$发生的概率无关，所以它等价于使得${\xi }_l{f}_l(\mathbf{x})$最大），这时将其归为$Y=l^{\ast }$类。

接下来开始介绍两种常见的判别分析方法：线性判别分析和二次判别分析。

在进行介绍线性判别分析之间，首先先简要介绍一下为什么判别分析分为两个，一个是线性一个是非线性二次的。其实这主要是基于最开始作出的假设不同（各个类的方差是否相等），参数估计的不同引起的差异。因为这是传统的统计分析方法，而这些方法也是基于一些假设的，判别分析就是这其中一种。

线性判别分析方法描述：

首先作出假设：

1. 假设所有类的总体的方差相等，即${\Sigma }_1={\Sigma }_2=\cdots ={\Sigma }_K=\Sigma$

2. 可以推出：
   l o g ( ξ l f l ( x ) ) = l o g [ ξ l 1 ( 2 π ) p / 2 ∣ Σ ∣ 1 / 2 e x p { − 1 2 ( x − μ l ) T Σ − 1 ( x − μ l ) } ] = δ l ( x ) + A \begin{aligned} \mathbb{log}(\xi_l f_l(\boldsymbol{x})) &= \mathbb{log}\left[ \xi_l \cfrac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}} \mathbb{exp}\{- \cfrac{1}{2}(\boldsymbol{x} - \boldsymbol{\mu_l})^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu_l})\}\right] \\ &= \delta_l(\boldsymbol{x}) + A \end{aligned} log(ξl​fl​(x))​=log[ξl​(2π)p/2∣Σ∣1/21​exp{−21​(x−μl​)TΣ−1(x−μl​)}]=δl​(x)+A​
   其中
   $$\begin{array}{rl}& {\delta }_l(\mathbf{x})=log({\xi }_l)-\frac{1}{2}{\mathbf{x}}^T{\Sigma }^{-1}\mathbf{x}+{\mathbf{\mu }}_l^T{\Sigma }^{-1}\mathbf{x}\\ & A=\frac{p}{2}log(2\pi )-\frac{1}{2}log(|\Sigma |)-\frac{1}{2}{\mathbf{x}}^T{\Sigma }^{-1}\mathbf{x}\end{array}$$
   其中$A$虽然与$\mathbf{x}$有关，但是与我们所想分的类别无关，在这里我们只关注与类别$l$有关的变量，它是上式的${\delta }_l(\mathbf{x})$，又因为${\delta }_l(\mathbf{x})$中$\mathbf{x}$的系数只有一次，所以这是线性判别分析。

   判别准则：将使得$log({\xi }_l{f}_l(\mathbf{x}))$最大的类别$l$作为我们最后判别得到的类别。

3. 类别$l$和$l^{\prime }$之间的边界由${\delta }_l(\mathbf{x})={\delta }_{l^{\prime }}(\mathbf{x})$给出，该边界对于$\mathbf{x}$是线性的。

二次判别分析方法的描述：

步骤：

1. 首先也是作出假设：所有类的总体的方差不等。

2. 可以推出${\xi }_l{f}_l(\mathbf{x})$等价于
   $${\psi }_l(\mathbf{x})=log({\xi }_l)-\frac{1}{2}log(|{\Sigma }_l|)-\frac{1}{2}(\mathbf{x}-{\mathbf{\mu }}_l{)}^T{\Sigma }_l^{-1}(\mathbf{x}-{\mathbf{\mu }}_l)$$
   把最后使得${\psi }_l(\mathbf{x})$最大的类别$l$做为最终所判为的类别，展开${\psi }_l(\mathbf{x})$有关于类别方差${\Sigma }_l^{-1}$的项${\mathbf{x}}^T{\Sigma }_l^{-1}\mathbf{x}$，所以它是二次判别式，在判别分析中称为二次判别分析。

3. 边界：类别$l$和$l^{\prime }$之间的边界由${\psi }_l(\mathbf{x})={\psi }_{l^{\prime }}(\mathbf{x})$给出. 边界关于$\mathbf{x}$是二次的。

参数估计:

简要提及一下参数分析，这主要设计到数理统计中的均值和方差估计的内容。

1. 一元均值$\mu$使用样本的均值来估计；多元均值${\mathbf{\mu }}_l$使用样本向量的均值来估计；

2. 类别$l$出现的先验概率使用频率来估计（这其实也是大数定律的内容）；

3. 单个总体的方差的估计使用样本方差来估计；总体的方差由所有类别构成的样本的方差由各个类别的样本方差加权和来估计，其中权数是某个类别总体的自由度除以样本总体的自由度。

简单写一下关于总体方差的估计：

首先在一个总体中有两个类别总体时，使用的估计是
$$\tilde{S}=\frac{n_1-1}{n_1+n_2-2}{S}_1^2+\frac{n_2-1}{n_1+n_2-2}{S}_2^2$$
推广到多个类别（假设$K$个）时，利用样本方差来估计总体方差：
$$\tilde{S}=\sum _{l=1}^K\frac{N_l-1}{N-K}{S}_l=\frac{1}{N-K}\sum _{l=1}^K\sum _{i\in C_l}({\mathbf{x}}_i-{\bar{\mathbf{x}}}_l)({\mathbf{x}}_i-{\bar{\mathbf{x}}}_l{)}^T$$

Naive Bayes

简介：朴素贝叶斯是一个有监督的分类方法。它适用于因变量是名义变量的情形，它对自变量类型没有限制。

现实应用：文本分类、广告及垃圾邮件过滤。

假设：在确定的某一类下，所有样本之间的观测是相互独立的，也就是在确定$Y$值之后，$X_1,\cdots ,X_p$是条件独立的。条件独立，则可以将这些样本的联合分布使用卷积公式展开。因此，可以对属于类被$Y=l$的观测，自变量$X=(X_1,\cdots ,X_n)$的概率函数或概率密度函数$f_l(\mathbf{x})$可以写成：
$$f_l(\mathbf{x})=f_l(x_1,\cdots ,x_n)=\prod _{r=0}^p{f}_l(x_r)$$
其中$f_l(x_r)$是类别$l$中自变量$X_r$的边缘分布。

算法：

自变量的取值一般有两种情况，一个是名义型变量，即分类型自变量；另一种是数值型变量，即连续变量

首先利用训练数据对自变量的概率取值和因变量的先验概率作估计，训练数据集属于类别$l$的观测中$X_r$取值为${\gamma }_v$的比例为
$${\hat{f}}_l(x_r={\gamma }_v)=\frac{\#[i:i\in C_{l}and{x}_{ir}={\gamma }_v]}{N_l}$$
但是一般是用样本某类出现的频率来估计某类出现的概率的话，如果某一变量取某值的频率为0，那么由假设的条件独立性知这个变量出现的概率为0，这样可能因为样本出现的随机性可能会对总体的估计造成严重的误差，所以我们考虑在分子和分母上各加上一个产生常数$n_0$，即使用一种更让平滑的估计：
$${\hat{f}}_l(x_r={\gamma }_v)=\frac{\#[i:i\in C_{l}and{x}_{ir}={\gamma }_v]+n_0}{N_l+V_{n_0}}$$
在得到以上概率分布的估计之后，计算出$P(Y=l|X=\mathbf{x}),l=1,\cdots ,K$的取值.

判别函数:$f(x)=arg\underset{l}{\max }P(Y=l|X=\mathbf{x})$，即使得$P(Y=l|X=\mathbf{x}),l=1,\cdots ,K$最大的类别$l$.

实例分析

iris 判别分析

判别分析的步骤：

1. 对总体的假设进行检验

   检验有两个，首先对总体进行正态性检验，在此基础上进行方差齐性检验。

   首先进行正态性检验：先画出数据的柱状图，初步查看数据的分布状况：

   可以看出，变量Speal.Length和Speal.Width是近似呈现正态分布的，Petal.Length和Petal.Width右半部分呈现出正态分布，但是左半部分频数呈现出一种下降的趋势。虽说变量Petal.Length和Petal.Width和不显然的呈现正态分布，但是他们的分布图形是相似的，且近似呈现出正态分布的。

   接下来继续对这些总体进行正态性检验，这里我们使用的检验方法是K-S检验，结合QQ图检验来近似判断每个变量是否服从正态性。

   首先通过K-S检验，找到所有变量检验的p值：

   Sepal.Length	Sepeal.Width	Petal.Length	Petal.Width
   0.1891	0.07023	1.532e-05	0.0002565

   若将显著性水平设置为0.05，则前两个变量p值均大于0.05，拒绝原假设，变量呈现近似正态分布。对于后面两个变量，根据散点图初步分析知他们近似呈现正态分布，所以我们再进一步地画出QQ图，如下面两图所示，可以近似地将后两个变量Petal.Length和Petal.Width看作是正态分布。
   

   方差齐性检验：这里使用F检验，得到

   setosa与versicolor	versicolor 与virginica	setosa与virginica
   0.1585	0.0009219	0.04069

   其中如果将显著性水平设置为0.01，setosa与versicolor ，setosa与virginica的p值均大于0.01， versicolor 与virginica的p值小于0.01, 两者方差有明显差距，但是总体上可以认为他们之间的方差是相等的，所以近似认为他们是方差齐性的。

2. 若检验通过，则对总体进行判别分析

   得到结果如图，其中有50个被判给了setosa类，49个被判为versicolor类；51个被判为Virginica类。下面继续对判别分析得到的结果进行分析。

3. 分别判别分析的结果，对结果作出解释

   得到混淆矩阵：
   

   对于混淆矩阵，行代表是真实值的类别，列代表预测的列别。由本次分析得到的混淆矩阵可知，使用判别分析的效果很好。其中将setosa类全部都判为了setosa类；关于versicolor有2个被错误判别了为virginica；Virginica有1个被错判给了versicolor。

wine-Naive Bayes分类

贝叶斯分类的步骤：

1. 首先查看数据的分布：

   从整体上看，所有的变量分布比较均匀，且没有缺失值。

2. 再对假设进行检验，即当在某一类确定的情况下，样本之间的分布是否独立。

   首先使用随机抽样的方式从13个变量中随机抽取3个变量之间的散点图分布：

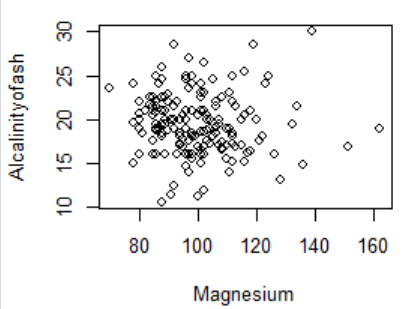   图1 Magnesium与Alcalinityofash

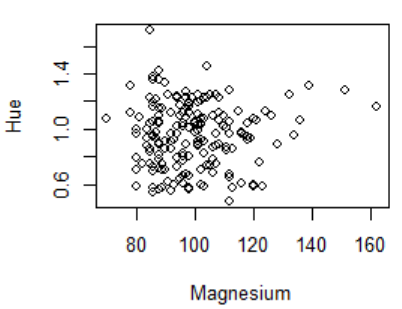   图2 Magnesium与Hue

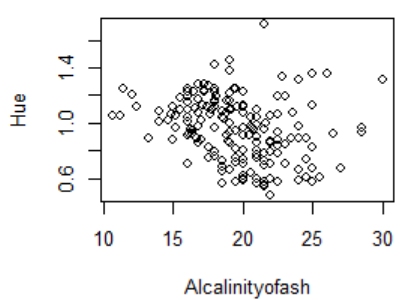   图3 Alcalinityofash与Hue

   有上三个图可知，变量之间没有明显的规律性，所以可以简单的认为数据之间是独立的。关于使用统计意义上的方法来检验数据之间的独立性，还有待继续探索。因为这里考虑到所有的4个自变量均是连续性变脸，一般意义上的卡方检验就不适用了，加上我暂时没有找到比较好的方差齐性检验的方法，故先简单认为不同类别下，变量之间是相互独立的。

   所以开始对数据进行贝叶斯分类分析。

3. 对原始数据进行贝叶斯分类分析。

   得到分类结果如上图所示。接下来结合原始数据来对拟合的结果进行分析。

4. 分析分类的结果，并且作出解释。
   

   如图所示，可知Naive Bayes对wine数据的分类效果也比较好，样本的个数比iris变量的个数更多，但是分类效果却比iris更好。其中第3类样本分类完全正确；第1类样本只有1个被错误分给了第2类；第2类样本只有也只有一个被错分给了第3类。

学习同学的

1. 大部分的模型，只要不过分违背基本假设，都可以尝试着使用相关的模型。
2. 当检验变量的独立性的假定时，可以先使用热力图查看变量之间的相关性。可以(a) 查看热力图，(b) 对变量之间相关系数比较小的，可以认为变量之间时独立的。因为在满足正态性的条件下，变量之间的独立性与相关系数对应。
3. 样本不平衡，使用过采样（当样本小，使用bootstrap)，来平衡数据。
4. 使用数据分析的步骤来搞，可以在进行模型评价的时候不仅使用，混淆矩阵、准确率。还要有进行模型的验证，即使用交叉验证来检验模型的效果。

总结

本文首先按照数据介绍、原理解释，加上实例分析对来分析总结某些分类方法的分类情况，综合结果得出，判别分析方法和朴素贝叶斯方法的分类效果都比较好。由于原来的数据量都比较小，且总体上基本都满足各自使用模型的假定，比如说判别分析的正态性假定以及朴素贝叶斯的某类下样本的条件独立性假定等。这正说明了课本上的一句话：越简单的模型在实际中的分析效果可能越好。因为一般的总体很多都是现实生活中比较随机的数据，其中难免会有一些比较极端值的情况，使用一些复杂的模型，即便是我们使用了非常好的特征工程处理，也很难达到非常好的预测效果。所以以后这些简单模型的分类效果很好，以后在尝试使用复杂模型受挫时，不妨回来看看简单的模型。

参考

[1] R语言学习笔记一：正态性检验与判断_雾都来的小屁孩的博客-CSDN博客_r语言正态性检验

[2] R语言–正态性检验 - 知乎 (zhihu.com)

[3] 【R】正态检验与R语言

[4] 有没有检验两个连续随机变量独立性的方法？ - 超理论坛 (chaoli.club)

代码

R语言：

library(MASS) # lda函数
# 验证算法是否满足假定条件

# 1、检验自变量是否满足正态分布
# (a)初步：画散点图
library(ggplot2)
hist_plot = function(x, col){
  hist(x,
       xlab = col,
       main = paste("Histogram of ", col),
       col="grey")
}

col = colnames(iris)
par(mfrow = c(2, 2))
hist_plot(iris[, 1], col[1])
hist_plot(iris[, 2], col[2])
hist_plot(iris[, 3], col[3])
hist_plot(iris[, 4], col[4])

# 进一步：k-s正态性检验
library(dbplyr)
scale(iris[, 1]) %>% ks.test(pnorm)
scale(iris[, 2]) %>% ks.test(pnorm)
scale(iris[, 3]) %>% ks.test(pnorm)
scale(iris[, 4]) %>% ks.test(pnorm)

# 后两个变量qq图
qqnorm(iris[, 3])
qqline(iris[, 3])
qqnorm(iris[, 4])
qqline(iris[, 4])

# (b)方差齐性检验，F检验
c1 = iris[iris[, 5]=="setosa",]
c2 = iris[iris[, 5]=="versicolor", ]
c3 = iris[iris[, 5]=="virginica", ]
table(iris[, 5])

var.test(cov(c1[, 1:4], c1[, 1:4]), cov(c2[, 1:4], c2[, 1:4]))
var.test(cov(c1[, 1:4], c1[, 1:4]), cov(c3[, 1:4], c3[, 1:4]))
var.test(cov(c2[, 1:4], c2[, 1:4]), cov(c3[, 1:4], c3[, 1:4]))

# 2、判别分析
# 线性判别分析
lda_iris <- lda(iris$Species~.,data=iris)

# 预测
pre_lda_iris <- predict(lda_iris,iris)
table(pre_lda_iris$class)
table(iris$Species)

# 混淆矩阵
lda_conmat <- table(iris$Species,pre_lda_iris$class)
lda_conmat



#############Naive bayes
# 1、读取数据
path = "D:/lagua/CODING/R-learn/R-code/Chap7_PredictiveAnalysis/ch7_wine.csv"
wine = read.csv(path)
colnames(wine) <- c("cultivers","Alcohol", "Malicacid", "Ash", "Alcalinityofash", "Magnesium",
                    "TotalPhenols", "Flavanoids", "NonflavanoidPhenols",
                    "Proanthocyanins", "ColorIntensity", "Hue",
                    "OD280OD315", "Proline")
# 查看分布
summary(wine)

# 2、查看条件变量之间是否相互独立
library(ggplot2)
# 初步：这里画散点图
plot(wine)
col = colnames(wine)
x <- sample(2:14, 3)
x = c(6, 5, 12)
plot(wine[, x[1]], wine[, x[2]], xlab=col[x[1]], ylab=col[x[2]])
plot(wine[, x[1]], wine[, x[3]], xlab=col[x[1]], ylab=col[x[3]])
plot(wine[, x[2]], wine[, x[3]], xlab=col[x[2]], ylab=col[x[3]])


library(e1071)
# 因变量类型转化
wine$cultivers <- as.factor(wine$cultivers)

# 3、用朴素贝叶斯算法进行分类
NB_wine <- naiveBayes(wine$cultivers~.,data=wine)

# 进行预测 
pre_NB_wine <- predict(NB_wine,wine)
table(pre_NB_wine)

# 混淆矩阵
#wine$Class为实际类别，pre_NB_wine为预测类别
NB_conmat <- table(wine$cultivers,pre_NB_wine)
NB_conmat