矩阵奇异值分解(SVD)
- 奇异值分解(Singular Value Decomposition)是一种重要的矩阵分解方法,可以看作对称方阵在任意矩阵上的推广。
- 假设A是一个m*n阶实矩阵,则存在一个分解使得:

SVD的不足
上面我们举了例子,SVD是很粗暴的将数据的特征值排一个序,然后选取最大的几个特征值来代表原数据的特征,这在图像处理方面确实没有问题,因为图像存储在电脑中说白了就是一堆灰度值点而已,它们之间是没有联系的,单纯的提取最有特点的部分是没有问题的。
但是!但是!但是!
许多的数据集中,每个数据的属性之间是有联系的!如此一来,单纯的提取特征的手段得到的效果必然是不会好的,所以我们得对SVD进行加强!于是我们的PCA闪耀登场!
主成份分析(PCA)
上述说了SVD不能考虑属性间关联的缺陷,所以我们得解决这个问题,如何才能表示属性间的关联呢?回想数理统计的知识,是不是想到了协方差!
没错!属性间的协方差就能表达属性间的联系!
如此一来,我们得到数据之后不直接对其进行SVD了,我们要做一些“预处理”,我们先求各个数据的协方差矩阵!
比如我们有个3维的数据(x,y,z),那么协方差矩阵是:
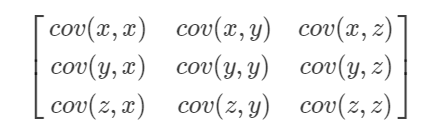
然后我们通过这个协方差矩阵求得SVD方法中的矩阵U与V,然后再根据求出的U与V去用SVD的原理提取原数据的特征就行了。这样我们的“提取规则(也就是矩阵U和V)”是考虑了原数据属性间的联系而制定的,弥补了SVD的缺陷。
很显然,其实PVA就是考虑了原数据的属性间的联系的SVD。
PCA,ICA和CCA
1.PCA
m个n维的样本数据X1,X2,...,XmX1,X2,...,Xm, 均值为u
步骤:
(1)标准化, Xi−uXi−u
(2)计算协方差矩阵 E{(X−E(X))(X−E(X))T}E{(X−E(X))(X−E(X))T}
(3)计算特征值和特征向量(单位化)
(4)选择特征值最大的前k(1≤≤k≤≤n)项的特征向量
(5)利用特征向量的组合进行线性变换,得到新的数据2.ICA 独立成分分析
3.CCA 典型相关分析








 本文详细介绍了矩阵奇异值分解(SVD)及其在图像处理中的应用,并指出其在处理具有属性间联系的数据集时的局限性。进而引入主成分分析(PCA)作为改进方案,通过计算数据集的协方差矩阵来考虑属性间的联系。
本文详细介绍了矩阵奇异值分解(SVD)及其在图像处理中的应用,并指出其在处理具有属性间联系的数据集时的局限性。进而引入主成分分析(PCA)作为改进方案,通过计算数据集的协方差矩阵来考虑属性间的联系。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










