完全背包问题
题目
有N NN种物品和一个容量为V 的背包,每种物品都有无限件可用。第i ii种物品的费用是w[i] ,价值是v[i] 。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
基本思路
这个问题非常类似于01背包问题,所不同的是每种物品有无限件。也就是从每种物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0 00件、取1 11件、取2 22件……等很多种。如果仍然按照解01背包时的思路,令f[i][j] 表示前i 种物品恰放入一个容量为V 的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程,像这样:
![]() j是背包的体积
j是背包的体积
一个简单有效的优化:
剔除价值小费用高的物品,大于V的剔除,然后用计数排序的方法计算处相同物品中价值最高的那个。来优化
分治算法

学习链接
https://blog.csdn.net/boshuzhang/article/details/77896250
https://blog.csdn.net/Loving_Forever_/article/details/54092926
<1. 什么是分治算法?
- 分解(Divide)将大规模的问题分解成若干个规模更小但形式相同的子问题
- 解决(Conquer)如果当前问题的规模足够小,并可以直接解决的话,那么直接解决并返回解。否则,继续进行分解并递归求解分解后的子问题。
- 合并(Merge)将各个子问题合并,最终形成原问题的解。
分成两个相同或者相似的子问题,再把子问题分成更小的问题,一直这样下去.......直到最后,子问题可以简单地求解,还有一点就是把所有求得的子问题合并就是原问题的解。其实在很多场合下都会使用到分治算法,比如说我们常用的归并排序、快速排序都是很常见的分治思想的体现。
<2. 核心思想: 把大问题分解成小问题,逐个击破。

<3. 分治的适用场景

<4. 实际运用:
类似于数学归纳法,找到解决本问题的求解方程公式,然后根据方程公式设计递归程序。
第一步:一定是先找到最小问题规模时的求解方法,一般来说最小问题规模的求解方法是很简单的(就像归并排序之中当问题规模最小的时候,也就是只有一个元素的时候,直接就已经有序了)。
第二步:然后考虑随着问题规模增大时的求解方法,区间划分完了之后,开始考虑规模增大之后应该怎么做,还是以归并排序为例,当划分到每一个元素之后,不能再往下划分了,这时候就需要考虑问题增大时候的求解方法,增大具体方法需要借助另外一个存储空间,这也是归并排序为什么需要O(N)的额外存储空间。
第三步:找到求解的递归函数式后(各种规模或因子),设计递归程序即可。
//---------------------------归并排序之中问题增大时候的求解方法---------------------------------
void Merge(int sourceArr[], int tempArr[], int startIndex, int midIndex, int endIndex)
{
int i = startIndex, j = midIndex + 1, k = startIndex;
while (i != midIndex + 1 && j != endIndex + 1)
{
if (sourceArr[i] >= sourceArr[j])
tempArr[k++] = sourceArr[j++];
else
tempArr[k++] = sourceArr[i++];
}
while (i != midIndex + 1)
tempArr[k++] = sourceArr[i++];
while (j != endIndex + 1)
tempArr[k++] = sourceArr[j++];
for (int index = startIndex; index <= endIndex; ++index)
sourceArr[index] = tempArr[index];
}
//---------------------------------归并排序划分为子问题------------------------------------------
void MergeSort1(int sourceArr[], int tempArr[], int startIndex, int endIndex) //内部递归使用
{
int midIndex = 0;
if (startIndex < endIndex)
{
midIndex = startIndex + (endIndex - startIndex) / 2;
MergeSort1(sourceArr, tempArr, startIndex, midIndex);
MergeSort1(sourceArr, tempArr, midIndex + 1, endIndex);
Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
}
}
//----------------------------------------优化方法---------------------------------------------
void MergeSort2(int sourceArr[], int tempArr[], int startIndex, int endIndex)
{
int midIndex = 0;
if ((endIndex - startIndex) >= 50) // 大于50个数据的数组进行归并排序
{
midIndex = startIndex + (endIndex - startIndex) / 2;
MergeSort2(sourceArr, tempArr, startIndex, midIndex);
MergeSort2(sourceArr, tempArr, midIndex + 1, endIndex);
Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
}
else // 小于50个数据的数组进行插入排序
InsertSort(sourceArr + startIndex, endIndex - startIndex + 1);
}青蛙
首先,当青蛙在面对第一个台阶时,他只有两种选择——跳一步还是跳两步。如果我们定义f(n)代表青蛙跳跃到n层台阶一共的方法数,那么我们可以将问题进行分解两个规模更小,但形式相同的问题:
| 1 |
|
其中f(n - 1)是青蛙选择跳一步后,剩下的子问题,同理f(n - 2)是青蛙选择跳两步后剩下的子问题。这样,我们就把问题进行了分解。
下面再谈谈如何解决,正如上面谈到的解决步骤,如果规模足够小那么直接返回,否则继续降低规模进行递归求解。这时,就是我们要确定边界条件——即当n = 1 和n = 2时的情况。、
如果没有到最小问题求解处,则f(n - 1) + f(n - 2)把问题分解成最小问题,再合并解
int f(int n) {
// 边界条件(解决)
if (n < 1) return 0; // 当台阶数目小于1时,那么就返回0种方案数量
if (n == 1) return 1; // 当台阶数目为1时,问题的规模已经足够小,我们可以直接想出他的方案数量—— 即1种:1步
if (n == 2) return 2; // 当台阶数目为2时,他的方案数量为2种,即—— 1步+1步,2步
return f(n - 1) + f(n - 2); // 分解并合并 如果没有到最小问题求解处,则把问题分解成最小问题,再合并解
}
int main() {
cout<<f(4)<<endl;
return 0;
}
动态规划算法
<1 、什么是动态规划
关于什么是动态规划呢?用通俗一点的话来说就是“边走边看”,注意和回溯法这种先把一条道走到黑的方法区别开来,总的来说就是前面的知道了,后面的也可以根据前面的推导出来了。好了通俗的话说到这了,下面用正规一点的语言总结一下:每次决策依赖于当前状态,又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。
<2 、核心思想

由于动态规划解决的问题多数有重叠子问题这个特点,为减少重复计算,对每一个子问题只解一次,将其不同阶段的不同状态保存在一个二维数组中。

<3. 动态规划的适用场景
动态规划本质上来说还是规划,是不断进行决策的问题,一般用于求解最(优)值;而分治是一种处理复杂问题的方法,不仅仅只用于解决最值问题(而且我们一般也不用它来求最值,你想一串数字如果特别多,你想找一个最大的出来,用了一个排序是不是有一点奢侈呢,比较游戏与效率要求真的很高)。
动态规划来解决的问题,通常要满足以下三点要求:
(1)最优化原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
(2)无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
(3)有重叠子问题:即子问题之间是不独立的,一个子问题【或者子问题的解】在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
<4 、实际运用
“用”
动态规划所处理的问题是一个多阶段决策问题,一般由初始状态开始,通过对中间阶段决策的选择,达到结束状态。这些决策形成了一个决策序列,同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。动态规划的设计都有着一定的模式,一般要经历以下几个步骤。
初始状态→│决策1│→│决策2│→…→│决策n│→结束状态

一般,只要解决问题的阶段、状态和状态转移决策确定了,就可以写出状态转移方程(包括边界条件)。

动态规划的难点在于上述四个步骤的确立。

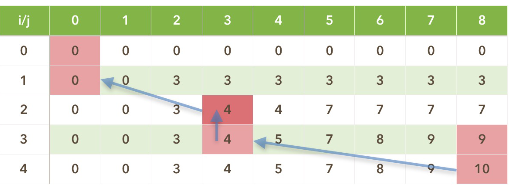
动态规划应用:
一、背包问题
https://blog.csdn.net/yandaoqiusheng/article/details/84782655 //看此博客
题目
有N 件物品和一个容量为V 的背包。第i件物品的费用是w[i](该i 物品需要占用的体积),价值是v[i],求将哪些物品装入背包可使价值总和最大。
基本思路
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
用子问题定义状态:即f[i][j] 表示前i 件物品恰放入一个容量为j 的背包可以获得的最大价值。则其状态转移方程便是:
f[i][j]=max(f[i−1][j],f[i−1][j−w[i]]+v[i])
分析问题:
【(1)分析最优解的性质 (2) 递归的定义最优解 (3)记忆法保存每个阶段的值[一般是二维数组] (4)根据计算最优解的时得到的信息构造问题的最优解 】
编码思路:
【(1)阶段划分 (2)确定状态和状态变量 (3)写出状态方程[根据相邻两个状态之间的关系来写] (4)寻找边界值 】

红线部分理解: 还是前i-1件物品。放入剩余容量为 j−w[i] 的背包中【因为此处的体积要减去第i件物品自身占用背包的体积】。而价值则需要在前 i-1 价值的基础上加上i件物品的价值。


上述代码只是举例说明情况【会越界】,下边的才是正确的 j>=w[i]
第i 件物品的费用是w[i] 【该i 物品需要占用的体积】,保证背包中的剩余体积是 j >=放入该物品需要的体积。则:

初始化的细节问题:
我们看到的求最优解的背包问题题目中,事实上有两种不太相同的问法。有的题目要求"恰好装满背包"时的最优解,有的题目则并没有要求必须把背包装满。这两种问法的区别是在初始化的时候有所不同。
//参考链接 https://www.cnblogs.com/Christal-R/p/Dynamic_programming.html



using System.Collections;
using System.Collections.Generic;
using UnityEngine;
/// <summary>
/// https://www.cnblogs.com/Christal-R/p/Dynamic_programming.html
/// </summary>
public class Bag : MonoBehaviour
{
int capacity = 8; //包的体积
int number = 4; //物品个数
int[] w = new int[] { 0,2, 3, 4, 5 }; //物品的体积
int[] v = new int[] { 0,3, 4, 5, 6 }; //物品的价值
int[,] V = new int[4+1,8+1]; //因为从i=1开始的,所有这个表需要+1(i,0)=0 (0,j)=0
int maxValue; //最优解
private void Start()
{
FindMax();
}
void FindMax()//动态规划
{
int maxI=0, maxJ=0;
int i, j; //i第i个商品 j是背包的体积
//填表
for (i = 1; i <= number; i++)
{
for (j = 1; j <= capacity; j++)
{
if (j < w[i])//包装不进,包的体积<物体的体积
{
V[i,j] = V[i - 1,j];
//Debug.Log(i + " " + j + " " + V[i, j]);
}
else//能装的情况下,取一个价值更大的装进去
{
#region
//考虑最大价值的情况下
//if (V[i - 1, j] > V[i - 1, j - w[i]] + v[i])//不装价值大
//{
// V[i, j] = V[i - 1, j];
// Debug.Log(i + " " + j + " " + V[i, j]);
//}
//else//前i-1个物品的最优解与第i个物品的价值之和更大
//{
// V[i, j] = V[i - 1, j - w[i]] + v[i];//****
// Debug.Log(i + " " + j + " " + V[i, j]);
//}
#endregion
//返回价值更大的值
V[i, j] = Mathf.Max(V[i - 1, j], V[i - 1, j - w[i]] + v[i]);
//Debug.Log(i + " " + j + " " + V[i, j]);
if (maxValue < V[i, j])
{
//知道装不下时 ,背包中的价值最大是10,即最优解是10
maxValue= V[i, j];
maxI = i;
maxJ = j;
}
}
}
}
FindWhat(maxI, maxJ);
}
//根据最优解回溯找出解的组成表格填完,最优解即是V(number,capacity)=V(4,8)=10,即获得的最大价值是10
//但还不知道解由哪些商品组成,故要根据最优解回溯找出解的组成,
//根据填表的原理可以有如下的寻解方式
void FindWhat(int i, int j)//寻找解的组成方式,根据填表的原理
{
if (i >0)
{
if (V[i,j] == V[i - 1,j])//相等 根据最优解回溯 如果V(i,j)=V(i-1,j)时,
//如果商品在装(i-1)个商品时背包中的价值是num (num=5) ,在i时任然等于n(5),则说明在i时就没装
{
FindWhat(i - 1, j);
}
else if (j - w[i] >= 0 && V[i,j] == V [i - 1 , j - w[i]] + v[i])
{
Debug.Log("装进去的商品序号 "+i);
FindWhat(i - 1, j - w[i]);//回到装包之前的位置
}
}
}
// //void FindMaxBetter()//优化空间后的动态规划
// //{
// // int i, j;
// // for (i = 1; i <= number; i++)
// // {
// // for (j = capacity; j >= 0; j--)
// // {
// // if (B[j] <= B[j - w[i]] + v[i] && j - w[i] >= 0)//二维变一维
// // {
// // B[j] = B[j - w[i]] + v[i];
// // }
// // }
// // }
// //}
}
树的遍历查找法:更新每次的价值,找到最大价值,可以直接找到最大价值的父节点对应的物体。

树转成二叉树,再使用堆遍历。例如:大顶堆 跟节点最大、左、右结点次之。二叉搜索树:左<跟节点 右>根节点 ,方便动态搜索。
青蛙问题动态规划求解:
最优子结构
如果一个问题的最优解包含了其中子问题的最优解,那么称其具有最优子结构的性质。
什么意思?青蛙在面对n个台阶时的解决方案数是f(n),那么我们知道f(n) = f(n - 1) + f(n - 2)。其中的f(n - 1)与f(n - 2)就是两个子问题的最优解,此时我们可以理解成一个问题的最优解包含了其子问题的最优解,那么这个时候这种问题具有了最优子结构性质。
重叠子问题
这个性质,在我理解是对于上文提到的子问题的补充说明。当解决一个问题时,往往需要依赖于其更小规模的子问题的解,甚至是同时依赖于若干个规模更小的子问题的解,即子问题是被(重复)包含于比其更大的问题中的,所以他是具有重叠子问题的性质。
在这里,多提出一句,这个子问题是在解决当前问题时需要依赖的。即,只有计算了子问题,父问题才可能被求解。这是和贪心算法的重要区别所在。
状态转移方程
| 1 |
|
- i代表当前问题的规模,即所需要跳过的台阶数。
- dp[i]代表的是跳过i个台阶的方案数量
int n = 4;
vector<int> dp(n + 1, 0);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i < = n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
cout<<dp[n]<<endl;
return dp[n];
贪心算法
所谓贪心就是总是在当前情况下做出最为有利的选择,也就是说它不从整体上考虑。它只是做出了某种意义上的局部最优解。
贪心算法不像动态规划那样有固定的框架,由于贪心算法没有固定的算法框架,因此怎么样区分有关于贪心算法呢?这就需要一种贪心策略了!贪心算法不是所有情况下都能得到整体最优解,得到的只是一个近似最优解,所以求最值的问题上,一般不用贪心算法,而是用动态规划算法。贪心策略的选择必须满足无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。
二、核心思想
关于贪心算法,其实没有过多要说的,就简单说一下步骤吧!
第一步:建立数学模型来描述问题。
第二步:把求解的问题分成若干个子问题。
第三步:对每一子问题求解,得到子问题的局部最优解。
第四步:把子问题的解局部最优解合成原来解问题的一个解。
三、贪心算法的适用场景
贪心策略的前提就是尽量保证局部最优解可以产生全局最优解,最美好的贪心策略当然就是希望能通过不断地求局部最优解从而得到全局最优解!
如:上面的背包问题,并不能用弹贪心算法。因为贪心算法只能从某一个方向考虑,比如单单以重量(每次选择重量最轻的),或用价值(每次选择价值最高的),甚至用价格与重量的比值,其实这三者都实际运用过程之中都有问题,基本很难得到最优解。
四、实际运用
寻路
同时使用路径搜索和运动算法。
我们每次都从 "开启列表" 找出 F 值最小的, 将它从 "开启列表" 中移掉, 添加到 "关闭列表".。再继续找出它周围可以到达的方块,如此循环下去...
用一个实例来完全理解A*寻路算法
<1.
取起始点加入到OPen中。
考察这个点相邻的八个点【即计算相邻点的f,g,h】,检查完后把这个起始点加入到Close中 .
记录每个节点的连接,即当前位置之前经过的那个节点。
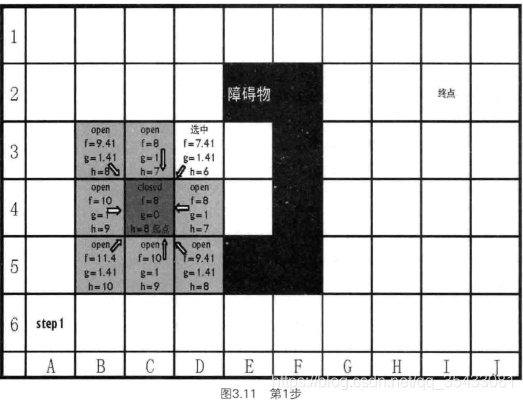
<2.
计算Open表中8个节点的行走代价,选择最小的作为这一轮的查考对象.
计算从起始点移动到当前点的移动代价(记录为g),还要计算当前到目标点的代价(h),总移动代价f=g+h.
计算g: 取它父节点的g,以找相对于父节点的连接方式,增加相应的值。例如:对角线连接,增加1.414,直线连接增加1.(或者 根据和父节点的连接关系。算出节点走回到起始位置所需要的移动代价)。
计算h: 由于没有到达目标点,所以只能估算h,即启发方式,采用欧立德几何【两节点之间的距离】或者曼哈顿距离等。此处采用曼哈顿距离。即当前格子到目标点。先水平后垂直方向的数量和作为h的估算值。【假设没有障碍物的情况】
计算f=g+h.首先应该检查移动代价最低的那些节点(第一步图中的选中)。如果有多个节点最有相等的最小值,可以任选一个进行检查。
以上步骤结束后,则选中(3,D)为代价最小的节点,接下来检查这个节点:障碍物无需检查,其他七个节点中3个已经在Open或者Close中,但是之前记录的g值是通过其他路径得到的,因此本轮需要再次计算通过当前节点(3,D)所得到的新g值。见第2步图示。检查结束后,把(3,D)加入到Close中。

<3.
首先检查Open表,找出其中具有最低代价的节点,即(3,E),(2,D),选择任意一个,例如(3,E),且相邻节点也不需要更新信息,把这个节点加入到Close中。

<4.
上图中,再次检查Open表,选中最低代价节点(2,D),检查8个相邻点,(2,C)、(3,C)在Open表中;(3,D)、(3,E)在Close中,检查后无需更新信息。对于(1,E)因为有障碍物(2,E)的存在,因此不是直接到达的。检查(1,C)和(1,D)。 此时相邻点检查完毕,将(2,D)d点移出Open,加入Close中。

<5.
上图,检查Open,任意选择一个最小代价的,即(3,C)进行检查其相邻点。更新需要更新的g,h ; 并且这个点的父节点变为(3,C) ;
再计算还没进行检查的点(2,B)的g,h,把它加入到Open中。相邻节点检查完毕后,把它移入到Close中。
下图所示:
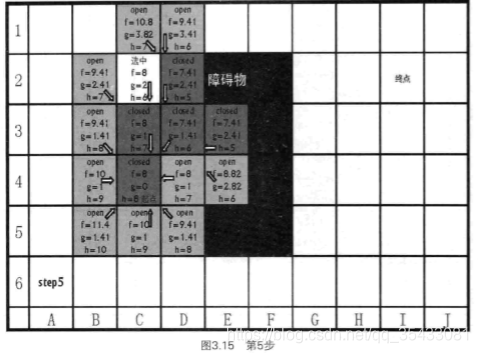
重复上述步骤,直到目标点也进入到Open中,沿着箭头回溯,找到从起点到目标点的路径。箭头方向看向选中点,注意对于Open表中重复的相邻点的箭头方向是不更新,只更新g,h。
最终得到下图:

四、 回溯法、
一、什么是回溯算法
回溯法也称试探法,它的基本思想是:从问题的某一种状态(初始状态)出发,搜索从这种状态出发所能达到的所有“状态”,当一条路走到“尽头”的时候(不能再前进),再后退一步或若干步,从另一种可能“状态”出发,继续搜索,直到所有的“路径”(状态)都试探过。这种不断“前进”、不断“回溯”寻找解的方法,就称作“回溯法”。满足回溯状态的某个点就称之为“回溯点”。
应用:迷宫问题之中我们就可以使用回溯法求解!回溯法可以说是一种优选搜索法,按照选优条件向前搜索,以求最后达到最终的目标,假如是在迷宫问题之中如果达到出口的时候,那么回溯的过程也就结束了。达不到目的地,也就是所说的碰到了“障碍物”。那么这时候它就会退回一步重新选择,这种走不通就回退一步的再走的技术为回溯法,而满足回溯状态的某个点就称之为“回溯点”。
二、核心思想
接下去再来说一说回溯法的核心思想,在包含所有问题的解空间树之中,按深度优先搜索的策略,从根节点出发深度搜索解空间树。当搜索到某一个节点的时候,先检测当前点是否满足条件,如果满足就从该节点出发继续搜索下去,否则不满足那么就逐层向其祖先节点进行回溯。其实也就是深度优先策略,首先从根节点出发深度搜索解空间树。当搜索到某一个节点的时候,这时候需要判断该节点是否包含问题的解,如果包含,就从该节点继续出发搜索下去,如果该节点不包含问题的解,那么这时候就逐层向根节点进行回溯。
回溯法: 就是对隐式图的深度优先搜索算法,先一条道走到黑,走到不能走时,再回溯到上一步重新选择。
贪心算法:每一步都找最优的解,且每一步都找能走的节点【路】,每一步决策时互相独立,无后效性。
动态规划:每一步都会影响到下一步的决策,且有后效性。
【
隐式图:仅给出初始结点、目标结点以及生成子结点的约束条件(题意隐含给出),根据扩展规则,不停的扩展结点,直到扩展节点中包含目标节点的过程。(例如: 对于回溯法只要没有障碍物就成,而A*还要考虑路径代价)。
算法: 启发式搜索(A*)
结点扩展次序受问题的性质和目标结点的一般方向的影响,扩展结点时要估计由初始结点经结点至目标结点的路径代价。它只需要产生全部的状态空间的部分结点及相互关系就可以求解问题了,因此搜索效率高。
】
回溯方法求解问题的所有解的时候,如果没有找到最终的目标,那么只有当回溯到根节点的时候才可以,并且根节点的所有可行子树都要已被遍历才可以。但是通常我们只需要某一个解就行了,比如在走迷宫的时候我们只需要找到一个出口就行了(假设迷宫有多个出口)。
三、回溯算法的适用场景
那么什么时候需要用到回溯算法呢?首先使用回算法的时候需要注意一下,需要明确定义问题的解空间,问题的解空间至少包含问题的一个最优解。
在使用的时候我们还需要确定节点的扩展搜索规则,以深度优先方式搜索解空间,并且你还可以在搜索过程之中利用剪枝函数避免无效的搜索。
四、实际运用
具体运用,首先来看一下算法的框架。假设一个问题的解是一个n维向量(a1,a2,a3,....,an),约束的条件是ai(i = 1,2,3,.....,n)之间满足某种条件,并用一个函数式f(ai)来表示。
说了怎么表示之后,我们就需要用把整个框架搭出来。一般来说有两种常见的方法,一种是递归解法,一种是非递归解法,下面我们就把这两种框架写出来。
回溯法框架:
非递归算法框架:
int a[n], i; //n是一个常量,初始化数组
i = 1;
while(i > 0 && (还没有达到出口,即还有路可以走)) //表示还没有回溯到头
{
if( i > n) //已经搜索到最终叶子节点
{
//已经搜索到了解,可以进行输出了
//如果不需要搜索出所有的解,这时候就可以结束退出了
}
else
{
//a[i]第一个可能的值
while(a[i]在不满足约束条件且在搜索空间之内)
{
a[i]下一个可能的值
}
if(a[i]在搜索空间之内)
{
//此时作为技术功能的i需要进行++操作,表示资源的占用
i = i +1;
}
else
{
清理所占的状态空间; // 回溯
i = i –1;
}
}
}
递归框架:
一般来说回溯法还是使用递归方式解决比较好,因为回溯法是对解空间的深度优先搜索,用下面的伪代码来简单模拟实现一下:(k表示搜索的深度)
int a[n];
try(int i)
{
if(i>n)
输出结果;
else
{
for(j = 下界; j <= 上界; j=j+1) // 枚举i所有可能的路径
{
if(fun(j)) // 满足限界函数和约束条件
{
a[i] = j;
... // 其他操作
try(i+1);
回溯前的清理工作(如a[i]置空值等);
}
}
}
}
使用回溯方法解决的具体问题:
树的深度优先算法。
/**
* int count 方案总数
* int target 目标—— 剩余的台阶数
*/
void dfs(int& count, int target) {
// 边界条件
if (target < = 2) {
count += target; // 当剩余一个台阶是即累加一种方案,剩余两个台阶时累加两种方案
return;
}
// 下面是两个基本点选择一步和选择两步
// 选择一步
dfs(count, target - 1);
// 选择两步
dfs(count, target - 2);
}
int main() {
int count = 0;
dfs(count, 4);
cout<<count<<endl;
return 0;
} 
五:分支界限法
























 2358
2358











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








