kappa与quadratic weighted kappa

kappa系数是统计学中度量一致性的指标, 对于分类问题，一致性就是模型预测结果和实际分类结果是否一致. kappa系数的计算是基于混淆矩阵, 取值为-1到1之间, 通常大于0.

• kappa
• quadratic weighted kappa

kappa

kappa系数的数学表达:

Po​为预测的准确率, 也可理解为预测的一致性:

 

Pe​表示偶然一致性:

 

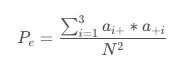
 例子来自：https://blog.csdn.net/weixin_38313518/article/details/80035094

 

quadratic weighted kappa

二次加权kappa在多级分类的深度学习评价中经常使用，比如说医疗图像的多级分类。人类医生在评判病症时经常用轻度，中度，重度等词汇，这样的评价方式与二次加权kappa的评价方式不谋而合，使用加权的kappa，可以有效反映模型的效果。

quadratic weighted kappa系数的数学表达如下，其中代表将第i类判别为第j类的个数，代表根据真实列联表根据上文提到的计算方法:

 

例子：

code：

conf_mat = confusion_matrix(rater_a, rater_b, min_rating, max_rating)

num_scored_items = float(len(rater_a))
d = pow(i - j, 2.0) / pow(num_ratings - 1, 2.0)
numerator += d * conf_mat[i][j] / num_scored_items

 

 code：

num_scored_items = float(len(rater_a))

expected_count = (hist_rater_a[i] * hist_rater_b[j]/ num_scored_items)
d = pow(i - j, 2.0) / pow(num_ratings - 1, 2.0)
denominator += d * expected_count / num_scored_items

end code:

1.0 - numerator / denominator

complete code:

def confusion_matrix(rater_a, rater_b, min_rating=None, max_rating=None):
    """
    Returns the confusion matrix between rater's ratings
    """
    assert(len(rater_a) == len(rater_b))
    if min_rating is None:
        min_rating = min(rater_a + rater_b)
    if max_rating is None:
        max_rating = max(rater_a + rater_b)
    num_ratings = int(max_rating - min_rating + 1)
    conf_mat = [[0 for i in range(num_ratings)]
                for j in range(num_ratings)]
    for a, b in zip(rater_a, rater_b):
        conf_mat[a - min_rating][b - min_rating] += 1
    return conf_mat

def histogram(ratings, min_rating=None, max_rating=None):
    """
    Returns the counts of each type of rating that a rater made
    """
    if min_rating is None:
        min_rating = min(ratings)
    if max_rating is None:
        max_rating = max(ratings)
    num_ratings = int(max_rating - min_rating + 1)
    hist_ratings = [0 for x in range(num_ratings)]
    for r in ratings:
        hist_ratings[r - min_rating] += 1
    return hist_ratings

def quadratic_weighted_kappa(rater_a, rater_b, min_rating=None, max_rating=None):
    """
    Calculates the quadratic weighted kappa
    quadratic_weighted_kappa calculates the quadratic weighted kappa
    value, which is a measure of inter-rater agreement between two raters
    that provide discrete numeric ratings.  Potential values range from -1
    (representing complete disagreement) to 1 (representing complete
    agreement).  A kappa value of 0 is expected if all agreement is due to
    chance.

    quadratic_weighted_kappa(rater_a, rater_b), where rater_a and rater_b
    each correspond to a list of integer ratings.  These lists must have the
    same length.

    The ratings should be integers, and it is assumed that they contain
    the complete range of possible ratings.

    quadratic_weighted_kappa(X, min_rating, max_rating), where min_rating
    is the minimum possible rating, and max_rating is the maximum possible
    rating
    """
    rater_a = np.array(rater_a, dtype=int)
    rater_b = np.array(rater_b, dtype=int)
    assert(len(rater_a) == len(rater_b))
    if min_rating is None:
        min_rating = min(min(rater_a), min(rater_b))
    if max_rating is None:
        max_rating = max(max(rater_a), max(rater_b))
    conf_mat = confusion_matrix(rater_a, rater_b,
                                min_rating, max_rating)

    num_ratings = len(conf_mat)
    num_scored_items = float(len(rater_a))

    hist_rater_a = histogram(rater_a, min_rating, max_rating)

    hist_rater_b = histogram(rater_b, min_rating, max_rating)

    numerator = 0.0
    denominator = 0.0

    for i in range(num_ratings):
        for j in range(num_ratings):
            expected_count = (hist_rater_a[i] * hist_rater_b[j]
                              / num_scored_items)
            d = pow(i - j, 2.0) / pow(num_ratings - 1, 2.0)
            numerator += d * conf_mat[i][j] / num_scored_items
            denominator += d * expected_count / num_scored_items

    return 1.0 - numerator / denominator

run code:

import quadratic_weighted_kappa as qw_kappa

rater_a = [0, 3, 4, 5, 2, 3, 4, 1, 2, 3, 5, 4, 3, 2, 4, 1, 0, 2, 3, 3]
rater_b = [2, 3, 4, 5, 2, 3, 2, 0, 2, 4, 5, 4, 3, 2, 4, 1, 0, 2, 3, 3]
result = qw_kappa.quadratic_weighted_kappa(rater_a, rater_b)
print("result:", result)