模拟退火学习笔记

模拟退火

来自百度百科：
模拟退火算法（Simulate Anneal，SA）是一种通用概率演算法，用来在一个大的搜寻空间内找寻命题的最优解。模拟退火是由S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在1983年所发明的。V.Čern&yacute在1985年也独立发明此演算法。模拟退火算法是解决TSP问题的有效方法之一。
模拟退火的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法，其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。

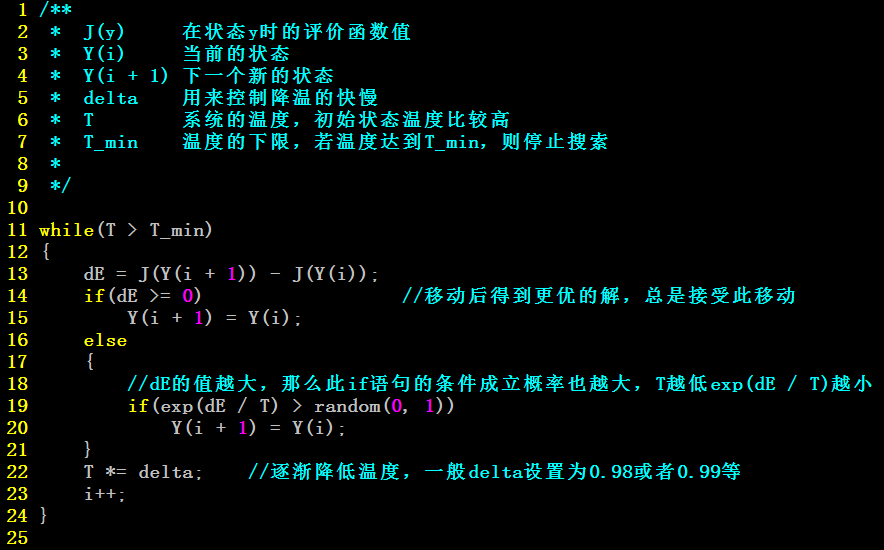
也就是说，在模拟退火中，有三个步骤：一是设定初始状态（初温T，温度阀值Tmin，温度下降速度delta），二是状态转移（若有更优解直接转移，按照当前温度大小，有一定概率接受一个更差的解），三是温度下降。

爬山算法也是一个解决最优化问题的算法，每次向着函数上升速率最快的方向走，但根据不同的初始位置，容易陷入不同的局部最优解，而模拟退火可以很好地避免这个问题。模拟退火是模拟热力学系统中的退火过程，将退火过程中的能量函数换成目标函数。

$$P_i(T_k)=C_k\times exp(-\frac{E_i}{T_k})$$
模拟退火算法也是贪心算法，但是在其过程中引入了随机因素，以一定的概率接受一个比当前解要差的解，并且这个概率随着时间的推移而逐渐降低。

若$J(Y_{i+1})>J(Y_{i})$，即移动后得到更优的解，那么总是接受改移动。
若$J(Y_{i+1})<J(Y_{i})$，即移动后得到更差的解，则以一定的概率接受该移动，并且这个概率随时间推移逐渐降低。
这个概率表示为:$P(dE)=exp(\frac{dE}{kT})$ $k$为某一常数。

由于是退火过程，所以$dE<0$，这个公式说明了温度越高出现一次能量差为dE的降温概率就越大，温度越低，出现降温的概率就越小，由于dE总是小于0，所以$P(dE)$取值在0到1之间。AC_dreamers的伪码如下：

例题

1.（点\线）费马点：

POJ2420
给n个点，找出一个点，使这个点到其他所有点的距离之和最小，也就是求费马点，输出距离和（保留整数）。
首先随便找一个点作为初始位置，因为距离和一定是越来越小的，不可能出现先变大后变小的情况（二维平面），故我们只用考虑不断地找到最优解，于是我们用初温作为移动速度，不断地向四个方向找最小值，后来随着温度降低，移动越来越慢，直到精确值。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
using namespace std;

#define MAXN 1000
#define MAXM
#define INF 0x3f3f3f3f
typedef long long int LL;

template<class T>
void Read(T &x){
    x=0;char c=getchar();bool flag=0;
    while(c<'0'||'9'<c){if(c=='-')flag=1;c=getchar();}
    while('0'<=c&&c<='9'){x=x*10+c-'0';c=getchar();}
    if(flag)x=-x;
}

const int dx[4]={0,1,0,-1};
const int dy[4]={1,0,-1,0};
struct Point{int x,y;};
double dist(const Point &a,const Point &b){return sqrt((double)(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
double getsum(Point pos,Point *p,int n){
    double ret=0;
    for(int i=1;i<=n;++i)
        ret+=dist(pos,p[i]);
    return ret;
}

const double T = 100;
const double Tmin = 1e-1;
const double delta = 0.98;
double MoNi(Point *p,int n){
    Point now=p[1],newed;
    double t=T;
    double ans=INF;
    while(t>Tmin){
        bool flag=true;
        while(flag){
            flag=false;
            for(int i=0;i<4;++i){
                newed.x=now.x+t*dx[i];
                newed.y=now.y+t*dy[i];
                double tp=getsum(newed,p,n);
                if(ans>tp)now=newed,ans=tp,flag=true;
            }
        }
        t*=delta;
    }

    return ans;
}

Point A[MAXN+10];
int n;

int main(){
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i)Read(A[i].x),Read(A[i].y);
        printf("%0.0lf\n",MoNi(A,n));
    }
}

给n条线段，找出一个点，使这个点到所有线段的距离之和最小，输出距离和（保留整数）。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
#include<cstdlib>
using namespace std;

#define MAXN 1000
#define MAXM
#define INF 0x3f3f3f3f
typedef long long int LL;

const double EPS = 1e-5;
int Sign(const double x){
    if(x>EPS)return 1;
    else if(x<-EPS)return -1;
    else return 0;
}

struct Point{
    double x,y;
    Point(){}
    bool Read(){return (~scanf("%lf%lf",&x,&y)?1:0);}
    Point(double a,double b):x(a),y(b){}
    Point operator + (const Point &a)const{return Point(x+a.x,y+a.y);}
    Point operator - (const Point &a)const{return Point(x-a.x,y-a.y);}
    Point operator * (const double a)const{return Point(x*a,y*a);}
    Point operator / (const double a)const{return Point(x/a,y/a);}
    double operator * (const Point &a)const{return x*a.x+y*a.y;}
    double operator ^ (const Point &a)const{return x*a.y-y*a.x;}
    double Lenth()const{return sqrt(x*x+y*y);}
    Point Unit()const{return (*this)/Lenth();}
};

struct Line{
    Point a,b;
    Line(){}
    bool Read(){return a.Read()&&b.Read();}
    Line(Point _a,Point _b):a(_a),b(_b){}
    Point GetPoint()const{return b-a;}
};

double Cross(const Point &a,const Point &b){return a^b;}
double Dist(const Point &a,const Point &b){return (b-a).Lenth();}
double Dist(const Line &l,const Point &p){
    if(Sign(l.GetPoint().Lenth())==0)return Dist(l.a,p);
    else if(Sign((l.b-l.a)*(p-l.a))<=0)return Dist(l.a,p);
    else if(Sign((l.a-l.b)*(p-l.b))<=0)return Dist(l.b,p);
    else return fabs(Cross(l.b-l.a,p-l.a))/l.GetPoint().Lenth();
}

double GetSum(Line *l,int n,Point pos){
    double ret=0;
    for(int i=1;i<=n;++i)
        ret+=Dist(l[i],pos);
    return ret;
}

const int dx[4]={0,1,0,-1};
const int dy[4]={1,0,-1,0};
const double T = 100;
const double Tmin = 1e-3;
const double delta = 0.98;

double MoNi(Line *l,int n){
    Point now=l[1].a,newed;
    double t=T;
    double ans=INF;
    while(Sign(t-Tmin)>0){
        bool flag=true;
        while(flag){
            flag=false;
            for(int i=0;i<4;++i){
                newed=Point(now.x+t*dx[i],now.y+t*dy[i]);
                double tp=GetSum(l,n,newed);
                if(Sign(ans-tp)>0)ans=tp,now=newed,flag=true;
            }
        }
        t*=delta;
    }
    return ans;
}

Line l[MAXN+10];
int n;

int main(){
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;++i)l[i].a.Read(),l[i].b=l[i].a;
        printf("%0.0lf\n",MoNi(l,n));
    }
}

2.最小包含球

POJ2069
给出三维平面上n个点，求用一个最小半径的球将所有点包含，输出半径（精确到5位小数）
我们可以知道，四个点确定一个球，那么我们的最小半径球上也应刚好有小于等于个点，即对于当前球心我们应向离其最远的那个点的方向按温度T移动。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<queue>
#include<stack>
#include<vector>
using namespace std;

#define MAXN 30
#define MAXM
#define INF 0x3f3f3f3f
typedef long long int LL;

struct Point{
    double x,y,z;
    void Read(){scanf("%lf%lf%lf",&x,&y,&z);}
};

double Dist(Point a,Point b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)+(a.z-b.z)*(a.z-b.z));
}

double GetR(Point *p,int n,Point pos){
    double ret=0;
    for(int i=1;i<=n;++i)
        ret=max(ret,Dist(p[i],pos));
    return ret;
}

const double EPS = 1e-7;
int Sign(const double x){
    if(x>EPS)return 1;
    else if(x<-EPS)return -1;
    else return 0;
}

const int dx[6]={-1,1,0,0,0,0};
const int dy[6]={0,0,-1,1,0,0};
const int dz[6]={0,0,0,0,-1,1};

const double T = 10;
const double Tmin = 1e-6;
const double delta = 0.98;

double MoNi(Point *p,int n){
    Point now=p[1];
    double t=T;
    double ans=INF;
    while(Sign(t-Tmin)>0){
        int k=1;
        for(int i=1;i<=n;i++)
            if(Dist(now,p[i])>Dist(now,p[k]))k=i;
        double d=Dist(now,p[k]);
        ans=min(ans,d);
        now.x+=(p[k].x-now.x)/d*t;
        now.y+=(p[k].y-now.y)/d*t;
        now.z+=(p[k].z-now.z)/d*t;
        t*=delta;
    }
    return ans;
}

Point p[MAXN+10];
int n;

int main(){
    while(~scanf("%d",&n)&&n){
        for(int i=1;i<=n;++i)p[i].Read();
        printf("%0.5lf\n",MoNi(p,n));
    }
}

4.函数最值

HDU2899
给出方程$f(x)=6\times x^7+8\times x^6+7\times x^3+5\times x^2-y\times x (0\leq x\leq 100)$
求其在取值范围上的最小值。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
using namespace std;

#define MAXN
#define MAXM
#define INF 0x3f3f3f3f
typedef long long int LL;

const double EPS = 1e-6;
int Sign(const double x){
    if(x>EPS)return 1;
    else if(x<-EPS)return -1;
    else return 0;
}

const int ITER = 10;
const double T = 100;
const double Tmin = 1e-5;
const double delta = 0.98;

double Random(){
    double x=rand()*1.0/RAND_MAX;
    if(rand()&1)x*=-1;
    return x;
}

double x[ITER+5];
double F(double x,double y){
    return 6*x*x*x*x*x*x*x+8*x*x*x*x*x*x+7*x*x*x+5*x*x-y*x;
}

void Init(){
    for(int i=0;i<ITER;++i)
        x[i]=fabs(Random())*100;
}

double MoNi(double y){
    double t=T;
    while(Sign(t-Tmin)>0){
        for(int i=0;i<ITER;++i){
            double tmp=F(x[i],y);
            for(int j=0;j<ITER;++j){
                double _x=x[i]+Random()*t;
                if(Sign(_x)>=0&&Sign(_x-100)<=0){
                    double tp=F(_x,y);
                    if(tmp>tp)tmp=tp,x[i]=_x;
                }
            }
        }
        t*=delta;
    }

    double ret=INF;
    for(int i=0;i<ITER;++i)
        ret=min(ret,F(x[i],y));
    return ret;
}

int main(){
    int T;
    double y;

    scanf("%d",&T);
    while(T--){
        scanf("%lf",&y);
        Init();
        printf("%0.4lf\n",MoNi(y));
    }
}

5.物理中力的平衡问题

BZOJ3680
给定n个点的位置和拉力大小，求最后与n个点通过细线相连的点会静止在哪里（可以看做当力平衡时动能突然损耗为0），忽略摩擦力及所有除n个点拉力以外的所有外力。
暴力模拟退火，温度调整精度，向着合外力方向移动。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<stack>
#include<vector>
using namespace std;

#define MAXN 10000
#define MAXM
#define INF 0x3f3f3f3f
typedef long long int LL;

const double EPS = 1e-4;
int Sign(const double x){
    if(x>EPS)return 1;
    else if(x<-EPS)return -1;
    else return 0;
}

struct Point{
    double x,y;
    Point(){}
    Point(double a,double b):x(a),y(b){}
    void Read(){scanf("%lf%lf",&x,&y);}
    void print(){printf("%0.3lf %0.3lf",x,y);}
    bool operator == (const Point &a)const{return Sign(x-a.x)==0&&Sign(y-a.y)==0;}
    bool operator != (const Point &a)const{return !((*this)==a);}
    Point operator + (const Point &a)const{return Point(x+a.x,y+a.y);}
    Point operator - (const Point &a)const{return Point(x-a.x,y-a.y);}
    Point operator * (const double a)const{return Point(x*a,y*a);}
    Point operator / (const double a)const{return Point(x/a,y/a);}
    Point operator += (const Point &a){return (*this)=(*this)+a;}
    double Lenth()const{return sqrt(x*x+y*y);}
    Point Unit()const{return (*this)/Lenth();}
};

Point pos[MAXN+10];
double F[MAXN+10];
int n;

Point GetSum(const Point &now){
    Point ret=Point(0,0);
    for(int i=1;i<=n;++i)
        if(pos[i]!=now)ret+=(pos[i]-now).Unit()*F[i];
    return ret;
}

const double T = 20000;
const double Tmin = 1e-5;
const double delta = 0.99;

Point MoNi(){
    Point now=pos[1],newed;
    double t=T;
    while(Sign(t-Tmin)>0){
        now+=GetSum(now).Unit()*t;
        t*=delta;
    }

    return now;
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i)pos[i].Read(),scanf("%lf",&F[i]);
    MoNi().print();
}

6.旅行商问题

在模拟退火前，我只会$2^n$，现在可以用模拟退火来求近似值了。。。。。。只是近似值（哭）
模拟退火的TSP求法更多的是生成随机排列当做粒子，然后乱搞搞。
调了半天参数，就只能到72%。

结果我一把我的随机种子从我的生日换成hcx的生日，然后…

之后我又硬怼了40分钟，终于终于A了!!!!!

下附源码。主要看参数。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
using namespace std;

#define MAXN 20
#define MAXM
#define INF 0x3f3f3f3f
typedef long long int LL;

template<class T>
void Read(T &x){
    x=0;char c=getchar();bool flag=0;
    while(c<'0'||'9'<c){if(c=='-')flag=1;c=getchar();}
    while('0'<=c&&c<='9'){x=x*10+c-'0';c=getchar();}
    if(flag)x=-x;
}

int G[MAXN+5][MAXN+5];
int n;

struct Path{
    int way[MAXN+5];
    int len;
};

const double EPS = 1e-5;
int Sign(const double x){
    if(x>EPS)return 1;
    else if(x<-EPS)return -1;
    else return 0;
}

double Random(){
    return rand()*1.0/(RAND_MAX+1.0);
}
double Random(int l,int r){
    return l+rand()%(r-l+1);
}

const int ITER = 2000;      //粒子数量
const double T = 10000;     //初始温度
const double Tmin = 1e-3;   //温度下限（阀值）
const double delta = 0.98;  //温度下降速度
const double oloop = 200;   //外部温度限制循环次数
const double iloop = 10000; //在统一温度下的循环次数
const double LIMIT = 800;   //容错能力（次数）

Path GetNxt(const Path &now){
    Path newed=now;
    int a=(int)n*Random();
    int b=(int)n*Random();
    while(!G[a][b])a=(int)n*Random(),b=(int)n*Random();
    swap(newed.way[a],newed.way[b]);
    newed.len=0;
    for(int i=0;i<n-1;++i)newed.len+=G[newed.way[i]][newed.way[i+1]];
    return newed;
}

Path now[ITER+5];
int pl[MAXN+5];
void Init(){
    for(int i=0;i<n;++i)pl[i]=i;
    for(int i=1;i<=ITER;++i){
        for(int j=0;j<n-1;++j){
            int a=Random(j,n-1);
            swap(pl[j],pl[a]);
        }
        now[i].len=0;
        for(int j=0;j<n;++j)now[i].way[j]=pl[j];
        for(int j=0;j<n-1;++j)now[i].len+=G[pl[j]][pl[j+1]];
    }
}

int MoNi(){
    Path newed,ret;
    ret=now[1];
    for(int i=2;i<=ITER;++i)
        if(now[i].len<ret.len)ret=now[i];

    int P_L[ITER+5],P_F=0;
    memset(P_L,0,sizeof(P_L));

    double t=T;
    while(1){
        for(int i=1;i<=ITER;++i){
            for(int j=0;j<iloop;++j){
                newed=GetNxt(now[i]);
                double dE=newed.len-now[i].len;
                if(dE<0)now[i]=newed,P_L[i]=P_F=0;
                else{
                    if(Sign(exp(dE/t)-Random())>0&&Sign(exp(dE/t)-1)<0)
                        now[i]=newed;
                    P_L[i]++;
                }

                if(P_L[i]>LIMIT){
                    ++P_F;
                    break;
                }
            }

            if(ret.len>now[i].len)
                ret=now[i];
        }
        if(P_F>oloop||Sign(t-Tmin)<=0)
            break;
        t*=delta;
    }

    return ret.len;
}

int main(){
    srand(20010627);        //还有种子，最重要最重要最重要！！！

    Read(n);
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j)Read(G[i][j]);
    Init();
    printf("%d\n",MoNi());
}
/*
4
0 1 2 3
2 0 1 3
1 2 0 3
3 3 3 0
*/