Brodal queue简要说明-CSDN博客

本文链接：https://blog.csdn.net/qq_35571432/article/details/105440479

Brodal queue简要说明

前言

Brodal queue（没找到国内的比较通用的翻译）是目前为止复杂度最好的堆。其具体的操作复杂度为:

操作	复杂度
find_min	O(1)
delete_min	O(log n)
insert	Θ(1)
decrease-key	Θ(1)
meld	Θ(1)

它是第一个不用摊销操作就能实现这些复杂度的堆^[1]。

尽管他复杂度低，但是工业中运用比较少，因为其实现复杂，而且存在大量的双链表操作，导致其复杂度对应的常数相当高。^[2]

Brodal队列在Brodal的论文中被最先提出，论文的链接为：https://www.cs.au.dk/~gerth/papers/soda96.pdf

另外推荐某404网站上关于Brodal Queue的介绍，链接为https://www.quora.com/How-do-Brodal-queues-work^[3]，这个相对论文来说更好读一点，但是也缺少了非常多的细节。

这里介绍的是用来快速寻找最小值的Brodal Queue，需要寻找最大值反过来即可。

数据结构

首先需要知道几点：

一些基本概念。
p(x)：x的父节点。
r(x)：x的秩(rank),也可以理解为树高度。
t_i：T_i树的根。
每个队列包含两个树，T1和T2。
节点的子节点按从右到左递增的顺序存储在双链表中，同时还有指向最左边子节点和父节点的指针（也就是4个指针）。
Violating nodes，指那些不符合父节点小于子节点这一标准的节点。
每个节点如果有孩子是rank j的（秩为j），那么节点rank为j的孩子有2-7个（最小为2，最大为7）。
W(x)和V(x)。W(x)和V(x)分别存T1和T2中比x这一节点值大的节点。其用双链表存储。具体来说，W(x)存的是rank比x小的节点，V(x)则是剩下的。向V中添加节点一直添加在在V列表最前面，而向W列表添加时rank相近的节点添加在一起。
Violation list。其存储了Violating nodes。

guides

和斐波那契堆类似，Brodal也是采用类似二进制计算的形式。Brodal采用的是一种叫Guides的数据结构，其目标具体来说是为了保证：根至少有每种rank子节点两个；w数组中子节点每种的rank的数量不超过6。

其使用情景如下：
需要维护一个x₁₆到x₁的队列，条件是x_i小于等于T(T是一个阈值，threshold，不是前面说的树)。这里我们假设T=2,假如我们需要做一个加很多2的操作，但是我们只允许对结果操作O(1)次。Guide就是来找到需要做什么操作的。

在前面提到过，guide的作用有两种，这里假设其已经发挥了作用，使得根节点有着各种rank的子节点2-7个，为了让guide更好的计算出我们需要进行的操作（这里T=2，意味着我们进行两种操作，加和减），我们新开一个x^’_i并对其做如下操作：
对于进行加操作的guide，把数量为2-5的都设置为0，6设置为1，7设置为2。
对于进行减操作的guide，把数量为7-4的都设置为0，3设置为1，2设置为2。
对于加操作来说，是减2和加1，对于减操作来说，是加2和减1。

但是guide还需要对应回节点，这里还需要另外开一个数组，用来指向对应的内存单元。内存单元指向的是最左边的元素的索引或者值（这意味着同一个块的元素指向相同的内存单元）。这里这个块我还没完全理解，但是参考论文中提到的连续的块，似乎是内存分配单位？这样做有两个好处：给一个元素我们可以快速找到其在内存块中最左边的元素(O(1));在O(1)时间内删除块。如图是一个例子，下划线表示相同的块。
avator
下图是一个作为例子的Guide的数据结构(出自论文)
avator

操作

链接和断开

当我们需要把具有相同rank的x1，x2，x3合并，并且这三者没有根节点，那么找到最小的然后把其他两个作为其最左边节点即可，不会出现Violating node。并且仍然满足准则S和O这十条。

当我们需要把根节点x的儿子移走时，当其具有2-3个rank为rank(x)-1孩子时，如果把这2-3个孩子都移走，这时候x的rank是其孩子最大rank+1，如果当其具有4个及以上rank为rank(x)-1的孩子时，可以轻松的移除两个。

总体来说，移除一棵rank k的子树，总是会导致2-3个k-1的树和一个额外的rank最大为k的树。如图所示：
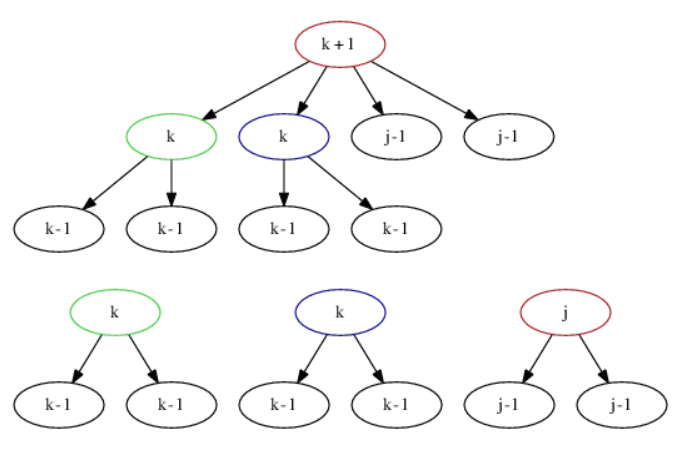
avator

维护根节点的孩子

对于根节点，添加或者删除子节点需要维护准则R1，这时候需要使用4个guide，T1和T2各两个，这里仅以T1为例，T2类似。

为了保证对于t1的孩子节点的访问时间能控制在常数时间内，这里我们需要维护一个变长数组来指向t1的rank为0到r(t1)-1的孩子节点。R1准则规定了其必须存在。Guide主要针对rank 小于等于r(t1) - 3的孩子节点，对于其他两种rank独立处理（直接处理保证其在2-7范围内），这样做是为了避免由于两个guide之间相对独立（一个guide负责上边界，一个guide负责下边界）导致的问题。

当我们向t1中添加rank为i节点的时候（i < r(t1) - 2)，guide会告诉我们在哪里操作。当这个操作导致树高度增长时，我们也要扩充相应的guide域。

对于t1，由于其根节点是最小值，因此我们的操作不会引起Violating node，但是对于t2，删除操作是会引起三个Violatings。因此我们仅删除t2中rank大于r(t1)的节点。当删除后剩余的tree的rank小于r(t1)时，将其作为t1的孩子，否则作为t2的，产生的Violating Node根据其rank放置在V中。

冲突减少转换(Violation reducing transformations)

这里的冲突减少针对y，y属于T1和T2交集，有V(y)和W(y)。

假设我们现在有两个冲突节点，x1和x2，并且x1和x2具有相同的rank（这里已经确保这两个节点都是Violating node）。假如x1和x2不是兄弟（这里我们假设x1的父节点更小），那样我们把x2换过来做x1的兄弟。如果x1有不少于一个兄弟，那么把x1切下来作为t1的子节点。假如x1和x2已经是兄弟了，并且是仅有的两个孩子节点，这时候如果r(y)>r(x1)+1,直接将x1和x2切下来作为t1的子节点。但是如果r(y)=r(x1)+1,这个时候我们将x1,x2,y全部切下来，y的rank将由他新的最左边的儿子决定（+1），然后用t1的同rank的子节点替换y。这时，如果y是t1的子节点，那么我们只切下y。如果替换y的节点是Violating node，那么我们把这个节点加入到W(t1)。

避免过多Violating node

这里主要介绍下减少Violating node的方法。

首先，我们只往V(t1)和W(t1)添加Violating node。然后W(t1)的内容被guide监视，guide保证W(t1)的节点数少于6（规则O4）。当加入节点后W(t1)的节点数超过6个时，会进行冲突减少转换操作（在guide指导下）。

当我们对queue执行操作的时候，通过将T2的子树移到T1来将t1的rank提高至少1，可以减少alpha个Violating node(rank 大于r(t1))(规则O5)，

常用的操作

Insert 插入

作为meld的一种特例。

Meld 合并(Q1和Q2)

合并涉及四棵树（每个队列两棵），拥有最小的根节点的树是新的T1（由于O1准则，这棵树应该是Q1或者Q2的T1树），如果这棵树拥有最大的rank，我们仅需把其他几棵树加进去。这是最简单的情况。

否则拥有最大rank的这棵树成为新的T2树，这时候把剩下的树加进去，如果某一棵树的rank和新T2树相等，还需要进行拆分。

Decrease Key

用新的值代替旧的。如果新的值小于t1，我们把t1和新的值做一个交换。如果新的值是好节点我们停止（即满足父节点小于任意子节点），否则做减少Violating node处理。

Delete MIN 删除最小值节点

这个是操作中最复杂的，复杂度达到了O(log n)。首先通过把T2的孩子移到T1树来把T2树清空，这时候T2树的根节点作为T1树的根节点的一个rank 0的子节点。然后删除t1。这时候有O(log n)棵非独立子树。然后在V和W集中以及子树的根节点中寻找最小值。如果这个最小值不是根，那么我们把他和一个rank相同的非独立子树的根交换，然后将新的节点最为最小值节点，将非独立子树们作为新的节点的孩子，然后进行O(log n)次链接和断开操作，就可以让新的树遵守准则S1-S5，R1和R3。然后将现在根节点的V和W集合并，然后将旧的V和W集并入，这一步的开销也是O(log n)，然后做冲突减少转换（最多O(log n)次)来使得每个rank最多有一个Violating node，然后将现在的作为新的W集，把V集置空，使得满足O1-O5以及R2准则。

删除某一节点

先将待删除节点使用Decrease Key，并将新的key设置为负无穷，然后使用删除最小值节点方法。

优先队列操作

准则

S1：叶子的rank为0
S2：节点的rank小于其父节点
S3：rank为j的节点（j>0），至少有两个rank为j-1的子节点
S4：rank为x的节点还有rank为j的子节点节点的数量为0，2-7
S5：T2为空或者t1的秩小于t2

O1：t1是T1和T2里面的最小值
O2：如果y在V(x)和W(x)中，y>x
O3：如果y小于其父节点，那么应该存在一个不等于y的x使得y属于V(x)或者W(x)
O4：w_i(x) < 6
O5：if V(x) = (y_|V(x)|,…,y2,y1),then r(y_i) >= (i-1)/alpha 向下取整，其中i=1,2,…,|V(x)|,alpha为常数

R1：t_j含有的rank为j的子节点的个数为2-7
R2：|V(t_i) <= alpha * r(t1),alpha是常数
R3：如果y在W(t1)里面，那么r(y) < r(t1)