GEE：对NDVI的时间序列使用Sen+Mann-Kendall（MK）趋势检验

---

Sen+MK趋势分析

Sen 斜率估计用于计算趋势值，通常与MK非参数检验结合使用。即首先计算Sen趋势值，然后使用MK方法判断趋势显著性。
本文使用非参数 Mann-Kendall 检验检测图像中是否存在递增或递减趋势和 Sen 斜率以量化趋势的大小（如果存在）来检测图像中的单调趋势。
本文还展示了估计 Mann-Kendall 检验统计量的方差、用于检验是否存在任何趋势的 Z 统计量以及统计量的 P 值（假设为正态分布）。
需要注意的是，这里介绍的方法适用于评估离散数据（即非浮点数）中的单调趋势（即没有季节性的数据）。

算法详解博客1：https://www.jianshu.com/p/eae362946ea9
算法详解博客2：https://zhuanlan.zhihu.com/p/112703276

GEE源代码链接：https://code.earthengine.google.com/1149eef0974687085727c02e58152d6b?noload=true
参考资源：https://developers.google.com/earth-engine/tutorials/community/nonparametric-trends

---

结果展示

MK趋势 检验结果如下图所示：

斜率 结果如图所示：

截距 结果如下图所示：

---

Sen_slope

Sen_slope： Theil-Sen Median方法又被称为Sen 斜率估计，是一种稳健的非参数统计的趋势计算方法。该方法计算效率高，对于测量误差和离群数据不敏感，常被用于长时间序列数据的趋势分析中。

式中: xi和xj为时间序列数据。β大于0表示时间序列呈现上升趋势; β小于0表示时间序列呈现下降趋势。

Mann-Kendall是一种非参数统计检验方法，最初由Mann在1945年提出，后由Kendall和Sneyers进一步完善，其优点是不需要测量值服从正态分布，也不要求趋势是线性的，并且不受缺失值和异常值的影响，在长时间序列数据的趋势显著检验中得到了十分广泛的应用。其统计检验方法如下:

对于时间序列Xi，i=1, 2, …i, …j, …n。定义标准化检验统计量Z:

式中：xi和xj为时间序列数据，n为数据个数；当n≥8时，检验统计量S近似为正态分布，其均值和方差如下：在给定显著性水平α下，如果$$|Z|>Z_{1-\frac{\alpha }{2}}$$则表明不存在趋势的假设被拒绝，时间序列数据存在明显的趋势变化。$$Z_{1-\frac{\alpha }{2}}$$为在置信水平α下，标准正态函数分布表对应的值。当Z的绝对值大于1.65、1 .96和2.58时，表示趋势分别通过了信度为90%、95%和99%的显著性检验。

Z值

z值 如图所示：

---

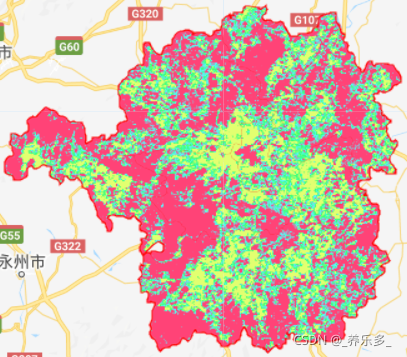
应用案例

此图来自论文（Establishing forest resilience indicators in the hilly red soil region of southern China from vegetation greenness and landscape metrics using dense Landsat time series）
绿线是NDVI的时间序列曲线，可以看出NDVI是增加趋势，并且显著性大于1.96。（其他颜色的序列是其他指标，和本文关系不大）

d图表示NDVI比较稳定。