第二次模拟赛题目讲解

1

C
本题考察的是进制相关的知识，在计算机中，我们常用的有2进制，8进制，10进制，16进制。
本题我们将四个数都转化为十进制比较。
A 转化为十进制为$555$
B转化为十进制是$7\ast 8\ast 8+7\ast 8+7=511$
C转化为十进制是$1024$
D转化为十进制是$2\ast 16\ast 16+2\ast 16+15=559$

2

B
数据结构栈，先进后出，后进先出
每次操作后栈内元素为
a
a,b
a
a,c
a,c,d
a,c
因此栈底元素是a

3

C
插入排序稳定 O（N^2）
冒泡排序一般是O（N^2）的，极端数据能到O（N）
归并排序稳定O（NlogN）
快速排序随机数据O（NlogN），极端数据会退化到O（N^2)

4

C
共有5层。每层有1，3，9，27，81个结点，所以第一个结点的第1个孩子的编号是2，第2个是42（因为总共有5层，第1个下面有4层，共40个孩子），第3个是82。结点82的第一个孩子有13个结点，第二个孩子的编号是96，此时距离100非常近，所以直接往下衍生，不难发现，96的第一个孩子是97，97的第三个孩子是100，所以100的父亲是97，选C

5

C
字母有26个，阿拉伯数字有10个，所以答案是2626101010=676000

6

B
一道递归问题，一步步分析就好了，可以在纸上写出递归过程，并且复用一些计算结果。
ack(2,2)=
ack(1,ack(2,1))=
ack(1,ack(1,ack(2,0)))=
ack(1,ack(1,ack(1,1)))=
ack(1,ack(1,ack(0,ack(1,0))))=
ack(1,ack(1,ack(0,ack(0,1))))=
ack(1,ack(1,ack(0,2)))=
ack(1,ack(1,3))=
ack(1,ack(0,ack(1,2)))=
ack(1,ack(0,ack(0,ack(1,1))))=
ack(1,ack(0,ack(0,ack(0,ack(1,0)))))=
ack(1,ack(0,ack(0,ack(0,ack(0,1)))))=
ack(1,ack(0,ack(0,ack(0,2))))=
ack(1,ack(0,ack(0,3)))=
ack(1,ack(0,4))=
ack(1,5)=
ack(0,ack(1,4))=
ack(0,ack(0,ack(1,3)))=
ack(0,ack(0,5))=
ack(0,6)=
7

7

C
快速排序的原理是找到一个基准，并且把比基准小的数放在基准左侧，比基准大的数放在右侧。
对于已经有序的序列，每次都选择最左侧的值作为基准，每次需要扫描长度次，并且下次递归的长度为n-1
因此总的次数的是1+2+3+n次，根据等差数列可知，这个和是n^2级别的，因此选C。

8

C
拓扑排序的要求是图内不存在环，在本图内5，6，1三个点构成了一个环，因此只需要破坏掉这个环的一条边，让图内不存在环就可以进行拓扑排序了。

9

A
本题可以设$n=2^i$
那么可以分层级来看这个问题
参数为$n=2^i$的quick_power 有$2^0个$
参数为$n=2^{(}i-1)$的quick_power 有$2^1个$
参数为$n=2^{(}i-2)$的quick_power 有$2^2个$
…
参数为$n=2^0$的quick_power 有$2^i个$
总和为$2^0+2^1+...+2^i=2\ast n$因此是O(n)级别的。

10

C
在图论中，一棵树的重心指的是去除掉这个重心后，剩余的联通块内，最大的块内点的数量最少。
结论：一颗树最多只有两个重心且相邻，并且奇数个点的树不存在多个中重心，偶数个点的树可能存在多个重心。

11

B
本题考察的是最短路径问题，我们可以模拟迪杰斯特拉算法来寻找单源最短路。
dis = [0，2，5，1，INF，INF，INF，INF，INF]
dis = [0，2，5，1，14，13，12，INF，INF，INF]
dis = [0，2，5，1，14，13，12，INF，INF，INF]
dis = [0，2，5，1，11，13，9，INF，INF，INF]
dis = [0，2，5，1，11，13，9，17，19，INF]
dis = [0，2，5，1，11，13，9，16，19，INF]
dis = [0，2，5，1，11，13，9，14，19，INF]
dis = [0，2，5，1，11，13，9，14，19，INF]
dis = [0，2，5，1，11，13，9，14，19，19]

12

D

	A
   / \
  C   B
 /     \
D       I
 \
  E
   \
    F
   /
  G
   \
    H

13

A
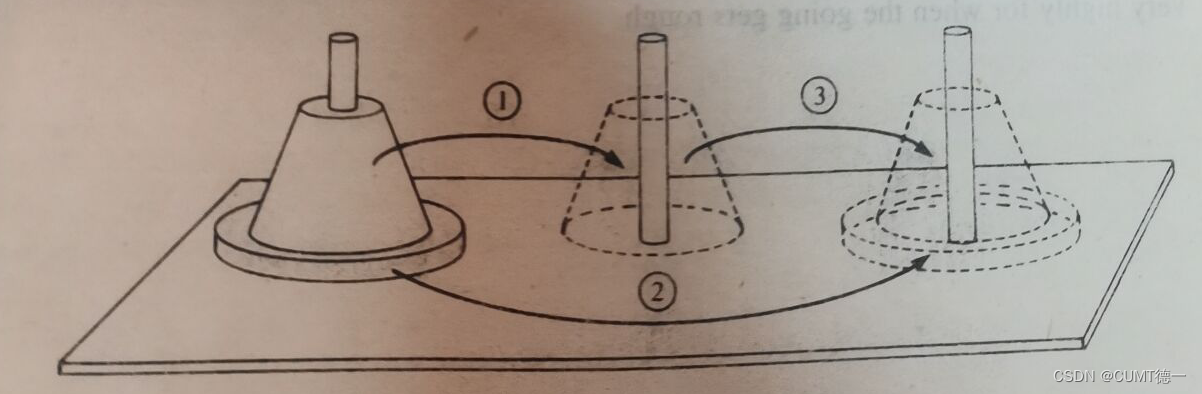
算法采用了分治的思想，利用递归的方式，完成n层汉诺塔的移动。
当n=1时，只要将编号为1的圆盘从柱子A直接移到柱子C上即可。

当n>1时，就需要借助另外一根柱子来移动。将n个圆盘由A移到C上可以分解为以下几个步骤：

(1)  将A柱子上的n-1个圆盘借助C柱子移到B柱子上;

(2)  把A柱子上剩下的一个圆盘从A柱子移到C柱子上;

(3)  最后将剩下的n-1个圆盘借助A柱子从B柱子移到C柱子上。

假定n是圆盘的数量，T(n)是移动n个圆盘的移动次数。
当n=1时，T(1)=1
当n=2时，T(2)=2T(1)+1
当n=3时，T(3)=2T(2)+1

14

C
有 8 个苹果从左到右排成一排，要求从中选出至少一个，并且不能选择相邻的两个苹果，一共有多少种选法？

这是一个经典的排列组合问题，满足如下条件：
从 n 个物品中选择若干个；
不能选择相邻的两个；
至少选择一个。
设 f(n) 表示从 n 个苹果中选择若干个（可以为 0 个），且不选相邻苹果的方案数。
我们有如下递推关系：
f(n) = f(n - 1) + f(n - 2)
解释：
不选第 n 个苹果：相当于从前 n - 1 个苹果中选，方案数是 f(n - 1)；
选第 n 个苹果：第 n - 1 个不能选，只能从前 n - 2 个中选，方案数是 f(n - 2)。
f(0) = 1 （全不选）
f(1) = 2 （选或不选第一个）

f(2) = f(1) + f(0) = 2 + 1 = 3
f(3) = f(2) + f(1) = 3 + 2 = 5
f(4) = 5 + 3 = 8
f(5) = 8 + 5 = 13
f(6) = 13 + 8 = 21
f(7) = 21 + 13 = 34
f(8) = 34 + 21 = 55

f(8) = 55 包含了“不选任何一个苹果”的方案。题目要求至少选一个苹果，因此需要减去这种情况：

最终答案 = f(8) - 1 = 55 - 1 = 54

15

A

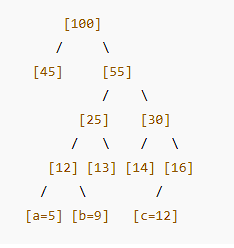
16

（1）^ 是异或号，<< 是左移，>>是右移，两个数不完全一样，必然不为0。
（2）如果改为unsigned int，则该题中的机器数都是32位机器数。
对于某些高位有1的情况，如果x是16位机器数，x<<6会溢出，再进行x>>8高8位一定为0。
而如果x是32位机器数，x<<6不会溢出，再进行x>>8高8位可能不为0。
由于一些计算过程中机器数中的1比较少，表示一个机器数可以不用写出机器数的每一位，只需要标出其有1的位置即可。比如第i位（从0开始数）有1，就可以写1<<i，第i位和第j位有1可以记为1<<i | 1<<j
例：输入的x是32768，也就是1<<15


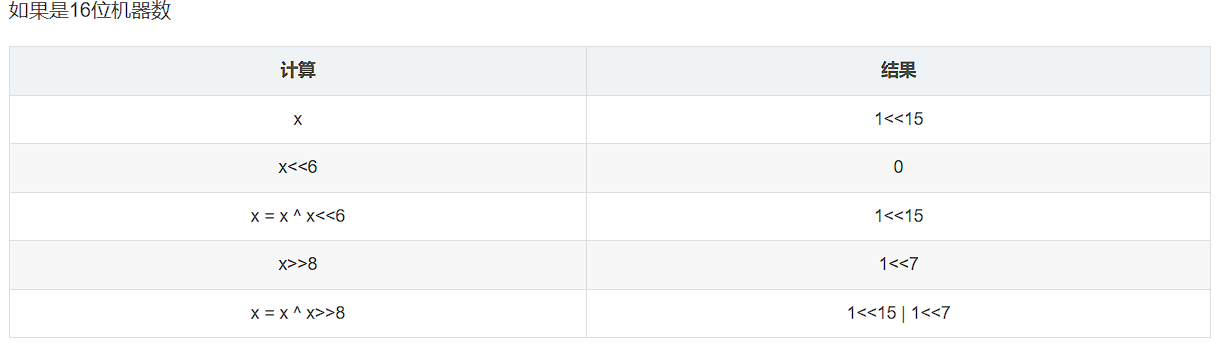
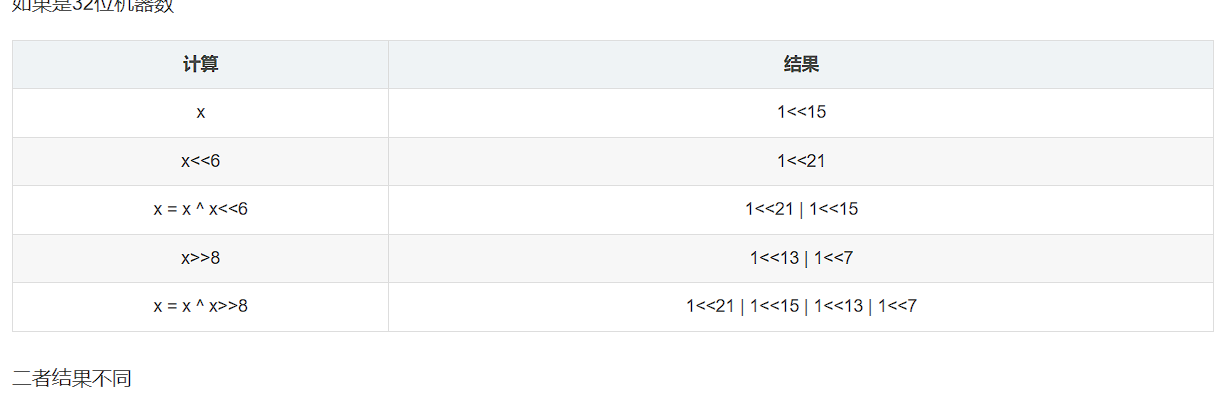
（3）

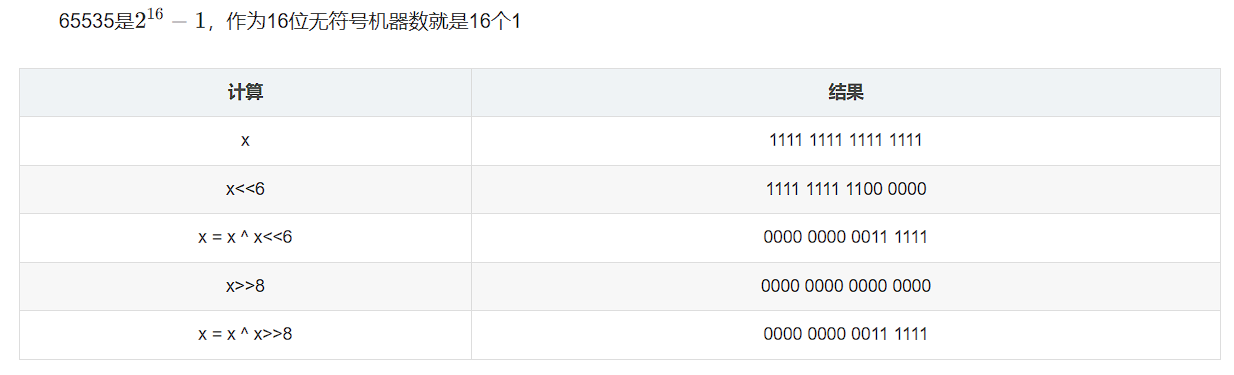
（4）

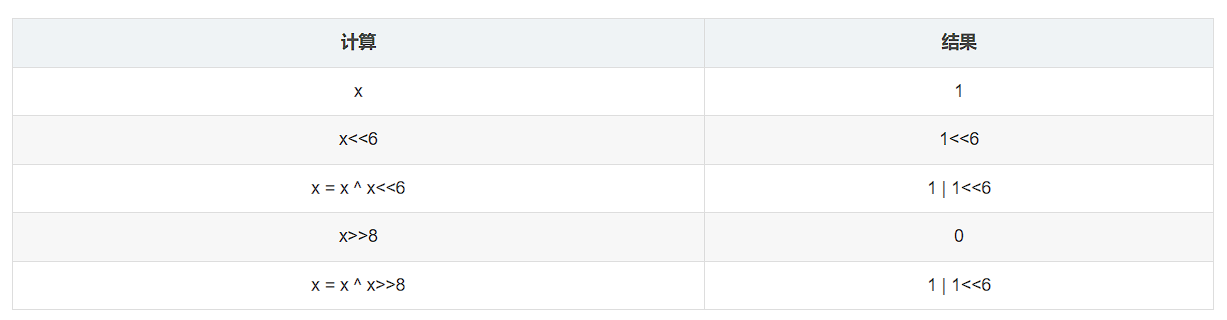
（5）

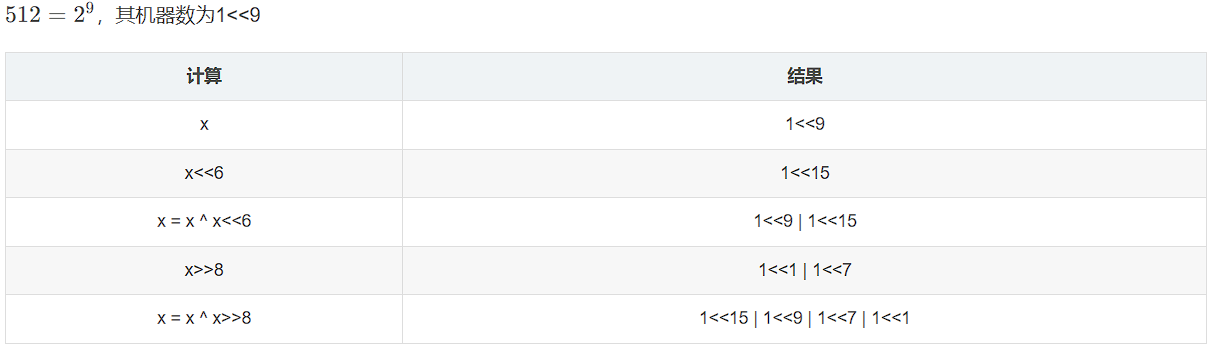
（6）

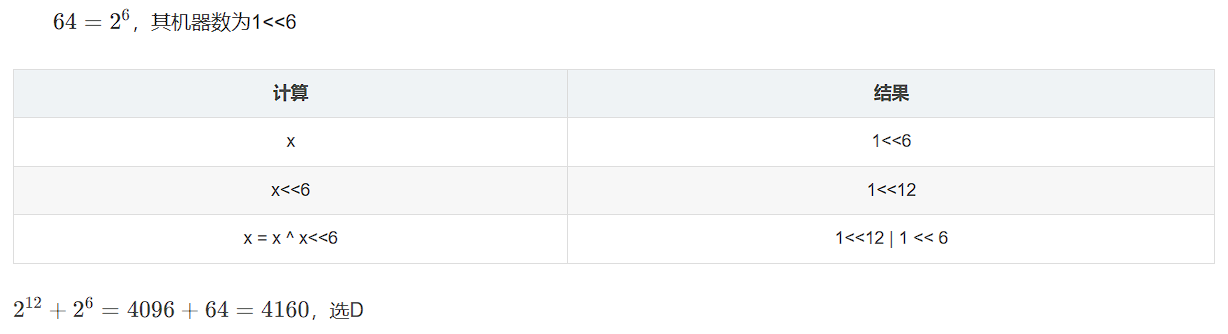
17

本题考察的是k进制下的基数排序。
（1）
所谓排序算法稳定不稳定，就是看相同值的相对次序在排序后有无变化。
基数排序是稳定的，而像堆排序，快速排序是不稳定的。
（2）
空间复杂度显示是跟值域有关系的。
（3）
看循环叠加。
（4）
第一次运行到36行，就是看三进制下的第一位大小。
98 % 3 = 2
26 % 3 = 2
91 % 3 = 1
37 % 3 = 1
46 % 3 = 1
并且排序是稳定的
那么排完之后从小到大是91 37 46 98 26
（5）
复杂度不仅与K有关，不能确定。
（6）
当K比Val[i]还大的时候，第一次排序就是看一个完全值了，因此退化为计数排序。

18

本题是一个经典的动态规划算法，从左上角走到右下角最少的代价是多少。
（1）
显然不是每一行最小值求和，而是从左上角走到右下角的最小路径。
（2）
把第四行删除，然后把b改为a其实是不变的。
（3）
按照动态规划模拟即可。结果如下
a =
1 3 6 10
6 9 13 18
15 19 24 30
28 33 39 46
最短路径：
(0,0) → (0,1) → (0,2) → (0,3) → (1,3) → (2,3) → (3,3)
（4）
复杂度显然是O(nm)
（5）
显然是动态规划算法。
（6）
继续模拟即可。
a =
[ 1 3 6 ]
[ 5 8 12 ]
[12 16 21 ]

19

本题考查的是拓扑排序。
因为最后被拓扑出的值后续的路径是少的，拓扑出序列后，然后逆序算出每个点的路径数量，那么第K条路径就可以按照字典序排序后按照路径数量算出。
（1）
这里找的是第K条路径，f[u]是这个点开始的路径数量，当K<=F[U]时候，就说明第K条在这可以取到。
（2）
拓扑排序，先放入再减，因此条件是==1。
（3）
计算路径数量，路径的数量明显是所有邻接点路径数量+1，因为K最大值是1e18，因此跟这个值取最小值防止爆类型。
（4）
此处需要依次输出路径，那么每次需要k>1的时候输出
（5）
再减去u唯一节点的路径。

20

本题考查的是深度优先搜索以及记忆化搜索。
（1）
这里模拟的是把第二杯水往第一个杯子里倒，t取一个最小值，是第一个杯子先被倒满，还是第二个杯子被倒空。
（2）
是上个题目的反过来
（3）
当第一个杯子的剩余水为c或者第二个为c的时候，结束。
（4）
同第一个
（5）
同第二个