STAT313 Chap3 Histogram 讲义解析（一）

本文原创笔记，禁止转载。有问题可私信付费找我咨询。

Histogram

这份PPT主要介绍了直方图的概念以及如何通过直方图来估计概率密度函数。
首先，直方图是一种统计工具，它通过将数据分组到不同的“箱”或“区间”（称为“bin”）中来估计变量的分布。这些箱的宽度是固定的，箱中包含的数据点数量代表了该区间内的观测值数量。
这张图展示了一个样本量为100的标准正态分布的直方图。从这个直方图中，我们可以大致看出数据分布的形状，接近于标准正态分布的钟形曲线。

这张幻灯片给出了直方图的数学定义。这里指出，我们需要一个独立同分布（i.i.d.）的样本 $X_i$ ，并将实数线划分为区间 $[b_k,b_{k+1}]$ ，其中 $b_j$ 是区间的边界。 $m_k$ 是落在 $k$ 个区间内的观测值的数量。
直方图公式：直方图 ${\hat{f}}_n(x)$ 在 $x$ 落在 $[b_k,b_{k+1})$ 时的值由下式给出：
$${\hat{f}}_n(x)=\frac{m_k}{n(b_{k+1}-b_k)}$$

这里， $m_k$ 是箱中的观测数， $n$ 是总样本数， $(b_{k+1}-b_k)$ 是箱的宽度。这个公式实际上是在计算每个箱的样本密度。
直方图的高度代表了每个区间内数据点的密度。这种方式，我们可以估计出概率密度函数，即概率在不同取值范围内的分布。尽管直方图是对实际概率密度的近似，但它提供了一个直观的视图来理解数据是如何分布的。

这张幻灯片进一步解释了直方图中“箱”（或称“区间”、“bin”）的概念以及它们对直方图的影响。

区间 $[b_k,b_{k+1}]$ 被称为“箱”，直方图的构造依赖于这些箱的选择。即使是很小的改变（如调整箱的边界），也可能显著改变直方图的外观。所以，在计算直方图时必须谨慎选择箱的大小和边界。

幻灯片还介绍了 regular bins（等宽箱）的概念，这意味着所有的箱都有相同的大小，即 $h=b_{k+1}-b_k$ 对所有的 $k$ 都是一样的。这里的 $h$ 被称为“箱宽”（binwidth）。箱宽 $h$ 的值以及 $b_0$ （即箱的起始位置）对直方图的外观有很大的影响。

当所有的箱都具有相同的宽度时，直方图的解释变得更加直观，因为每个箱的高度直接反映了其区间内的概率密度。但是，如果箱的宽度选择不当，可能会导致对数据分布的误解。例如，过宽的箱可能会隐藏数据的某些特征，而过窄的箱可能会产生过于嘈杂的直方图，其中的随机波动可能被错误地解释为数据的实际特征。因此，选择合适的箱宽是直方图分析中的一个关键步骤。

这张幻灯片展示了相同的数据样本在不同箱宽 $h$ 和不同起始位置 $b_0$ 下的直方图。这些直方图都是用相同的样本大小（ $n=100$ ）的标准正态分布数据生成的，但由于箱宽和箱的起始位置不同，它们看起来截然不同。

密度估计器 Density estimator

这张幻灯片介绍了如何将直方图作为一个非参数密度估计器，并提出了一个直方图密度估计器的定义。

直方图通常被看作是描述性工具，用于揭示数据中的某些结构。但它也可以被用作简单的非参数密度估计器。这张幻灯片提供了一个定义直方图的替代方式，将其视为一个密度估计器（density estimator）：
$${\hat{f}}_n(x)=\frac{{\hat{F}}_n(b_{k+1})-{\hat{F}}_n(b_k)}{b_{k+1}-b_k}\text{for}x\in [b_k,b_{k+1}).$$

这里， ${\hat{F}}_n$ 是经验分布函数的估计，而 ${\hat{f}}_n(x)$ 是 $x$ 在特定区间 $[b_k,b_{k+1})$ 内的概率密度估计。分子 ${\hat{F}}_n(b_{k+1})-{\hat{F}}_n(b_k)$ 表示的是在区间 $[b_k,b_{k+1})$ 内的概率，而分母 $b_{k+1}-b_k$ 是该区间的宽度。

这个公式可以看作是函数 ${\hat{F}}_n$ 在区间 $[b_k,b_{k+1})$ 上的平均变化率，这与微积分中导数的定义十分相似，其中导数是函数在某点的瞬时变化率。我们知道对于连续变量 $X$ ，它的概率密度函数 $f_X$ 可以通过求累积分布函数 $F_X$ 的导数来得到： $f_X=F_X^{\prime }$ 。

最后，幻灯片引出了一个问题：直方图作为密度 $f_X$ 的估计器有多好？并且提示我们需要做一些理论研究来回答这个问题。在统计理论中，评估估计器的好坏通常涉及偏差（bias）、方差（variance）以及均方误差（MSE）等概念。通过理论分析和实验模拟，我们可以更好地了解直方图估计器在不同情况下的性能表现。

这张幻灯片介绍了直方图的点态分析和利普希茨连续性的定义。

**点态分析(Point-wise analysis)**是指对直方图中单个点或者某个具体区间的观测与分析，而不是对整体直方图的全局观测。在这种分析中，我们关注直方图在特定点上的性质，如直方图在该点的高度，可以反映出在这一点附近值的分布密度。

幻灯片中指出，直方图的质量依赖于概率密度函数增长和下降的陡峭程度。这意味着，如果概率密度函数在某个区间内快速变化，直方图可能难以精确地捕捉这种变化，特别是当箱宽较大时。

利普希茨连续性是函数的一种性质，它限制了函数在任何两点之间的变化速度不能超过这两点间距离的某个固定倍数。这个倍数就是利普希茨常数 $L$ 。这种性质保证了函数的变化不会太过陡峭，有助于我们在进行数学建模或数据分析时，确保估计和模型的稳定性和可靠性。

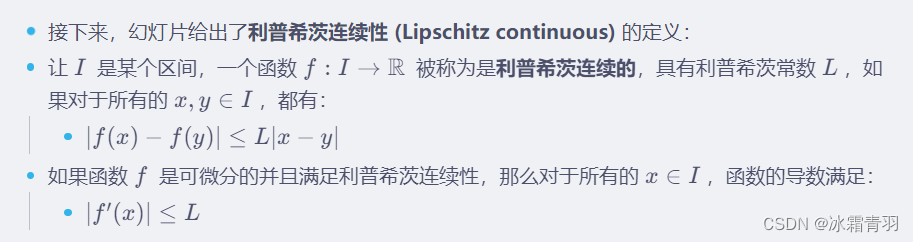
这意味着，如果函数的导数的绝对值被一个常数 $L$ 所限制，那么函数在区间 $I$ 上的变化速度就被控制了，函数不会太过陡峭。这样的性质在直方图分析中是有用的，因为如果概率密度函数是利普希茨连续的，那么直方图作为概率密度的估计器，其精确度会有一定的保障。

利普希茨常数越小，表示函数越平滑，直方图越有可能精确估计出真实的密度函数。

直方图估计的偏差（bias）

这张幻灯片在统计学的背景下探讨了直方图估计的偏差（bias）。在统计学中，偏差是指估计量的期望与被估计量真实值之间的差异。这里的关注点是直方图密度估计器 ${\hat{f}}_n(x)$ 在某固定点 $x$ 的期望与真实概率密度函数 $f_X(x)$ 之间的偏差。

让我们逐步推导这个公式：

1. 首先，我们固定一个 $x$ 并选择一个包含 $x$ 的箱 $[b_k,b_{k+1})$ ，并设定箱宽 $h=b_{k+1}-b_k$

2. 直方图估计器 ${\hat{f}}_n(x)$ 的期望偏差被定义为 $\left|E[{\hat{f}}_n(x)]-f_X(x)\right|$ 。

3. 利用概率密度函数的性质，期望偏差可以写作 $h^{-1}$ 乘以 $\left|P(X_i\in [b_k,b_{k+1}))-h{f}_X(x)\right|$ ，其中 $P(X_i\in [b_k,b_{k+1}))$ 是样本点落在箱 $[b_k,b_{k+1})$ 内的概率。

4. 因为 $P(X_i\in [b_k,b_{k+1}))$ 等价于在箱 $[b_k,b_{k+1})$ 上 $f_X(y)$ 的积分，我们可以将期望偏差进一步转换为 $h^{-1}$ 乘以 $\left|{\int }_{b_k}^{b_{k+1}}{f}_X(y)dy-h{f}_X(x)\right|$ 。

5. 当应用利普希茨连续性的条件时，我们可以将 $f_X(y)$ 与 $f_X(x)$ 之间的差异 $|f_X(y)-f_X(x)|$ 限制在 $L|y-x|$ 以内。

6. 因此，整个积分的绝对值，也就是期望偏差，可以被限制在 $hL$ 以下。

这表明，如果真实密度函数 $f_X(x)$ 是利普希茨连续的，那么直方图估计器的偏差可以被控制，并且与箱宽 $h$ 成正比。换句话说，**箱宽越小，偏差可能越小，但这同时可能会增加方差。**这是统计学中所谓的“偏差-方差权衡”（bias-variance tradeoff）。

公式 $\left|E[{\hat{f}}_n(x)]-f_X(x)\right|=hL$ 的解释是关于直方图估计的偏差。这里， $E[{\hat{f}}_n(x)]$ 表示估计的概率密度函数在 $x$ 点的期望值， $f_X(x)$ 是真实的概率密度函数在 $x$ 点的值。我们希望这两个值尽可能接近，但由于估计是基于有限的样本数据，因此会存在一定的偏差。
在公式推导中， $h$ 是直方图中每个箱子的宽度， $L$ 是利普希茨常数，它限制了概率密度函数 $f_X(y)$ 的变化速度。假设 $f_X$ 在每个箱子的区间 $[b_k,b_{k+1})$ 内变化不是很剧烈，则该区间内的最大变化不会超过 $Lh$ （即利普希茨常数乘以箱宽）。

公式 $\left|E[{\hat{f}}_n(x)]-f_X(x)\right|=hL$ 的意义在于：

它提供了直方图估计误差的一个上界，即偏差不会超过 $hL$ 。

偏差 $hL$ 直接与箱宽 $h$ 相关：箱宽越小，每个箱子内的数据点越少，理论上偏差也越小。但箱宽过小可能导致样本中的随机波动增加，影响整体估计的稳定性。

这个性质在实践中非常有用，因为它意味着**我们可以通过减小箱宽 ( h ) 来减小估计的偏差，但是同时，较小的箱宽可能会增加随机波动（即方差）。**因此，选择箱宽需要在偏差和方差之间找到平衡点，这就是所谓的偏差-方差权衡。

直方图估计的方差（variance）

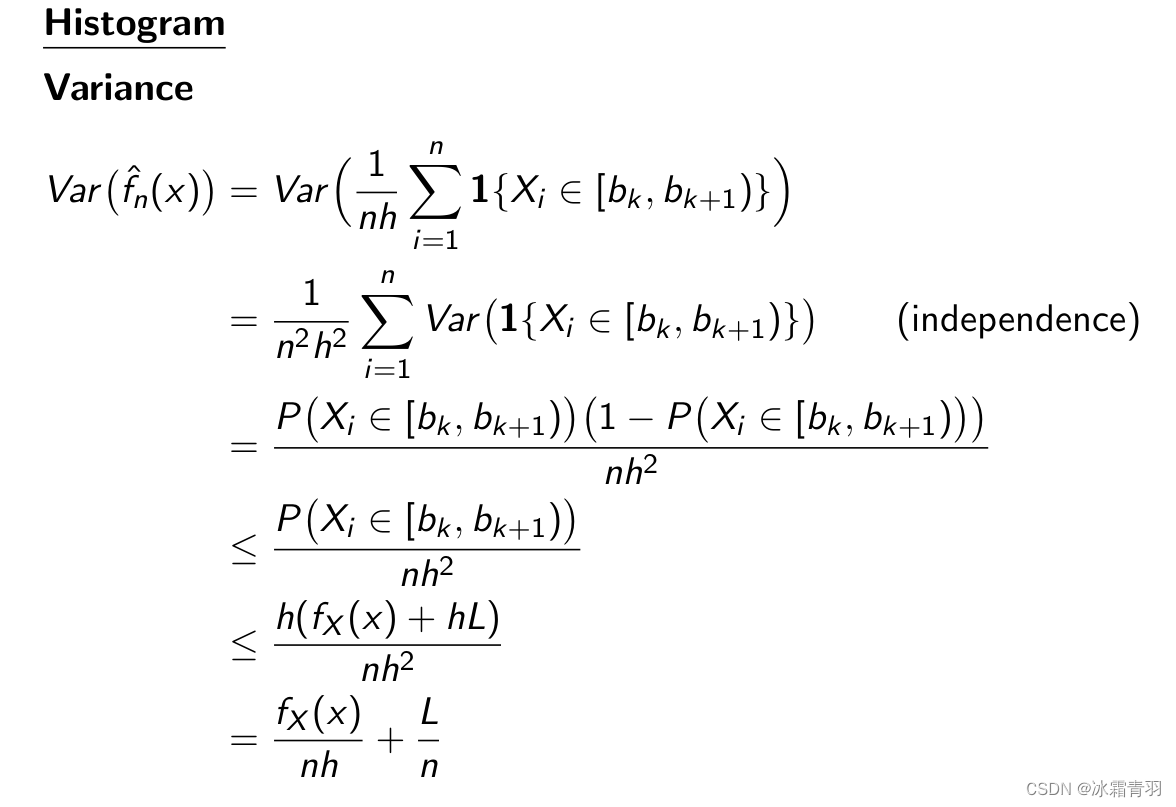
这张幻灯片讨论了直方图估计器的方差。方差是衡量估计器或随机变量波动程度的一个度量，可以被理解为估计值的稳定性。对于直方图来说，方差给出了在不同样本数据集上重复实验时，估计概率密度值的变化程度。

幻灯片上的公式是计算点 $x$ 在直方图估计器 ${\hat{f}}_n(x)$ 方差的推导。以下是推导的步骤：

1. 首先，方差的定义是 V a r ( f ^ n ( x ) ) = V a r ( 1 n h ∑ i = 1 n 1 { X i ∈ [ b k , b k + 1 ) } ) Var(\hat{f}_n(x))=Var(\frac{1}{nh}\sum_{i=1}^{n}1\{X_i\in[b_k,b_{k+1})\}) Var(f^​n​(x))=Var(nh1​∑i=1n​1{Xi​∈[bk​,bk+1​)}) ，这里 1 { X i ∈ [ b k , b k + 1 ) } 1\{X_i\in[b_k,b_{k+1})\} 1{Xi​∈[bk​,bk+1​)} 是一个指示函数，当 $X_i$ 落在箱子 $[b_k,b_{k+1})$ 里时取值为1，否则为0。

2. 因为样本是独立同分布的，可以将方差的和写为方差的总和乘以常数 $\frac{1}{n^2{h}^2}$ 。
   3. 每个指示函数的方差是 V a r ( 1 { X i ∈ [ b k , b k + 1 ) } ) = P ( X i ∈ [ b k , b k + 1 ) ) × ( 1 − P ( X i ∈ [ b k , b k + 1 ) ) ) Var(1\{X_i\in[b_k,b_{k+1})\})=P(X_i\in[b_k,b_{k+1}))\times(1-P(X_i\in[b_k,b_{k+1}))) Var(1{Xi​∈[bk​,bk+1​)})=P(Xi​∈[bk​,bk+1​))×(1−P(Xi​∈[bk​,bk+1​))) 。

3. 因为 $P(X_i\in [b_k,b_{k+1}))$ 可以被 $f_X(x)h$ 近似，我们得到 $Var({\hat{f}}_n(x))\le \frac{f_X(x)h+h^{2}L}{n{h}^2}$ 。

4. 最终，我们得到 $Var({\hat{f}}_n(x))=\frac{f_X(x)}{nh}+\frac{L}{n}$ ，这表明方差由两部分组成：一部分与 $\frac{1}{nh}$ 成正比，另一部分与 $\frac{1}{n}$ 成正比。
   方差的第一项 $\frac{f_X(x)}{nh}$ 反映了直方图在 $x$ 点的波动程度与样本数量 $n$ 和箱宽 $h$ 有关。随着样本数量的增加，或箱宽的减小，方差会减少。第二项 $\frac{L}{n}$ 与样本量 $n$ 有关，但与箱宽 $h$ 无关，表示即使箱宽不变，增加样本量也可以减小方差。

这个推导揭示了在选择直方图的箱宽时需要考虑的偏差-方差权衡。**箱宽 ( h ) 较小会导致偏差减小但方差增大，而箱宽较大则可能导致方差减小但偏差增大。**这是因为小箱宽虽然更能贴近数据的真实分布，**但同时每个箱子中的样本点会减少，导致估计的波动增大。**在实际应用中，选择一个恰当的箱宽既要考虑直方图的平滑度，也要尽量减少随机波动。

这张幻灯片汇总了我们之前讨论的关于直方图估计器的偏差和方差的内容，并提出了一个定理。定理表述了当我们有一个独立同分布（i.i.d.）样本，并且其概率密度函数 $f_X$ 在某个区间上满足利普希茨连续性条件时，直方图估计器 ${\hat{f}}_n$ 的偏差和方差的界限。

这个定理提供了两个不等式：
1. 偏差的绝对值的上限是 $hL$ ，这里 $h$ 是箱宽， $L$ 是利普希茨常数。
2. 方差的上限是 $\frac{f_X(x)}{nh}+\frac{L}{n}$ 。

幻灯片还说明了以下几点：

• ${\hat{f}}_n$ 是一个有偏估计器（biased estimator）。这意味着估计器的期望不一定等于真实的概率密度 $f_X(x)$ 。
• 要让估计器无偏，理论上箱宽 $h$ 必须为0，这在实践中是不可能的。
• 小的箱宽 $h$ 意味着小的偏差但大的方差。
• 大的箱宽 $h$ 意味着大的偏差但小的方差。
• 我们需要选择一个好的箱宽 $h$ ，这样既能保持偏差较低，又能控制方差，这就是所谓的偏差-方差权衡（bias-variance trade-off）。

最后一点提到，偏差-方差权衡在统计学中很常见，例如在岭回归（ridge regression）和最小绝对收缩选择算子（LASSO）等正则化技术中也会遇到。这些方法通过在损失函数中加入一个惩罚项来限制模型的复杂度，从而在偏差和方差之间找到一个平衡点。直方图在选择箱宽时面临类似的决策。