整式递推数列

详见钟子谦IOI2019国家集训队论文。
对于无限数列 { a i } \{a_i\} {ai​}和有限多项式数列 { P i } \{P_i\} {Pi​}满足$P_0$非$0$多项式。
若对任意 p > = ∣ { P } ∣ − 1 p>=|\{P\}|-1 p>=∣{P}∣−1有 ∑ i = 0 ∣ { P } ∣ − 1 a p − i P i ( p ) \sum_{i=0}^{|\{P\}|-1} a_{p-i}P_i(p) ∑i=0∣{P}∣−1​ap−i​Pi​(p)
则称$P$为$a$的整式递推式。
对于有限数列 { a i } \{a_i\} {ai​}也有此定义。
但是整式递推数列只指可以用$P$描述的无限数列 { a i } \{a_i\} {ai​}
举例：卡特兰数。
$C_n=\frac{4n-2}{n+1}{C}_{n-1}$
即
$C_n(n+1)-C_{n-1}(4n-2)=0$
所以$P_0(x)=x+1$，$P_1(x)=2-4x$的有限多项式数列 { P 0 , P 1 } \{P_0,P_1\} {P0​,P1​}即为卡特兰数的整式递推式。

整式递推式 { P i } \{ P_i \} {Pi​}的阶数为$|P|-1$，其次数为${\max }_{i=0}^{|P|-1}\mathrm{deg}{P}_i$。

微分有限：多项式$A(x)$为微分有限的当且仅当存在有限多项式数列 { Q } \{Q\} {Q}，
满足$Q_{|Q|-1}\ne 0$（注意我们的数列都是从$0$开始编号的，所以这句话的意思是最后一项非$0$），
且${\sum }_{i=0}^{|Q|-1}{Q}_i(x)A^{(i)}(x)=0$（其中$A^{(i)}(x)$为$A(x)$关于$x$的$i$次导数）。

代数形式幂级数：先通过那模糊的论文一句话描述猜测：
$A(x)$为代数形式幂级数的意思是$A(x)$是一个方程的根。
这个方程的解是多项式$A(x)$
也就是形如${\sum }_{i=0}{K}_i(x)f(x)=0$，其中$K_i(x)$是有理分式(多项式除多项式)。
最后解出来是$f(x)=A(x)$。
如果存在这样一个方程那么$A(x)$就是代数形式幂级数。
也就是$A(x)$在有理分式域上是代数的（但是并不代表$A(x)$是有理分式，但他也可以是）。

定理2.1：
无限数列 { a } \{a\} {a}的普通生成函数为$A(x)$，那么其为整式递推数列当且仅当$A(x)$为微分有限的。
证明：
1.充分性：
如果有${\sum }_{i=0}^m{Q}_i(x)A^{(i)}(x)=0$
发现$A^{(i)}(x)$其实和$A(x)x^{-i}$就是每一项上差一点系数。
推推式子就可以通过$Q_i(x)$推出其整式递推式。
2.必要性：
发现$A^{(i)}(x)$其实和$A(x)x^{-i}$就是每一项上差一点系数。
推推式子就可以通过$P_i(x)$推出使其满足微分有限的有限多项式序列$Q_i(x)$
（不是伪证吧。）

代数形式幂级数均为微分有限的。
（伪）证明：
引理：考虑多项式向量（更严谨的说法是：多项式构成了一个向量空间。）
那么$A(x)$的任意导数那么多个多项式，他们构成的向量空间维数有限，假设为$k$，那么对于$A(x),A^{\prime }(x),A^{\prime \prime }(x)...A^{(k)}(x)$他们这$k+1$个向量（多项式）就一定线性相关，可以给出一个他们的线性组合$Q_i(x)$使得${\sum }_{i=0}^k{Q}_i(x)A^{(i)}(x)=0$

首先对于简单的$f(x)=x$之类的我们可以 （由上一条引理）显然发现他们是微分有限的。

然后我们可以得到对于微分有限形式幂级数$u(x)$和代数形式幂级数$v(x)$，$u(v(x))$在其常数项收敛的意义下（形式幂级数复合常数项不收敛就构不成形式幂级数），也是微分有限的，然后就可以数归地证明所有形式幂级数均为微分有限的。

应用层面：
求出一个数列的整式递推式。

感觉，。；

例题：

首先我们可以得到一个$O(n^5)$左右的大力$DP$

然后打出表来之后我们可以。
去这里白嫖zzq的模板
然后求出$n<=1e6$的范围的答案。
。。。
参考代码：

#include<bits/stdc++.h>
#define mod 998244353
#define LL long long
#define rep(i,j,k) for(int i=(j),LIM=(k);i<=LIM;i++) 
using namespace std;

int Pow(int b,int k){ int r=1;for(;k;k>>=1,b=1ll*b*b%mod) if(k&1) r=1ll*r*b%mod; return r; }
vector<vector<int> > find_rel(
const vector<int>& ini,int deg)
{
	int n=ini.size(),B=(n+2)/(deg+2),C=B*(deg+1),R=n-(B-1);
	assert(B>=2&&R>=C-1);
	vector<vector<int> > mat(R,vector<int>(C));
	for(int i=0;i<R;++i)
		for(int j=0;j<B;++j)
			for(int k=0,x=ini[i+j]%mod;k<=deg;++k)
				mat[i][j*(deg+1)+k]=x,x=x*(LL)(i+j)%mod;
	int c=0;
	for(int i=0;i<C;++i)
	{
		int p=-1;
		for(int j=c;j<R;++j) if(mat[j][i]) {p=j; break;}
		if(p==-1) break;
		swap(mat[p],mat[c]);
		LL w=Pow(mat[c][c],mod-2);
		for(int j=i;j<C;++j) mat[c][j]=mat[c][j]*w%mod;
		for(int j=c+1;j<R;++j) if(mat[j][i]) //not fully eliminated
		{
			LL t=mat[j][i];
			for(int k=i;k<C;++k)
				mat[j][k]=(mat[j][k]-mat[i][k]*t)%mod;
		}
		++c;
	}
	assert(c!=C);
	for(int i=c-1;i>=0;--i) if(mat[i][c])
		for(int j=i-1;j>=0;--j)
			mat[j][c]=(mat[j][c]-mat[i][c]*(LL)mat[j][i])%mod;
	int od=c/(deg+1);
	vector<vector<int> > ret(od+1,vector<int>(deg+1));
	ret[0][c%(deg+1)]=1;
	for(int i=c-1;i>=0;--i)
		ret[od-i/(deg+1)][i%(deg+1)]=-mat[i][c];
	for(int i=0;i<=od;++i)
	{
		vector<int> tmp(deg+1);
		for(int k=0;k<=deg;++k)
		{
			LL S=1;
			for(int j=k;j<=deg;++j)
				tmp[k]=(tmp[k]+S*ret[i][j])%mod,
				S=S*(-i)%mod*(j+1)%mod*Pow(j+1-k,mod-2)%mod;
			tmp[k]=(tmp[k]%mod+mod)%mod;
		}
		ret[i]=tmp;
	}
	return ret;
}
int a[4][100005]={{0,0,1,9,55,290,1418,6629,30091,133806,586054,2537370,10886566,46369284,196323476,827082029,474985712,528106312,541758386,595828051,59377087,109000449,755534195,558578043,332657763,629563085,615306569,60402678,105929548,493601184,189333986,389953147,797915382,481229189,420292720,995685669,560845133,516975474,972593286,537377753,364690619,508809028,207371388,387442055,595552026,675655967,43409867,610503018,995841202,883699315,167313459}, {0,0,0,0,14,149,1054,6236,33398,167990,809664,3784560,17289420,77603161,343494418,-493097854,-468248033,104095918,157010208,-115880831,831488755,64373852,112711345,-491592039,-127489852,-177098602,-266045469,233150578,-12173954,294233090,-187126183,134746385,-321149993,-148345218,465153584,-44795846,-533979392,-305848929,-28957884,-253196987,539610500,-254944522,505585010,450780534,-246076482,-32472303,811346038,-265758912,-670036911,-362311751,634820484}, {0,0,0,0,3,98,1074,8245,52812,303340,1621010,8232983,40276667,191487706,-107998677,72391037,327327922,-507090862,-311407461,258624519,-561066175,365152019,-692593286,66360168,507909062,381762652,-248265301,351446733,647281286,-537110773,629992197,-93817477,-406946020,-79571376,-482899551,-44057130,820178765,637207205,-889827567,12730960,-400770744,-237003144,182901450,-795696960,321057984,-451718838,-436709246,353485690,563895810,126132164,-671112947}, {0,0,0,0,0,21,484,5430,44472,304997,1867456,10573956,56564788,289885815,438658583,946463028,822984448,341838670,633606596,893811591,27160201,979478338,875209020,580102669,528317334,663671805,285229136,454142107,887552094,642070688,437542901,898440781,100405302,511509010,392851051,161580714,175762226,863850977,529597727,669267529,559836197,946462699,428001404,55115645,513632905,181210615,146227845,802185240,453391893,421254118,891837190} };
vector<int>v[4]={vector<int>(a[0],a[0]+50),vector<int>(a[1],a[1]+50),vector<int>(a[2],a[2]+50),vector<int>(a[3],a[3]+50)};

int main(){
	int n,m;scanf("%d%d",&n,&m);
	vector<vector<int> >r=find_rel(v[m],7);
	printf("%d\n",r.size());
	rep(i,49,n){
		int s=0;
		rep(k,1,r.size()-1){
			vector<int>&u=r[k];
			int t=1;
			rep(j,0,u.size()-1){
				s=(s-1ll*t*a[m][i-k]%mod*u[j])%mod;
				t=1ll*t*i%mod;
			}
		}
		vector<int>&u=r[0];
		int t=1,sm=0;
		rep(j,0,u.size()-1){
			sm=(sm+1ll*t*u[j])%mod;
			t=1ll*t*i%mod;	
		}
		a[m][i]=Pow(sm,mod-2)*1ll*s%mod;
	}
	printf("%d\n",(a[m][n]+mod)%mod);
}

留tag：这个模板我想把它压到20行以内，
但是我不懂它在写些什么。。。

所以，今天开始啃Enumerative Combinatorics Volume 2:第6章。

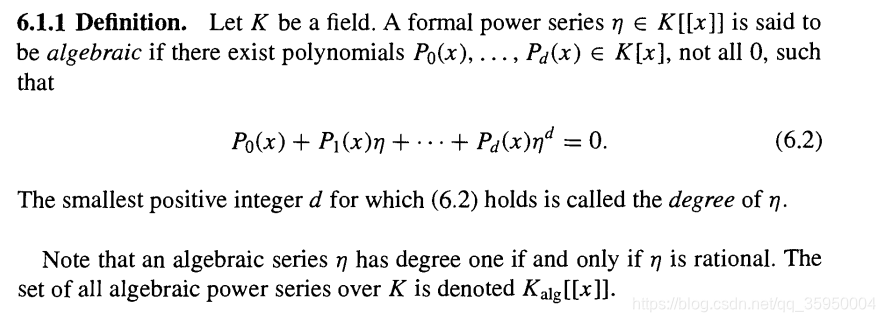
这是有理分式的定义，指一个形式幂级数可以被表示为一个一次幂级数方程的根。

所以有理分式域就是拓展拉格朗日反演证明里那个奇怪的域？

来啦来啦代数形式幂级数、

开始了，$D-finite$微分有限$P-recursive$多项式递归函数大赏。

但是$u_1,u_2,u_4$不是$D-finite$的。。。

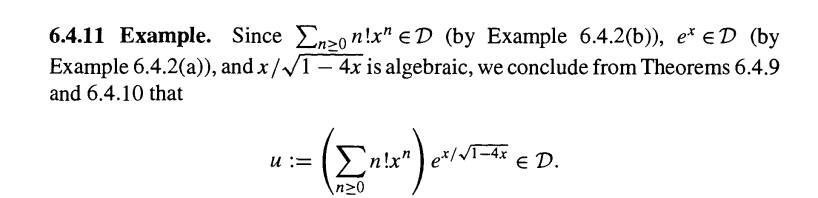
复合法则。

撒花！
终于压进20行了。
顺便说下$zzq$那不觉明历的写法是什么意思。
首先我们需要把待定的整式递推式倒过来写（论文应该是打错了字），建立每个$a_i$和之后若干 （$B-1$）个的整式方程，于是形如${\sum }_{i=0}^{B-1}{a}_{k+i}{Q}_{B-1-i}=0$，这是因为我们不知道求出的最短整式递推式长度是多少，换成从前到后的形式可以保证不管求出的整式递推式长度为多少，对于前面几项它都应该是满足的，如果从后往前那么就有不满足前面几项的可能。
然后就直接高斯消元？
但是你要发现，我们这些方程的右边都是$0$。
稍微学学线性代数的入门课程即可发现，我们需要的是一个非平凡解（就是非全$0$解），而在这种方程组中非平凡解存在就必须要有自由元，其构成的矩阵不满秩。
那么我们按翻转后的$Q$数组从前往后高斯消元，那么得到一个自由元时，前面的子矩阵就是最小的不满秩前缀矩阵（语无伦次）。
那么我们把这个最小的不满秩前缀矩阵，令其中唯一的自由元为1。
注意这个自由元对应在${\sum }_{i=0}^{B-1}{a}_{k+i}{Q}_{B-1-i}=0$中应该是$Q_0$中的一个$x^k$前的系数。
这时把前面的元都解出来可以得到$Q$，再二项式定理得到$P$即可。
注意这时求出的很有可能是该次数下最小阶的（最短的）。
可能求出多个阶数不同的整式递推式，但是阶数变短是需要次数提升作为代价的。
另外模板里确定$B$的那个奇怪的式子是$\mathrm{M}\mathrm{i}{\mathrm{n}}_{25}$提出来的。（我也不太懂日语）

20行模板：

#include<bits/stdc++.h>
#define mod 998244353
#define LL long long
#define rep(i,j,k) for(int i=(j),LIM=(k);i<=LIM;i++) 
#define per(i,j,k) for(int i=(j),LIM=(k);i>=LIM;i--)
#define vc vector
#define vi vc<int>
#define Ct const
using namespace std;

int Pow(int b,int k){ int r=1;for(;k;k>>=1,b=1ll*b*b%mod) if(k&1) r=1ll*r*b%mod; return r; }
vc<vi>PR(Ct vi &a,int D){ // P-recursive , a[0~a.size()-1] is usd
	int N=a.size(),B=(N+2)/(D+2),C=B*(D+1),R=N-(B-1),c;
	vc<vi>b(R,vi(C));
	rep(i,0,R-1) rep(j,0,B-1) for(int k=0,pw=a[i+j];k<=D;k++,pw=(LL)pw*i%mod) b[i][j*(D+1)+k]=pw;
	rep(i,0,C-1){
		int p=-1;rep(j,i,R-1) if(b[j][i]) {p=j;break;}
		if(p==-1){ c=i;break;}swap(b[i],b[p]);
		p=Pow(b[i][i],mod-2);rep(j,i,C-1) b[i][j]=(LL)b[i][j]*p%mod;
		rep(j,i+1,R-1) if(p=b[j][i]) rep(k,i,C-1) b[j][k]=(b[j][k]-(LL)b[i][k]*p)%mod; 
	}assert(c^C);
	int M=c/(D+1)+1;
	per(i,c-1,0) if(b[i][c]) rep(j,0,i-1) b[j][c]=(b[j][c]-(LL)b[j][i]*b[i][c])%mod;
	vc<vi>r(M,vi(D+1));vi t(D+1);
	rep(i,(r[0][c%(D+1)]=1,0),c-1) r[M-i/(D+1)-1][i%(D+1)]=-b[i][c];
	for(int i=0,S;i<M;r[i]=t,t=vi(D+1),i++)
		rep(j,0,D) rep(k,(S=1,j),D){
				t[j]=(t[j]+(LL)S*r[i][k])%mod;
				S=(LL)S*(-M+1)%mod*(k+1)%mod*Pow(k-j+1,mod-2)%mod;
			}
	return r;
}

快速求整式递推数列的第$n$项：
看洛谷的【模板】整式递推