机器学习进阶（Foundation of Machine Learning）-1

前言

最近刚刚上研究生方向是NLP，但看了很多机器学习方面的书比如西瓜书等等，总觉得不是很基础和系统，最后选择了这本教材（Foundation of Machine Learning）来啃。因为是第一次想要系统性地写一些博客，所以打算把学习笔记写在博客上。这本书才看到前三章，但是整体感觉很基础，很多推导，有些要理解起来也会比较困难，所以写成博客也方便讨论。这个系列也算是记录我自己对于这本书的思考和理解吧，后续这个系列应该会加入一些其他的关于机器学习的拓展知识。

Introduction

机器学习可以被定义为一种利用经验来进行准确预测的计算方法，因此机器学习的算法一方面需要考虑效率，一方面则需要考虑精度。对于效率的考虑除了空间时间复杂度以外，必须考虑的是样本空间的复杂性。事实上，算法效率的边界受到假设集与数据空间的影响。此处一些假设集等符号定义以及在线学习、强化学习等问题定义不提。

PAC学习框架

PAC学习框架是通过实现近似解所需的样本点个数、样本复杂性、学习算法的时间空间复杂度来定义概念集是否可学习的。即明确什么问题是可以高效学习的，什么问题难以学习、达到一定的精度需要多少样本等问题。
因此一个问题是否PAC可学习的有如下定义：
其中$R(h_S)$代表在观察到采样出的大小为$m$的样本集$S$后，算法给出的映射函数$h$的错误次数，可以看到这个式子综合了精度与样本空间大小，假设映射函数空间以及映射函数的计算复杂度的大小。而映射函数$h$的错误次数可以利用该函数在样本空间$S$上的经验误差来估计。这里对于样本分布$D$有样本独立性假设。

例如证明一个矩阵空间拟合问题是PAC可学习的：
即假设集是平面矩阵的集合，在二元问题上可以认为映射函数就是矩阵内的点label为1，其余为0. 如下图，若目标函数为$R$,则$R^{\prime }$的误差包括除它们交集之外的$R$内的点以及$R^{\prime }$内的点：

为了证明这个问题是PAC可学习的，那么就需要找到一个算法满足上述定义。设计一个算法：对于每次采样的$S$,返回包含所有正例点的矩形：

假设空间中的点落在$R$中的概率大于$ϵ$,即$P(R)>ϵ$。基于R的四条边向内扩展，能够分出四块区域，对这四块区域限制大小（即点落入的概率）小于$ϵ/4$,即：

由于$R^{\prime }$是包含在$R$内的，它的出错情况只可能出现在点落在$R$内但是在$R^{\prime }$外的时候，同时又由于$R^{\prime }$是一个矩形，因此如果$R^{\prime }$的出错概率大于$ϵ$，$R^{\prime }$至少和上述四个区域中的一个没有交集。因为如果都有交集，$R$内$R^{\prime }$不覆盖的区域，即出错情况的概率，必然是小于$4\ast ϵ/4$的。因此：

其中最后一个不等式转化使用到了$1-x<=e^{-x}$不等式。因此令$m>=\frac{4}{ϵ}\log \frac{4}{\delta }$,有$P_{S\sim D^m}[R(R_s)>ϵ]<=\delta$，m是多项式的，因此得证。

有限假设集一致情况下的样本复杂度边界

一致情况是指算法给出的映射函数能够保证在样本集上没有错误，就像矩形例子中算法给出的是包含所有正例的矩形一样。这种情况下有定理：

这里的证明采用的思路是证明在误差大于$ϵ$的假设函数集合中存在一个对所有大小为$m$的$S$满足经验误差为0的假设函数概率有上界。可以看到越多的样本对于算法的估计准确率是越有的。

有限假设集不一致情况下的样本复杂度边界

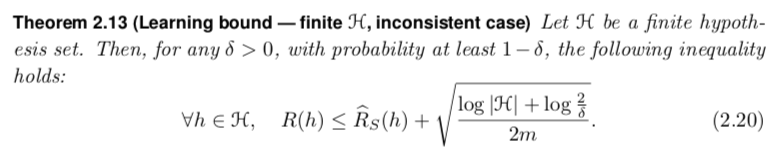
这里的证明用到了两个推论，第二个推论比较重要：

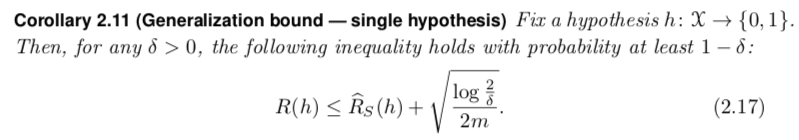
上界的证明直接用第1个推论能证到。这个上界其实是在假设集大小和样本大小之间的均衡，假设集大有助于减小经验误差，但是会对第二项有惩罚。

拓展

Agnostic PAC-learning

上述情况的映射是每个点只有一个预测值，现实生活中可能并不是这样。因此PAC学习拓展为Agnostic PAC-learning：

贝叶斯误差和噪声