2.4 泛化性
2.4.1 确定性与随机性情境
对于监督学习,分布D定义在X×Y\mathcal{X}\times\mathcal{Y}X×Y上,并且训练样本是根据D采样得到的i.i.d.的样本:
S={(x1,y1),⋯ ,(xm,ym)}S=\{(x_1,y_1),\cdots,(x_m,y_m)\}S={(x1,y1),⋯,(xm,ym)}学习的目的就是找到一个假设h∈Hh\in Hh∈H,使得泛化误差较小:
R(h)=Pr(x,y)∼D[h(x)≠y]=E(x,y)∼D[1(h(x)≠y)]R(h)=\mathop{Pr}\limits_{(x,y)\sim D}[h(x)\ne y]=\mathop{E}\limits_{(x,y)\sim D}[1(h(x)\ne y)]R(h)=(x,y)∼DPr[h(x)=y]=(x,y)∼DE[1(h(x)=y)]更一般的情境是随机性情境,学习算法输出的标签是输入的概率函数,输入对应的标签不是唯一的。
举个例子,比如对于人的特征长头发,男人占比10%,女人占比90%,那么在对这个特征预测性别时,学到的是一个概率的分布。
此时对于PAC学习就有了一个很自然的扩展——不可知PAC学习
令H为一个假设集。A是一个不可知PAC学习算法的条件是:存在一个多项式函数poly(⋅,⋅,⋅,⋅)poly(\cdot,\cdot,\cdot,\cdot)poly(⋅,⋅,⋅,⋅)使得对于任意 以及
以及 ,对于所有在
,对于所有在X×Y\mathcal{X}\times\mathcal{Y}X×Y上的分布D,对于满足m≥poly(1/ϵ,1/δ,n,size(c))m\ge poly(1/\epsilon,1/\delta,n,size(c))m≥poly(1/ϵ,1/δ,n,size(c))的任意样本规模有下面的不等式成立:
PrS∼Dm[R(hs)−minh∈HR(h)≤ϵ]≥1−δ\mathop{Pr}\limits_{S\sim D^m}[R(h_s)-\mathop{min}_{h\in H}R(h)\le \epsilon]\ge 1-\deltaS∼DmPr[R(hs)−minh∈HR(h)≤ϵ]≥1−δ进一步地,如果算法A\mathcal{A}A可在poly(1/ϵ,1/δ,n,size(c))poly(1/\epsilon,1/\delta,n,size(c))poly(1/ϵ,1/δ,n,size(c))内执行,则其可被称为一个高效的不可知PAC学习算法。
当一个样本的标签可以由某个唯一的可测函数f:X→Yf:\mathcal{X}\rightarrow\mathcal{Y}f:X→Y(以概率1成立)确定时,这种情境被称为确定性情境。
2.4.2 贝叶斯误差与噪声
首先明确一件事:对于确定性情境,存在一个没有泛化误差的目标函数f\mathcal{f}f使得R(h)=0R(h)=0R(h)=0,对于随机性情境,对于任意假设,存在一个最小的非0误差。
贝叶斯误差:给定一个在X×Y\mathcal{X}\times\mathcal{Y}X×Y上分布D,相应的贝叶斯误差R∗R^{ * }R∗定义为由可测函数类h:X→Yh:\mathcal{X}\rightarrow\mathcal{Y}h:X→Y产生的误差下界:
R∗=infh measurableR(h) R^{ * }=\mathop{inf}\limits_{h\;measurable}R(h) R∗=hmeasurableinfR(h)一个满足R(h)=R∗R(h)=R^{*}R(h)=R∗的假设h\mathcal{h}h被称为贝叶斯假设或贝叶斯分类器。
根据定义,对于确定性的情境,我们有R∗=0R^{ * }=0R∗=0,但是对于随机性情境,R∗≠0R^{ * }≠0R∗=0。进一步地,贝叶斯分类器hbayesh_{bayes}hbayes可以用条件概率进行定义:
∀x∈X,hBayes(x)=argmaxy∈[0,1]Pr[y∣x]\forall x\in X,h_{Bayes}(x)=\mathop{argmax}\limits_{y\in[0,1]}Pr[y|x]∀x∈X,hBayes(x)=y∈[0,1]argmaxPr[y∣x]这里举一个上一个例子帮助理解,当我们此时有一个长头发的人时,我们有10%的概率预测其为男性,90%的概率预测其为女性,那么根据贝叶斯最优分类器的定义,我们会认为其为女性,但是这样的判断也仅仅是根据概率分布来的,但是会存在误差,这个误差无法避免,这就是贝叶斯误差。
hbayesh_{bayes}hbayes在x∈Xx\in \mathcal{X}x∈X的平均误差为min{Pr[0∣x],Pr[1∣x]}min\{Pr[0|x],Pr[1|x]\}min{Pr[0∣x],Pr[1∣x]},这是最小的,可能误差。
噪声:给定一个在X×Y\mathcal{X}\times\mathcal{Y}X×Y上的分布D,在样本点x∈Xx\in \mathcal{X}x∈X上的噪声定义为:
noise(x)=min{Pr[1∣x],Pr[0∣x]}noise(x)=min\{Pr[1|x],Pr[0|x]\}noise(x)=min{Pr[1∣x],Pr[0∣x]}则平均噪声或称关于分布D的噪声为E[noise(x)]E[noise(x)]E[noise(x)]。
平均噪声严格的等于贝叶斯误差:noise=E[noise]=R∗noise=E[noise]=R^{*}noise=E[noise]=R∗。可以将噪声看作对学习任务难易程度的刻画。对于一个样本点x∈Xx\in \mathcal{X}x∈X,若noise(x)noise(x)noise(x)接近1/2,则往往被称为噪点,对这种点的精确预测也是极具挑战性的。
2.4.3 估计误差与近似误差
对于一个假设h∈Hh\in Hh∈H的误差和贝叶斯误差,按如下分解二者之差:
R(h)−R∗=R(h)−R(h∗∗)⏟估计误差+R(h∗)−R∗∗⏟近似误差R(h)-R^{ * }=\underbrace{R(h)-R(h^{ **})}_{估计误差}+\underbrace{R(h^{ * })-R^{ **}}_{近似误差}R(h)−R∗=估计误差
R(h)−R(h∗∗)+近似误差
R(h∗)−R∗∗其中,h∗h^ *h∗表示H中误差最小的假设,或者称为类中最优假设(best-in-class hypothesis)
第一项指的是估计误差,该误差依赖于所选定的假设hhh,衡量的是选定的假设与类中最优假设的相近程度,不可知PAC学习的定义便是基于此。
对于算法A\mathcal{A}A,其估计误差是指其根据训练样本集SSS产生的假设hsh_shs的估计误差,这种误差有时可以由泛化误差界定。
例如,令hsERMh_s^{ERM}hsERM表示具有最小经验误差的假设,其估计误差推理如下:

第二项指的是近似误差,衡量的是用H对贝叶斯误差的近似程度,可以看作是假设集H的一个性质,衡量假设集H的丰富程度。并且近似误差在实际中无法求出,因为潜在分布是未知的。
2.4.4 模型选择
我们有了问题的设定,有了训练集的加持,也有了对于最终误差的一个大致估计,选择算法模型的时候,什么样的模型才是一个合理的,在保证精度的同时还能降低复杂度,下面就是模型选择的理论基础。
选择算法模型时应该考虑算法的两个属性:经验误差以及复杂度项。
对于ERM算法,即经验风险最小化算法,其考虑的是找到一个在训练集上误差最小的假设:
hsERM=argminh∈HR^s(h)h_s^{ERM}=\mathop{argmin}\limits_{h\in H}\hat{R}_s(h)hsERM=h∈HargminR^s(h)但是却忽视了复杂度项,往往表现的一般。另一种策略是SRM算法,即结构风险最小化,考虑的是一个势不断增长的无线假设集序列:
H0⊂H1⊂⋯Hn⋯H_0\subset H_1\subset\cdots H_n\cdotsH0⊂H1⊂⋯Hn⋯并对每个HnH_nHn对应的ERM解hnERMh^{ERM}_nhnERM,最终从这些解hnERMh^{ERM}_nhnERM中选择一个假设,使得经验误差和复杂度项complexity(Hn,m)complexity(H_n,m)complexity(Hn,m)(依赖样本规模m和假设集HnH_nHn的大小)或者说是假设集HnH_nHn的容纳性(capacity,丰富程度的另一种度量)的和最小:
hsSRM=argminh∈H,n∈NR^s(h)+complexity(Hn,m)h_s^{SRM}=\mathop{argmin}\limits_{h\in H,n\in N}\hat{R}_s(h)+complexity(H_n,m)hsSRM=h∈H,n∈NargminR^s(h)+complexity(Hn,m)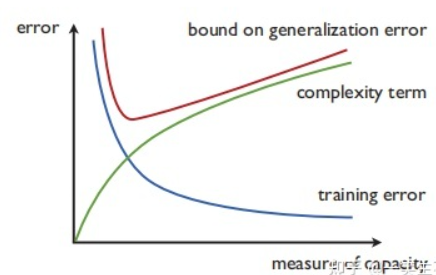
SRM有很强的理论保证,但是往往计算开销很大,因为要计算多个ERM问题,找到最小的那个。但是当误差为0时,不易计算无限多个,因为假设集的复杂度随n在递增,所以找到误差为0时可以停止。
当然存在一种替代的直接的优化,即最小化经验误差和正则项(regularization term,用于对更复杂的假设给予惩罚)之和。这里当H为向量空间时,正则项通常定义为∣∣h∣∣2||h||^2∣∣h∣∣2,即二范数:
hsERM=argminh∈HR^s(h)+λ∣∣h∣∣2h_s^{ERM}=\mathop{argmin}\limits_{h\in H}\hat{R}_s(h)+\lambda||h||^2hsERM=h∈HargminR^s(h)+λ∣∣h∣∣2其中λ\lambdaλ为正则因子,用于权衡经验误差和模型复杂度,很多算法的设计都是基于此。























 976
976

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








