深度学习--前馈神经网络

初入深度学习，有错的地方还请指正。
参考视频: 李宏毅深度学习， BP神经网络公式推导完整版
参考书籍：西瓜书，花书

前"馈神经网络"也叫"多层感知机"也叫"深度前馈网络"，是一种典型的深度学习模型。它的目的是近似某个函数。

感知机

感知机由两层神经元组成，一个是输入层，一个是输出层，如下图，左边的是输入层，右边的是输出层。
输出层是一个MP神经元，MP神经元会把输入的数据结合上他的权值，然后通过激活函数最后输出。
$x_1,x_2..x_n$就可以看成是特征。

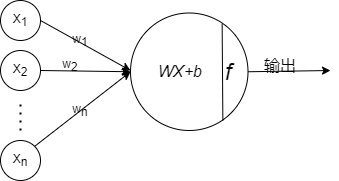
其中$WX+b$就是可以看做是一个一般超平面方程$WX+b=0$的左边，而激活函数呢，最经典的就是sigmoid函数他长这样

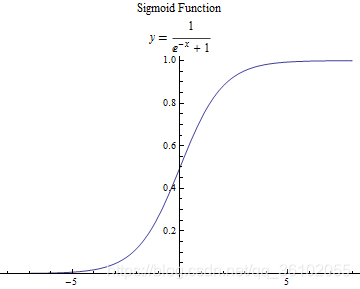
经过了它之后，输出的值就是$Sigmoid(WX+b)$，类似于逻辑回归他就可以做一些二分类问题。

但我们知道这样的模型解决问题能力很差，因为他只能解决线性可分问题，在传统机器学习中我们的解决方法有两种，一种是对输入的特征进行组合等改造，然后再扔给算法。另一种是直接在算法上做手脚，引入了核函数。通过这两种手段都可以使最终得到的模型是非线性的。

以上两种方法都是学习了一种映射$\varphi$，使用这种映射把原本的样本映射到一个新的样本空间去。
但是这样做有一定的局限性，那就是这种映射在不同的领域可能不一样，如何选择可能要靠经验。

而深度学习策略就是去学习这种映射，他从一个更加广泛地函数族中去进行寻找求解适合当前训练数据的映射。

回到上面可以看出，整个最核心进行工作的部分就是MP神经元，如果我们把神经元进行扩展，使它们相互之间进行链接，就得到了深度神经网络。

如果每个神经元只与前一层的神经元相连。接收前一层的输出，并输出给下一层．各层间没有反馈，那么这个网络就被称为前馈神经网络。

反向传播算法(Backpropagation)

给出一个神经网络，如何对其进行训练就是首先的问题，深度学习和传统机器学习一样，使用的也是梯度下降法。

前向传播

首先需要规定一些符号的表示：

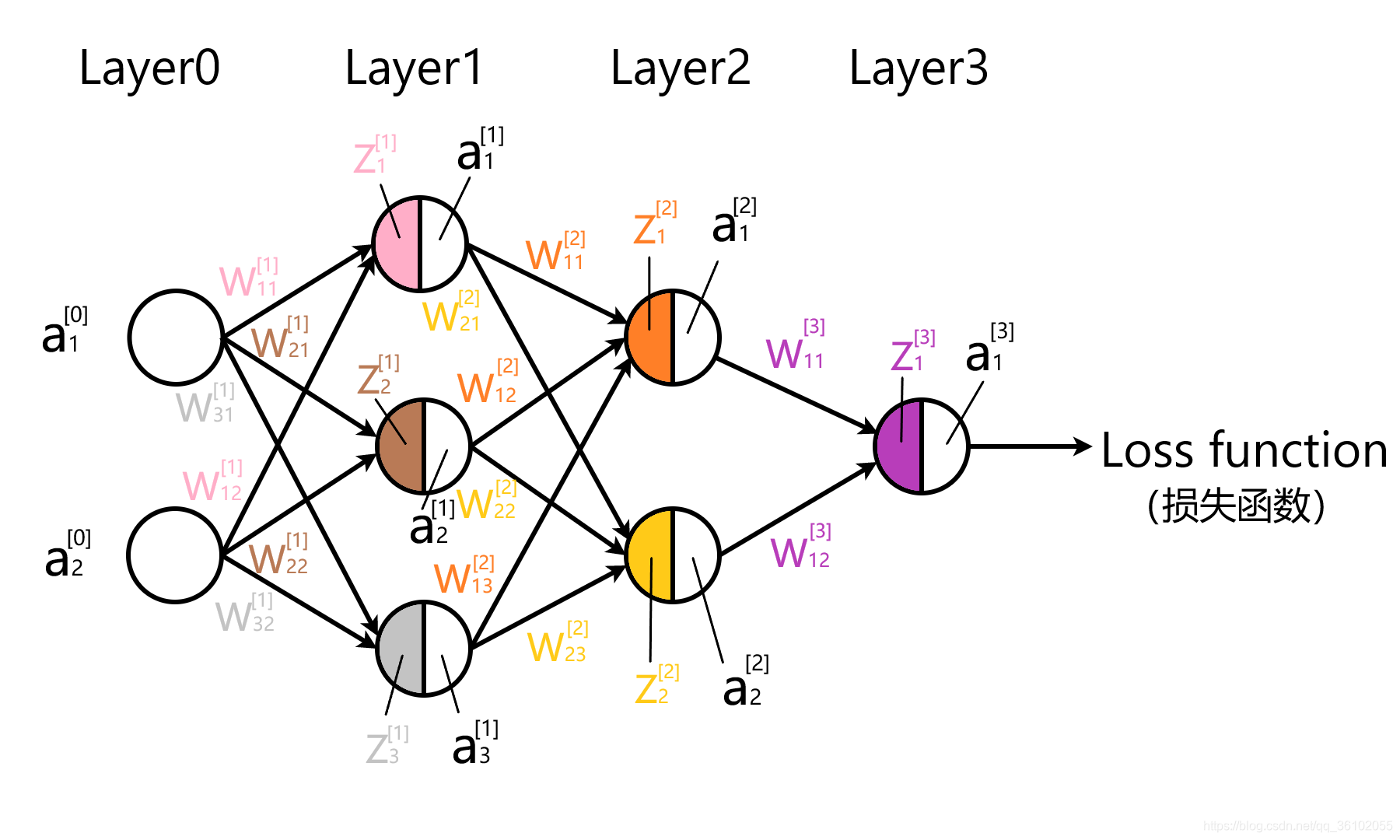
我们规定以下符号：

1. $w_{jk}^{[l]}$表示第l层中的第j个神经元与第$l-1$层中第k个神经元的连线，也就是权重。
2. $b_j^{[l]}$表示第$l$层中第j个神经元的截距。
3. $z_j^{[l]}$表示第$l$层第j个神经元乘以权重求和后的结果
4. $a_j^{[l]}$表示第$l$层第j个神经元的$z$经过激活函数后的结果。
5. $\sigma (x)$表示激活函数
   简单来说，有
   $$a_j^{[l]}=\sigma (z_j^{[l]})=\sigma (\sum _k{w}_{jk}^{[l]}{a}_k^{[l-1]}+b_j^{[l]})$$
   为了方便向量运算，所以我们用矩阵来表示权重，比如第1层的所有神经元的权重，我们把每个神经元的权重变成行向量，然后竖着排放它们。

$$w^{[1]}=\left[\begin{array}{l}{w}_1^{[1]}\\ w_2^{[1]}\\ w_3^{[1]}\end{array}\right]=\left[\begin{array}{lll}{w}_{11}^{[1]}& w_{12}^{[1]}& \\ w_{21}^{[1]}& w_{22}^{[1]}& \\ w_{31}^{[1]}& w_{32}^{[1]}& \end{array}\right]$$
同理我们也这样摆放b
$$b^{[1]}=\left[\begin{array}{l}{b}_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\end{array}\right]$$
于是就得到第1层的$z$
$$z^{[1]}=\left[\begin{array}{lll}{w}_{11}^{[1]}& w_{12}^{[1]}& \\ w_{21}^{[1]}& w_{22}^{[1]}& \\ w_{31}^{[1]}& w_{32}^{[1]}& \end{array}\right]\cdot \left[\begin{array}{c}{a}_1^{[0]}\\ a_2^{[0]}\end{array}\right]+\left[\begin{array}{l}{b}_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\end{array}\right]$$
即
$$z^{[1]}=w^{[1]}\cdot a^{[0]}+b^{[1]}$$
然后就可以得到
$$a^{[1]}=\sigma (z^{[1]})$$
整个前向传播核心就这两个式子，这样一层一层的推进，直到最后一层得到最终的输出，就完成了一次前向传播：
$$\begin{gathered} z^{[l]}=w^{[l]}\cdot a^{[l-1]}+b^{[l]} \\ {a}^{[l]}=\sigma (z^{[l]}) \end{gathered}$$

反向传播

反向传播比较复杂，首相需要明确目标，对于我们的代价函数L，我们想要求的是梯度，也就是偏导数：$\frac{\partial L}{\partial w_{jk}^{[l]}}$与$\frac{\partial L}{\partial b_j^{[l]}}$，在此之前我们需要求出一个中间的值，我们把其称作为$\delta$
我们定义：${\delta }_j^{[l]}=\frac{\partial L}{\partial z_j^{[l]}}$
然后我们看如何求出每一层的$\delta$

1. 对于输出层
   设输出层为第L层
   那么就有${\delta }_j^{[L]}=\frac{\partial L}{z_j^{[L]}}=\frac{\partial L}{\partial a_j^{[L]}}\frac{\partial a_j^{[L]}}{\partial z_j^{[L]}}=\frac{\partial L}{\partial a_j^{[L]}}{\sigma }^{\prime }(z_j^{[L]})$
   在实际训练时，输入的可能是多个数据，所以要用矩阵的来表示。
   在此处应该是$${\delta }^{[L]}=\frac{\partial L}{\partial a^{[L]}}\odot {\sigma }^{\prime }(z^{[L]})$$
   $\odot$表示矩阵中每个对应位置的元素相乘此时得到的矩阵${\delta }_j^{[L]}$形状为(len(L) x n)
   其中$len(L)$为第L层的神经元个数，n为一次训练输入的样本个数

2. 对于隐藏层
   $z_j^{[l+1]}=\sum _k{w}_{jk}^{[l+1]}\sigma (z_k^{[l]})+b_k^{[l+1]}$
   那么$\frac{\partial z_j^{[l+1]}}{\partial z_m^{[l]}}=w_{jm}^{[l+1]}\sigma (z_m^{[l]})$
   那么就有:
   ${\delta }_j^{[l]}=\frac{\partial L}{\partial z_j^{[l]}}=\frac{\partial L}{\partial z_k^{[l+1]}}\frac{\partial z_k^{[l+1]}}{\partial z_j^{[l]}}={\delta }_k^{[l+1]}{w}_{kj}^{[l+1]}{\sigma }^{\prime }(z_j^{[l]})$
   如果第l层的第j个节点传给了后面的多个节点那么此处的$\delta$为：
   ${\delta }_j^{[l]}=\sum _k{\delta }_k^{[l+1]}{w}_{kj}^{[l+1]}{\sigma }^{\prime }(z_j^{[l]})$
   写成矩阵的话就是
   $$\left[\begin{array}{lll}{w}_{11}^{[l+1]}& w_{21}^{[l+1]}...& w_{len(l+1)1}^{[l+1]}\\ w_{12}^{[l+1]}& w_{22}^{[l+1]}...& w_{len(l+1)2}^{[l+1]}\\ .& & \\ .& & \\ w_{1len(l)}^{[l+1]}& w_{2len(l)}^{[l+1]}...& w_{len(l)len(l+1)}^{[l+1]}\end{array}\right]\cdot \left[\begin{array}{lll}{\delta }_1^{[l+1](1)}& {\delta }_1^{[l+1](2)}...& {\delta }_1^{[l+1](n)}\\ {\delta }_2^{[l+1](1)}& {\delta }_2^{[l+1](2)}...& {\delta }_2^{[l+1](n)}\\ .& & \\ .& & \\ {\delta }_{len(l+1)}^{[l+1](1)}& {\delta }_{len(l+1)}^{[l+1](2)}...& {\delta }_{len(l+1)}^{[l+1](n)}\end{array}\right]\odot \left[\begin{array}{c}{\sigma }^{\prime }\left(z_1^{[l]}\right)\\ {\sigma }^{\prime }\left(z_2^{[l]}\right)\\ ⋮\\ {\sigma }^{\prime }\left(z_j^{[l]}\right)\end{array}\right]$$
   也就是${\delta }^{[l]}=W^{[l+1{]}^T}\cdot {\delta }^{[l+1]}\odot {\sigma }^{\prime }(z^{[l]})$
   其中
   $W^{[}l+1{]}^T$的shape为(len(l) X len(l + 1))
   ${\delta }^{[l+1]}$的shape为(len(l + 1) X n)
   ${\sigma }^{\prime }(z^{[l]})$的shape为(len(l) X n)
   最终输出shape为(len(l) X n)

3. 计算各个参数的偏导
   $z_j^{[l]}={\sum }_k{w}_{jk}^{[l]}{a}_k^{[l-1]}+b_k^{[l]}$
   $\frac{\partial L}{\partial b_j^{[l]}}=\frac{\partial L}{\partial z_j^{[l]}}\frac{\partial z_j^{[l]}}{\partial b_j^{[l]}}={\delta }_j^{[l]}$
   $\frac{\partial L}{\partial w_{jk}^{[l]}}=\frac{\partial L}{\partial z_j^{[l]}}\frac{\partial z_j^{[l]}}{\partial w_{jk}^{[l]}}=a_k^{l-1}{\delta }_j^{[l]}$
   把它们写成矩阵的形式就是这样的
   $\nabla \frac{\partial L}{\partial b^{[l]}}={\delta }^{[l]}$
   $\nabla \frac{\partial L}{\partial w^{[l]}}={\delta }^{[l]}\cdot a^{l-1^T}$

numpy简单实现一个全连接网络

首先，我要实现的网络结构如下

数据准备

首先，我们使用sklearn的鸢尾花数据集，如果不想用sklearn的可以自己造一个。
我们要做的是一个二分类问题，所以要对原本的数据进行改造。

from sklearn import datasets

iris = datasets.load_iris()
data = iris['data'][:, [1, 3]].T # 取出其中两个维度，并且转置
target = iris['target']
target[target == 2] = 1 # 把lable的种类变成2个

初始化参数

首先定义出一个常量区，这里用于规定每一层的神经元个数方便下面来初始化参数。
初始化参数通常把每个参数都初始化成一个很小的值，不能全部都初始化为0，这里使用正态分布来随机初始化。

# constants
n_input = 2
hid_layer_1 = 3
hid_layer_2 = 2
n_output = 1
# init parameters
np.random.seed(666)
weights = {
    'W1': np.random.normal(size=(hid_layer_1, n_input)),
    'W2': np.random.normal(size=(hid_layer_2, hid_layer_1)),
    'output': np.random.normal(size=(n_output, hid_layer_2))
}
biases = {
    'B1': np.random.normal(size=(hid_layer_1, 1)),
    'B2': np.random.normal(size=(hid_layer_2, 1)),
    'output': np.random.normal(size=(n_output, 1))
}

激活函数&成本函数

激活函数我们使用sigmoid函数，而成本函数我们使用MSE
我们最后的输出是$(0,1)$之间的值，而lable也是0或者1，所以可以用MSE来评估损失
$MSE=\frac{1}{2n}\sum _{i=1}^n(y^{(i)}-a^{[L](i)}{)}^2$
于是我们写出sigmoid函数的导数和函数

# activation function
def sigmoid(X):
    return 1 / (np.exp(-X) + 1)

def d_sigmoid(X):
    tmp = sigmoid(X)
    return tmp * (1 - tmp)

前向传播

根据前向传播公式，我们可以轻松地就算各个值
$$\begin{gathered} z^{[l]}=w^{[l]}\cdot a^{[l-1]}+b^{[l]} \\ {a}^{[l]}=\sigma (z^{[l]}) \end{gathered}$$

# forward propagation
def forward(X):
    h1 = sigmoid(np.dot(weights['W1'], X) + biases['B1'])
    h2 = sigmoid(np.dot(weights['W2'], h1) + biases['B2'])
    output = sigmoid(np.dot(weights['output'], h2) + biases['output'])
    return output
    
def forward_1(input_0): # 第一层的输出
    z = np.dot(weights['W1'], input_0) + biases['B1']
    a = sigmoid(z)
    return z, a

def forward_2(input_1): # 第二层
    z = np.dot(weights['W2'], input_1) + biases['B2']
    a = sigmoid(z)
    return z, a

def forward_3(input_2): # 输出层
    z = np.dot(weights['output'], input_2) + biases['output']
    a = sigmoid(z)
    return z, a

反向传播

首先计算输出层
根据$${\delta }^{[L]}=\frac{\partial L}{\partial a^{[L]}}\odot {\sigma }^{\prime }(z^{[L]})$$
我们先要计算$\frac{\partial L}{\partial a^{[L]}}$,由于$L(a^{[L]},y)=\frac{1}{2n}\sum _{i=1}^n(y^{(i)}-a^{[L](i)}{)}^2$所以：
$\frac{\partial L}{\partial a^{[L]}}=\frac{1}{n}\sum _{i=1}^n(a^{[L](i)}-y^{(i)})$
这里需要注意，反向传播原理是链式法则，所以这里应该是
$${\delta }^{[L]}=\frac{\partial L}{\partial a^{[L]}}\odot {\sigma }^{\prime }(z^{[L]})=\frac{1}{n}\sum _{i=1}^n[(a^{[L](i)}-y^{(i)}){\sigma }^{\prime }(z^{[L](i)})]$$
而不是
$${\delta }^{[L]}=\frac{\partial L}{\partial a^{[L]}}\odot {\sigma }^{\prime }(z^{[L]})=\frac{1}{n}\sum _{i=1}^n[(a^{[L](i)}-y^{(i)})]{\sigma }^{\prime }(z^{[L]})$$
所以我们先计算链式法则的部分，不着急求和
然后计算隐藏层的$\delta$
$${\delta }^{[l]}=W^{[l+1{]}^T}\cdot {\delta }^{[l+1]}\odot {\sigma }^{\prime }(z^{[l]})$$
可以直接套入计算
最后是算各个的偏导
$$\begin{gathered} \nabla \frac{\partial L}{\partial b^{[l]}}={\delta }^{[l]} \\ \nabla \frac{\partial L}{\partial w^{[l]}}={\delta }^{[l]}\cdot a^{l-1^T} \end{gathered}$$
此时就可以求和了，因为链式法则的部分已经结束。

# backpropagation
def bp(X, y):
    z_1, a_1 = forward_1(X)
    z_2, a_2 = forward_2(a_1)
    z_3, a_3 = forward_3(a_2) # 输出

    size = X.shape[1]
    delta_3 = (a_3 - y) * d_sigmoid(z_3) # 计算各个delta
    delta_2 = np.dot(weights['output'].T, delta_3) * sigmoid(z_2)
    delta_1 = np.dot(weights['W2'].T, delta_2) * sigmoid(z_1)
    
    
    w_1 = np.dot(delta_1, X.T) / size # 计算梯度
    b_1 = np.sum(delta_1, axis=1).reshape(-1, 1) / size
    w_2 = np.dot(delta_2, a_1.T) / size
    b_2 = np.sum(delta_2, axis=1).reshape(-1, 1) / size
    w_3 = np.dot(delta_3, a_2.T) / size
    b_3 = np.sum(delta_3, axis=1).reshape(-1, 1) / size
    loss = np.sum((a_3 - y) ** 2) / (size * 2) # 计算代价函数的值
    return w_1, b_1, w_2, b_2, w_3, b_3, loss

值的说的是，在计算w时不需要求和，因为矩阵运算时已经求过了。

梯度下降

然后就是熟悉的梯度下降法了

def gd(X, y, eps=0.8, iter=300000):# eps就是学习率，iter为最大迭代次数
    cnt = 1
    cc = None
    while True:
        if cnt > iter: break
        w_1, b_1, w_2, b_2, w_3, b_3, loss = bp(X, y)
        cc = loss
        weights['W1'] -= w_1 * eps
        weights['W2'] -= w_2 * eps
        weights['output'] -= w_3 * eps
        biases['B1'] -= b_1 * eps
        biases['B2'] -= b_2 * eps
        biases['output'] -= b_3 * eps
        cnt += 1
        if loss < 0.01:
            break
    print('loss = ', cc)

最后再额外计算一个score，使用ACC的标准

a = forward(data)
a[a > 0.5] = 1
a[a <= 0.5] = 0
print('acc = ', np.sum(a == target) / len(target))

把所有的合起来就是

import numpy as np 
import matplotlib.pyplot as plt 

# constants
n_input = 2
hid_layer_1 = 3
hid_layer_2 = 2
n_output = 1
# init parameters
np.random.seed(666)
weights = {
    'W1': np.random.normal(size=(hid_layer_1, n_input)),
    'W2': np.random.normal(size=(hid_layer_2, hid_layer_1)),
    'output': np.random.normal(size=(n_output, hid_layer_2))
}
biases = {
    'B1': np.random.normal(size=(hid_layer_1, 1)),
    'B2': np.random.normal(size=(hid_layer_2, 1)),
    'output': np.random.normal(size=(n_output, 1))
}
# activation function
def sigmoid(X):
    return 1 / (np.exp(-X) + 1)

def d_sigmoid(X):
    tmp = sigmoid(X)
    return tmp * (1 - tmp)

# forward propagation
def forward(X):
    h1 = sigmoid(np.dot(weights['W1'], X) + biases['B1'])
    h2 = sigmoid(np.dot(weights['W2'], h1) + biases['B2'])
    output = sigmoid(np.dot(weights['output'], h2) + biases['output'])
    return output

def forward_1(input_0):
    z = np.dot(weights['W1'], input_0) + biases['B1']
    a = sigmoid(z)
    return z, a

def forward_2(input_1):
    z = np.dot(weights['W2'], input_1) + biases['B2']
    a = sigmoid(z)
    return z, a

def forward_3(input_2):
    z = np.dot(weights['output'], input_2) + biases['output']
    a = sigmoid(z)
    return z, a


# backpropagation
def bp(X, y):
    z_1, a_1 = forward_1(X)
    z_2, a_2 = forward_2(a_1)
    z_3, a_3 = forward_3(a_2) # 输出

    size = X.shape[1]
    delta_3 = (a_3 - y) * d_sigmoid(z_3) # 输出
    delta_2 = np.dot(weights['output'].T, delta_3) * sigmoid(z_2)
    delta_1 = np.dot(weights['W2'].T, delta_2) * sigmoid(z_1)
    
    
    w_1 = np.dot(delta_1, X.T) / size
    b_1 = np.sum(delta_1, axis=1).reshape(-1, 1) / size
    w_2 = np.dot(delta_2, a_1.T) / size
    b_2 = np.sum(delta_2, axis=1).reshape(-1, 1) / size
    w_3 = np.dot(delta_3, a_2.T) / size
    b_3 = np.sum(delta_3, axis=1).reshape(-1, 1) / size
    loss = np.sum((a_3 - y) ** 2) / (size * 2)
    return w_1, b_1, w_2, b_2, w_3, b_3, loss

def gd(X, y, eps=2, iter=30000):
    cnt = 1
    cc = None
    while True:
        if cnt > iter: break
        w_1, b_1, w_2, b_2, w_3, b_3, loss = bp(X, y)
        cc = loss
        weights['W1'] -= w_1 * eps
        weights['W2'] -= w_2 * eps
        weights['output'] -= w_3 * eps
        biases['B1'] -= b_1 * eps
        biases['B2'] -= b_2 * eps
        biases['output'] -= b_3 * eps
        cnt += 1
        if loss < 0.01:
            break
    print('loss = ', cc)



from sklearn import datasets

iris = datasets.load_iris()
data = iris['data'][:, [1, 3]].T
target = iris['target']
target[target == 2] = 1

gd(data, target)
a = forward(data)
a[a > 0.5] = 1
a[a <= 0.5] = 0
print('acc = ', np.sum(a == target) / len(target))

最后附一个结果

如果继续训练下去loss会继续减小，但是速度会越来越慢，这与激活函数sigmoid有一定的关系。

Tips for training

在深度学习中，应该先看训练出的模型在训练集上的效果，然后再看在测试集上的效果。有可能训练出的模型在训练集上就不好。这一点与传统机器学习不同

梯度消失

假设有这么一个前馈网络

我们想要求$\frac{\partial C}{\partial w_1}$就可以根据反向传播来求，设第$i$个神经元中，前向传播的计算过程为$z_1=W_i{a}_{i-1}+b_1,a=\sigma (z_i)$其中$\sigma (x)=\frac{1}{1+e^{-x}}$
那么就可以得到$\frac{\partial C}{\partial w_1}=\frac{\partial C}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_1}$
求出后就是$\frac{\partial C}{\partial w_1}=\frac{\partial C}{\partial a_3}{\sigma }^{\prime }(z_3)w_3{\sigma }^{\prime }(z_3)w_2{\sigma }^{\prime }(z_1)x_1$。而Sigmoid的导数长这个样子。
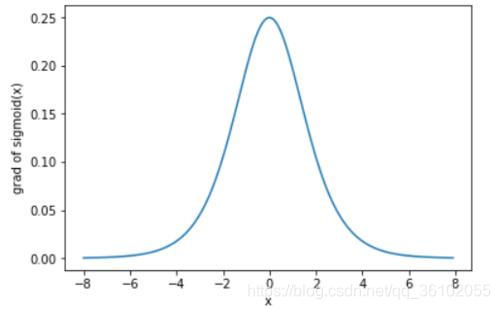
最大时也就$\frac{1}{4}$，而且我们初始化参数时通常也会初始化很小，也就是w的值会很小。
当隐藏层多起来时，问题就出现了此时就会有大量的$\sigma (z_i)w_i$相乘，基本每个$|\sigma (z_i)w_i|<0.25$他们相乘起来就会导致梯度消失发生，而当$|\sigma (z_i)w_i|>1$时就会导致梯度爆炸发生，两种情况都有可能会使梯度下降法下降到某一个过程就停止了。

想要改变这一状况，一个方法就是改变激活函数。

激活函数

激活函数对于神经网络是一个重要的东西，如果没有一个非线性的激活函数，那么神经网络就会退化成一个线性函数。

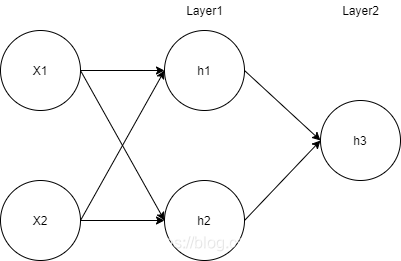
设Layer1的权重，截距(或者说偏移)为$W^1,b^1$，Layer2为$W^2,b^1=2$激活函数为$\sigma (x)$
假设没有激活函数。
那么
$z_1=W^{1}x+b^1$
$a_1=z_1$
$z_2=W^2{a}_1+b^2$
$z_2=W^1{W}^{2}x+W^1{b}^1+b^2$
设$W^1{W}^2=W^{\ast },W^1{b}^1+b^2=b^{\ast }$
则可以得到
$z_2=W^{\ast }x+b^{\ast }$
此时输出
$a_2=z_2=W^{\ast }x+b^{\ast }$
可以发现，他就是个各个特征之间的线性组合，这样做就失去了使用深度学习的意义。
假设我们使用非线性激活函数，就会得到一个线性的模型，那么此时
$z_1=W^{1}x+b^1$
$a_1=\sigma (z_1)$
$z_2=W^2{a}_1+b^2$
此时输出
$a_2=z_2=\sigma [W^2\sigma (W^{1}x+b^1)+b^2]$由于$\sigma (x)$是非线性的，所以最终的结果和各个特征之间的也是非线性的关系。
那么非线性的函数很多，通常都有哪些作为激活函数呢。

1. Sigmoid函数
   
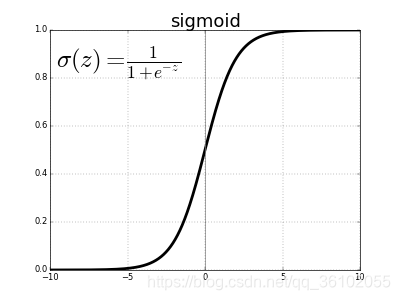
   他可以把实数范围内的值映射到$0-1$之间，在逻辑回归中被使用过。
   Sigmoid函数有很多缺点，上面的梯度消失就是其中一种，还有的就是使用Sigmoid函数它的输出是在$(0,1)$给下一层的输入的均值就不是处于0了，再有的就是

2. Tanh函数
   Tanh就是高数书上讲的双曲正切函数
   
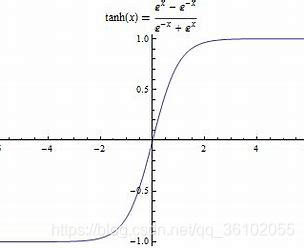
   它的值域到了$(-1,1)$之间，解决了均值中心问题，但是依然无法解决梯度消失问题。

3. ReLu函数
   ReLu函数也叫线性整流函数，他是一个分段函数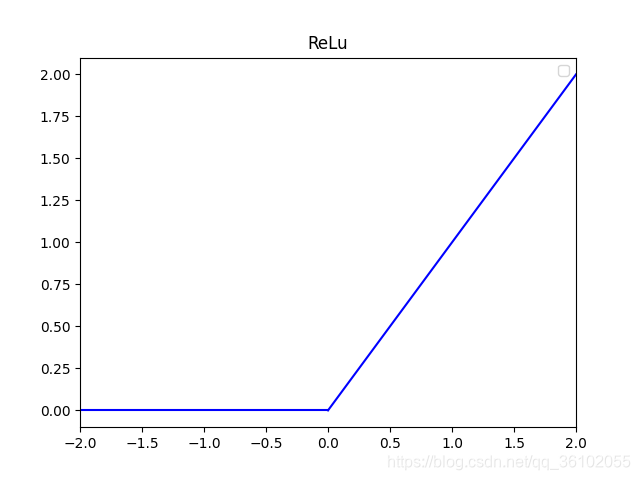
   它的函数解析式就是$f(x)=\{\begin{array}{ll}0& \text{x}\le 0\\ x& \text{x}>0\end{array}$这个函数可以解决上述梯度消失的问题，因为在可求导的区域内，它的导数要么是0要么是1，不会在反向传播时产生累计影响，并且它的运算比上述的函数都要快。
   注意，虽然看起来可能会使最终的模型变成线性函数，但其实并不是。
   
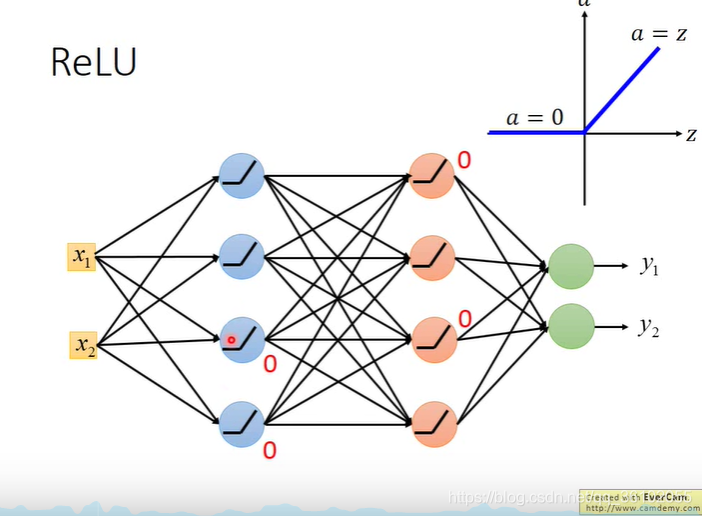
   如下图，在输入某个值后有一些变神经元的输出为0，那么他们就相当于不会对后面的神经元产生影响。
   
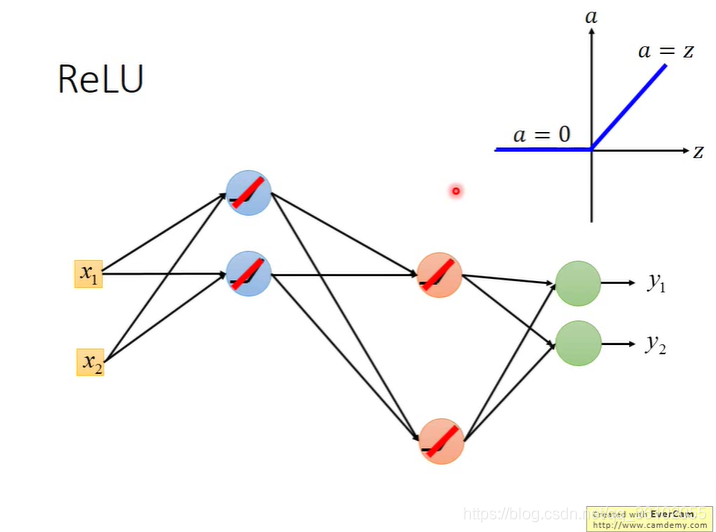
   于是神经网络就变成了这样，但是此时看起来就变成了了一个线性模型，但其实并不是，对于这个输入得到的确实是，但是随着输入的变化，整个网络的"结构"也会变化，有一些又会变成0，有一些又会变回线性，所以对于整体的模型它依然是非线性的。

4. Leaky ReLu
   由于ReLU它的负数部分导数为零，后面就不会总成影响，于是就有人想能不能加上一点斜率呢，于是就有Leaky ReLu。

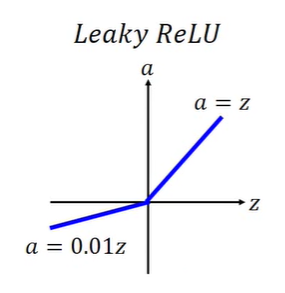
但是这样不够，凭什么，斜率是0.01呢，于是就有了进一步的带参数的ReLU

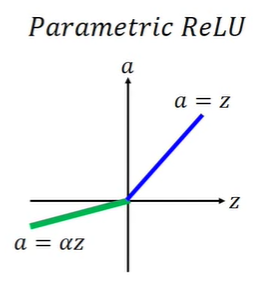
其中x负方向的斜率是一个可学习的参数$\alpha$，可以通过梯度下降法学来。

5. MaxOut
   MaxOut则是一种更进一步的想法，它可以自己去进行学习激活函数，而ReLu函数就是其中的一个一个特列。
   
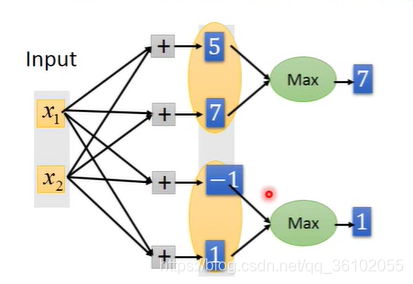
   MaxOut的做法首先是分组，上图中黄色区域内的神经元是一组，这个组是要事先决定好的，然后这一组再当成一个独立的节点，这个节点的输出等于这一组内的节点输出的的最大值，也就是对组内所有输出取max。
   
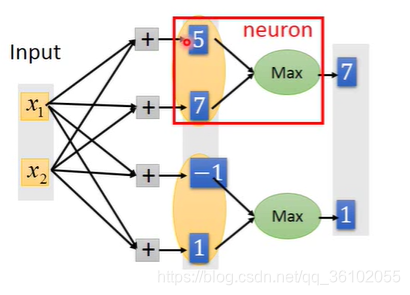
   而对于每一组内部的节点其本身的运算得到的结果就是一个线性的函数(内部节点没有激活函数，只进行乘以权值求和，也就是所有"特征"的线性组合)而对他们去max就是把这些函数截成若干段，于是就得到一个属于这个组的激活函数。

Adaptive Learning rate(自适应学习率)

Adagrad

梯度下降法中每次都朝着梯度的反方向进行前进，每次前进都会乘以一个参数$\eta$表示每次前进的距离。但是由于各个地方的梯度不一样，所以每个地方不能都前进固定的距离，所以就需要一个可以自主进行改正的距离。

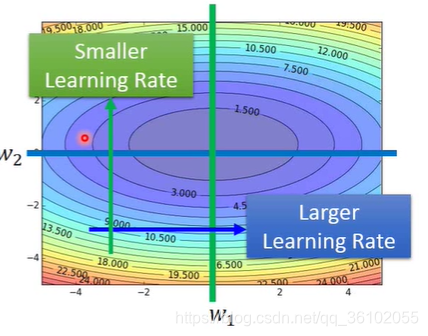
同时我们在前进的过程中，逐渐接近目标点，每次前进的距离也应该越来越小，不然可能越过目标点，所以一种解决这种问题的方法就是对以前的梯度进行累计求和，然后再除去

上图中$w$是权重，$\eta$是学习率$g^i$是第i次求得的梯度。
这样，越接近终点，前进的距离就会越小，同时在梯度比较小的地方前进的距离就比较打，梯度大的地方反之。
但是这样的变化速度依然比较慢，因为是累计求和，所以新得到的梯度起的决定作用是越来越小的，于是就有了RMSProp

RMSProp

RMSProp的做法是这样的

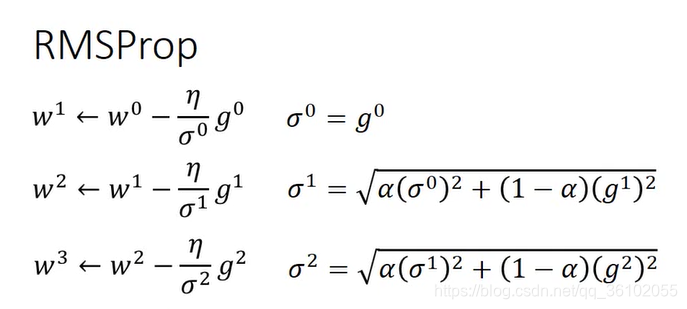
即每次算的是之前梯度和当前计算出梯度的平方加权和开根号，$\alpha$越大则越倾向于以前的梯度，小则倾向于相信新算出的梯度。
这里有一篇博客讲RMSProp和其他的几个最优化的算法都讲的很好，可以去看看 这里

Local Minimum(局部最优解)

在进行梯度下降时，有可能会卡在一些地方，比如局部最小指点，鞍点，甚至是非常平缓的区域

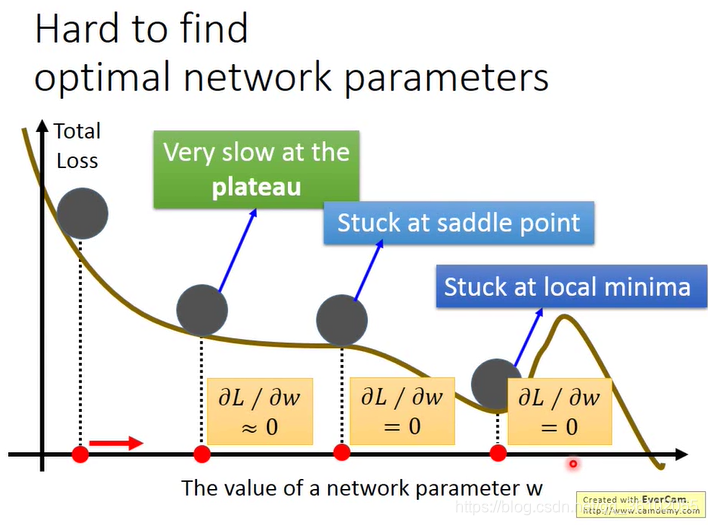
Momentum

Momentum是模拟了现实世界中物体运动规律的算法，在现实世界中，物体运动总是带有一定的惯性，Momentum就是模拟了这个惯性。
假设${\theta }_i$为第$i$次计算出的梯度$v_i$表示第i次的前进方向。则
$v_1=\eta {\theta }_1$
$v_2=\lambda v_1+\eta {\theta }_2$
$v_3=\lambda v_2+\eta {\theta }_3$
…
每次都是由惯性的方向和当前梯度的方向进行矢量合成，其中$\lambda$用于控制惯性的影响程度
由于有了惯性，所以到达一个局部最优解后，有可能会冲出这个局部最优解，从而找到全局最优解。

Drop Out

Drop Out可以解决过拟合问题
Drop Out的大概操作如下：

1. 对整个network中的隐藏层神经元进行抽取，每个神经元都有$(1-p\%)$的几率被抽中。
2. 把没被抽中的神经元暂时去掉，并且与之的连线也去掉，然后对剩下的网络进行一次梯度下降，并且对没有被去掉的神经元进行更新参数。
3. 恢复上一次被去掉的神经元，并且重新执行1,2

如此重复多次。
最后得到的网络是完整的，也就是不缺少神经元，但是所有的权重W都要乘(1-p)，这样可以与训练时的输出大小规模相匹配。
Drop Out的原理可以看做是一种集成学习中voting的思想。